“Layered Reconstruction of Stippling Art” by Parakkat, Memari and Cani
Conference:
Type(s):
Entry Number: 17
Title:
- Layered Reconstruction of Stippling Art
Presenter(s)/Author(s):
Abstract:
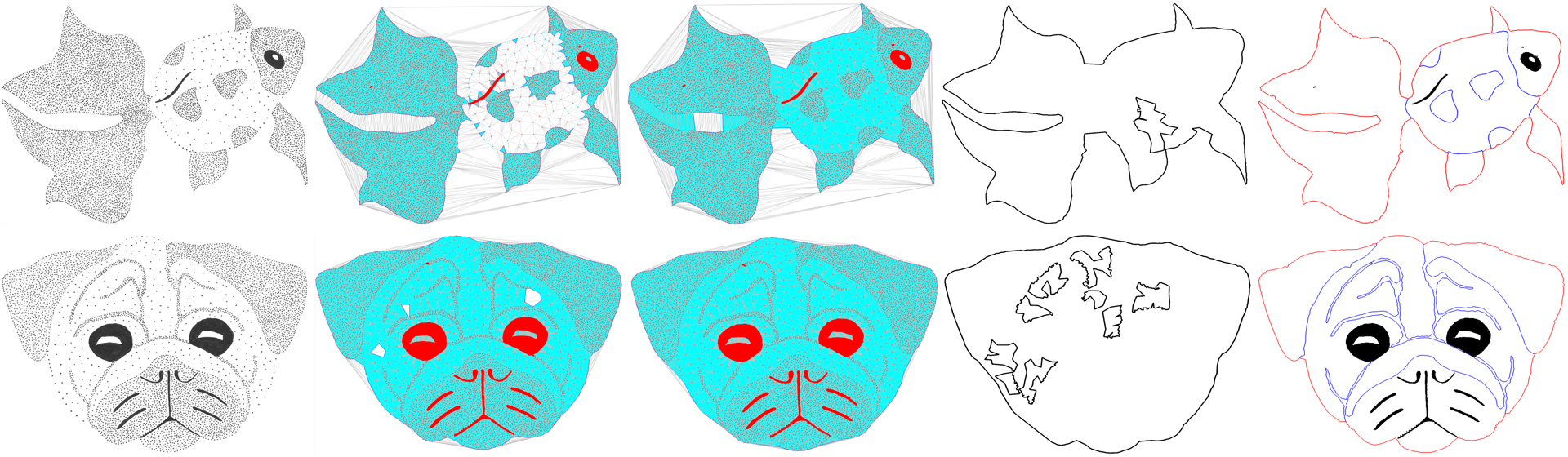
Given a point set S ⊆ R 2 , reconstruction refers to the process of identifying a vector shape that best approximates the input. Although this field was pioneered since 1983 by Edelsbrunner [Edelsbrunner et al. 2006] and has been heavily studied since then, the general problem still remains open, ill-posed and challenging. Solving it is essential for a wide range of applications, from image processing, pattern recognition and sketching to wireless networks. The main motivation of our work is extend reconstruction to the case of stippled art (for eg. Hedcut drawings), as well as finding an inverse to the well studied problem of image conversion to blue noise (see for instance deGoes et al. [de Goes et al. 2012]). Solution to this problem is extremely difficult since we expect reconstruction to be consistent with human cognition and perception of the art piece, while possible feature extraction heavily depends on various parameters of the input point set (density, distribution etc). In this work, we introduce a dedicated variant of traditional 2D reconstruction in which the input point set (a stippled image) can include different regions corresponding to different point densities.
Our method converts this input into a layered, vector representation, which includes a main shape plus internal, closed regions, defined by their boundary. Providing such structured output eases subsequent editing and processing, such as generating shaded vector images from the stippled input [Orzan et al. 2008]. To achieve this, we first apply a layered reconstruction algorithm based on the detected regions in the input point set, and use the output for generating the outer and inner shape boundaries in the stippled drawing.
References:
- Fernando de Goes, Katherine Breeden, Victor Ostromoukhov, and Mathieu Desbrun. 2012. Blue Noise Through Optimal Transport. ACM Trans. Graph. 31, 6, Article 171 (Nov. 2012), 11 pages.
- Matt Duckham, Lars Kulik, Mike Worboys, and Antony Galton. 2008. Efficient generation of simple polygons for characterizing the shape of a set of points in the plane. Pattern Recognition 41, 10 (2008), 3224 – 3236.
- Edelsbrunner, D. Kirkpatrick, and R. Seidel. 2006. On the Shape of a Set of Points in the Plane. IEEE Trans. Inf. Theor. 29, 4 (Sept. 2006), 551–559.
- Subhasree Methirumangalath, Shyam Sundar Kannan, Amal Dev Parakkat, and Ramanathan Muthuganapathy. 2017. Hole detection in a planar point set: An empty disk approach. Computers Graphics 66 (2017), 124 – 134. Shape Modeling International 2017.
- Subhasree Methirumangalath, Amal Dev Parakkat, and Ramanathan Muthuganapathy. 2015. A unified approach towards reconstruction of a planar point set. Computers Graphics 51 (2015), 90 – 97. Conference Shape Modeling International.
- Alexandrina Orzan, Adrien Bousseau, Holger Winnemöller, Pascal Barla, Joëlle Thollot, and David Salesin. 2008. Diffusion Curves: A Vector Representation for SmoothShaded Images. In ACM Transactions on Graphics (Proceedings of SIGGRAPH 2008), Vol. 27.
- Amal Dev Parakkat and Ramanathan Muthuganapathy. 2016. Crawl Through Neighbors: A Simple Curve Reconstruction Algorithm. In Proceedings of the Symposium on Geometry Processing (SGP ’16). 177–186.