“Interactive Boolean operations for conceptual design of 3-D solids” by Rappoport and Spitz

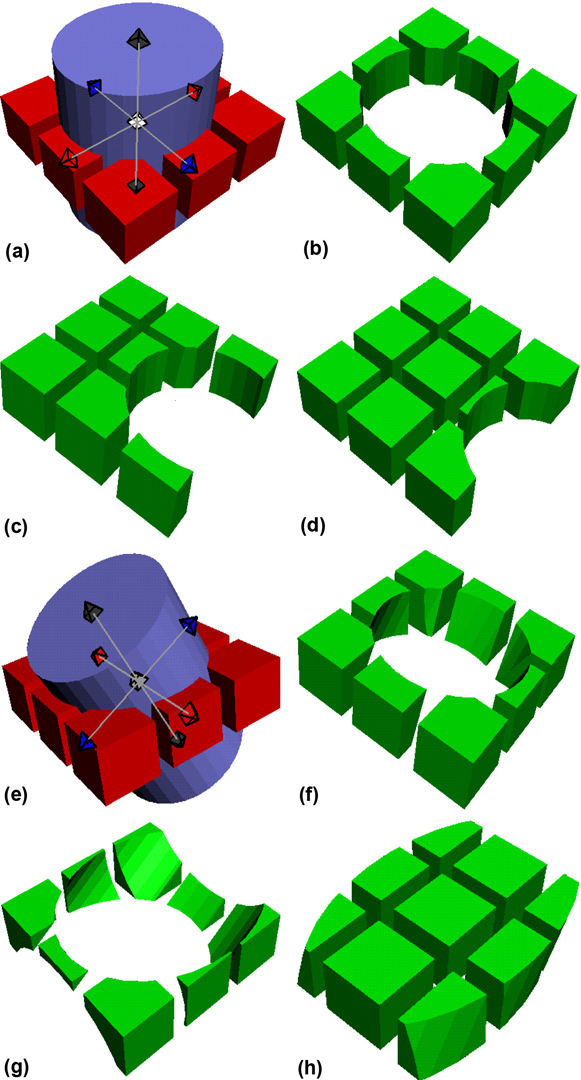
Interactive modeling of 3-D solids is an important and difficult problem in computer graphics. The Constructive Solid Geometry (CSG) modeling scheme is highly attractive for interactive design, due to its support for hierarchical modeling and Boolean operations. Unfortunately, current algorithms for interactive display of CSG models require expensive special-purpose hardware that is not easily available. In this paper we present a method for interactive display of CSG models using standard, widely available graphics hardware. The method enables the user to interactively modify the affine transformations associated with CSG sub-objects. The application we focus upon is that of conceptual design, a stage in the design process in which rapid, interactive visualization of the model and high-level design operations are of crucial importance, while the objects are relatively simple. The method converts the CSG graph to a novel Convex Differences Aggregate(CDA) representation. The CDA utilizes graph re-writing techniques, efficient geometric algorithms on convex objects and a built-in hierarchical acceleration scheme. The CDA rendering algorithm is very simple, takes advantage of standard graphics hardware, and makes efficient use of system resources by splitting the work between the graphics system and the CPU.

1. Atherton, RR., A scan-line hidden surface removal procedure for constructive solid geometry. Computer Graphics, 17(3):73- 82, 1983 (Siggraph ’83).
2. Barber, C.B., Dobkin, D.R, Huhdanpaa, H.T., The Quickhull algorithm for convex hull, GCG53, The Geometry Center, Minneapolis, 1993 (ftp.geom.umn.edu/pub/software/qhull.tar.Z).
3. Batchelor, B.G., Hierarchical shape description based upon convex hulls of concavities. J. of Cybernetics, 10:205-210, 1980.
4. Bieri, H., Nef, W., Elementary set operations with d-dimensional polyhedra. Computational Geometry and its Applications, LNCS 333, Springer-Verlag, 1988, pp. 97-112.
5. Breen, D.E., Constructive cubes: CSG evaluation for display using discrete 3-D scalar data sets. Eurographics ‘91,127-142, 1991.
6. Bronsvoort, W.F., An algorithm for visible-line and visible-surface display of CSG models. The Visual Computer, 3:176- 185, 1987.
7. Cameron, S.A., Direct drawing from CSG models with hidden-line removal. CSG 94, Set-Theoretic Solid Modeling: Techniques and Applications, Information Geometers, 1994, pp. 179-192.
8. Chazelle, B., Dobkin, D., Intersection of convex objects in two and three dimensions, Journal of the ACM, 34(1): 1-27, 1987.
9. Chazelle, B., An optimal algorithm for intersecting threedimensional convex polyhedra. SlAM J. Comput., 21(4):671-696, 1992.
10. Dobkin, D.E, Kirkpatrick, D.G., Fast detection of polyhedral intersection. Theoret. Comput. Sci., 27:241-253, 1983.
11. Emmerik, M.J.G.M. van, Rappoport, A., Rossignac, J., Simplifying interactive design of solid models: a hypertext approach. The Visual Computer, 9:239-254, 1993.
12. Goldfeather, J., Hultquist, J.EM., Fuchs, H., Fast constructive solid geometry display in the pixel-power graphics system. Computer Graphics, 20(4):107-116, 1986 (Siggraph ’86).
13. Goldfeather, J., Molnar, S., Turk, G., Fuchs, H., Near realtime CSG rendering using tree normalization and geometric pruning. IEEE CG&A, 9:20-28, May 1989.
14. Hertel, S., M~intyl~i, M., Mehlhorn, K., Nievergelt, J., Space sweep solves intersection of convex polyhedra. Acta Inform., 21:501- 519, 1984.
15. Hoffmann, C., Geometric and Solid Modeling: an Introduction. Morgan Kaufmann, 1989.
16. Kim, Y.S., Convex decomposition and solid geometric modeling. Ph.D. Thesis, Mech. Eng., Stanford University, 1990.
17. Jansen, F.W., A pixel-parallel hidden surface algorithm for constructive solid geometry. Eurographics ’86, Elsevier Science, NY, 29-40, 1986.
18. Jansen, F.W., CSG hidden surface algorithms for VLSI hardware systems. In: Advances in Computer Graphics Hardware I, Springer-Verlag, 1987, pp. 75-82.
19. Jansen, F.W., Depth-order point classification techniques for CSG display algorithms, ACM Trans. on Graphics, 10(1):40-70, 1991.
20. Meagher, D.J., Interactive solids processing for medical analysis and planning. Computer Graphics ’84, NCGA Conference Proceedings, vol. 2, NCGA, 1984, pp. 96-106.
21. McReynolds, T., Blythe, D., Programming with OpenGL: Advanced Rendering, course #23, Siggraph ’96, pp. 36-40.
22. Muller, D.E., Preparata, F.E, Finding the intersection of two convex polyhedra. Theoret. Comput. Sci., 7:217-236, 1978.
23. Naylor, B., Interactive solid modeling using partitioning trees. Graphics Interface ’92, pp. 11-18.
24. Naylor, B., Destructive solid geometry for interactive entertainment and training, CSG 96, Cambridge, UK, 1996.
25. Okino, N., Kakazu, Y., Moritomo, M., Extended depth-buffer algorithms for hidden-surface visualization. IEEE CG&A, 4:79-88, 1984.
26. Ponamgi, M., Manocha, D., Lin, M.C., Incremental algorithms for collision detection between solid models. Proceedings, 3rd ACM/Siggraph Symposium on Solid Modeling and Applications (Solid Modeling ’95), ACM Press, 1995, pp. 293-304.
27. Preparata, F., Shamos, M. I., Computational Geometry: An Introduction, Springer-Verlag, New-York, 1985.
28. Rappoport, A., Using convex differences in hierarchical representations of polygonal maps. Graphics Interface ’90, pp. 183- 189.
29. Rappoport, A., The extended convex differences tree (ECDT) representation for n-dimensional polyhedra. Intl. J. Cornput. Geom. and App., 1(3):227-241, 1991. Also: proceedings, ACM/Siggraph Symposium on Solid Modeling Foundations and CAD~CAM Applications (Solid Modeling ’91), ACM Press, 1991, pp. 139-148.
30. Rappoport, A., An efficient adaptive algorithm for constructing the convex differences tree of a simple polygon. Computer Graphics Forum, 11(4):235-240, 1992.
31. Rappoport, A., Geometric modeling: a new fundamental framework and its practical implications. Proceedings, 3rd ACM/Siggraph Symposium on Solid Modeling and Applications (Solid Modeling ’95), ACM Press, 1995, pp. 31-42.
32. Rappoport, A., Breps as displayable-selectable models in interactive design of families of geometric objects. Theory and Practice of Geometric Modeling (Blaubeuren II), Ttibingen, Germany, October 1996. Proceedings to be published by Springer-Veflag.
33. Rappoport, A., The Generic Geometric Complex: a modeling scheme for families of decomposed pointsets. Proceedings, 4th ACM/Siggraph Symposium on Solid Modeling and Applications (Solid Modeling ’97), ACM Press, 1997, pp. 31-4 1.
34. Requicha, A.G., Representations for rigid solids: Theory, methods and systems. ACM Computing Surveys, 12:437-464, 1980.
35. Requicha, A.G., Voelcker, H.B., Boolean operations in solid modeling: boundary evaluation and merging algorithms, Proc. of the IEEE 73(1):30-44, 1985.
36. Rossignac, J.R., Requicha, A.A.G., Depth-buffering display techniques for constructive solid geometry. IEEE CG&A, 6:29- 39, Sep. 1986.
37. Rossignac, J.R., Wu, J., Correct shading of regularized CSG solids using a depth-interval buffer. In: Grimsdale, R.L., Kaufman, A., (eds), Advances in Computer Graphics Hardware V, Springer-Verlag, Berlin, 1990, pp. 117-138.
38. Rossignac, J.R., Processing disjunctive forms directly from CSG graphs. CSG 94, Set-Theoretic Solid Modeling: Techniques and Applications, Information Geometers, 1994, pp. 55-70.
39. Roth, S.D., Ray casting for modeling solids. CVGIP, 18(2):109- 144, 1982.
40. Sklansky, J., Measuring concavity on a rectangular mosaic. tEEE Tran. Com., 21:1355-1364, 1972.
41. Smithers, T., AI-based design versus geometry-based design, or why design cannot be supported by geometry alone. Computer- Aided Design, 21(3):141-150, 1989.
42. Spitz, S., Interactive Boolean operations and collision detection on polyhedral solids. Amirim project report, Institute of Computer Science, The Hebrew University, July 1994.
43. Thibault, W.C., Naylor, B.F., Set operations on polyhedra using binary space partitioning trees. Computer Graphics, 21(4):153- 162, 1987 (Siggraph ’87).
44. Tor, S.B., Middleditch A.E., Convex decomposition of simple polygons. ACM Trans. on Graphics, 3(4):244-265, 1984.
45. Van Hook, T., Real-time shaded NC milling display. Computer Graphics, 20(4): 15-20, 1986 (Siggraph ’86).
46. Wiegand, T.F., Interactive rendering of CSG models. Computer Graphics Forum, 15(4):249-261, 1996.
47. Woo, T., Feature extraction by volume decomposition. Technical Report 82-4, Dept. of Indus. and Oper. Eng., The University of Michigan, 1982.