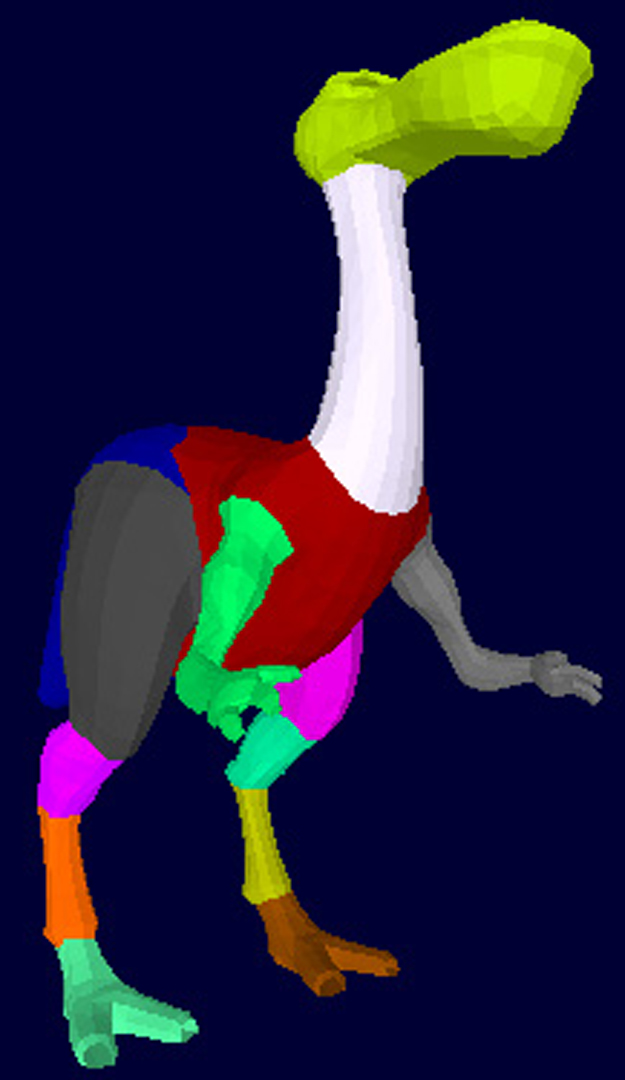
“Hierarchical mesh decomposition using fuzzy clustering and cuts” by Katz and Tal

Cutting up a complex object into simpler sub-objects is a fundamental problem in various disciplines. In image processing, images are segmented while in computational geometry, solid polyhedra are decomposed. In recent years, in computer graphics, polygonal meshes are decomposed into sub-meshes. In this paper we propose a novel hierarchical mesh decomposition algorithm. Our algorithm computes a decomposition into the meaningful components of a given mesh, which generally refers to segmentation at regions of deep concavities. The algorithm also avoids over-segmentation and jaggy boundaries between the components. Finally, we demonstrate the utility of the algorithm in control-skeleton extraction.

1. BIEDERMAN, I. 1987. Recognition-by-components: A theory of human image understanding. Psychological Review 94, 115–147.Google ScholarCross Ref
2. BLOOMENTHAL, J., AND LIM, C. 1999. Skeletal methods of shape manipulation. In International Conference on Shape Modeling and Applications, 44–49. Google Scholar
3. CHAZELLE, B., AND PALIOS, L. 1992. Decomposing the boundary of a nonconvex polyhedron. In SWAT, 364–375. Google Scholar
4. CHAZELLE, B., AND PALIOS, L. 1994. Decomposition algorithms in geometry. In Algebraic Geometry and its Applications, Springer-Verlag, C. C. Bajaj, Ed., Ed., 419–447.Google Scholar
5. CHAZELLE, B., DOBKIN, D., SHOURHURA, N., AND TAL, A. 1997. Strategies for polyhedral surface decomposition: An experimental study. Computational Geometry: Theory and Applications 7, 4–5, 327–342. Google ScholarDigital Library
6. CORMEN, T., LEISERSON, C., RIVEST, R., AND STEIN, C. 2001. Introduction to Algorithms. McGraw-Hill. Google Scholar
7. DUDA, R., AND HART, P. 1973. Pattern Classification and Scene Analysis. New-York, Wiley.Google Scholar
8. GAGVANI, N., KENCHAMMANA-HOSEKOTE, D., AND SILVER, D. 1998. Volume animation using the skeleton tree. In IEEE Symposium on Volume Visualization, 47–53. Google Scholar
9. GARLAND, M., AND HECKBERT, P. 1997. Surface simplification using quadric error metrics. In Proceedings of SIGGRAPH 1997, 209–216. Google ScholarDigital Library
10. GARLAND, M., WILLMOTT, A., AND HECKBERT, P. 2001. Hierarchical face clustering on polygonal surfaces. In Proceedings of ACM Symposium on Interactive 3D Graphics, 49–58. Google Scholar
11. GOLDBERG, A., AND TARJAN, R. 1988. A new approach to the maximum flow problem. Journal of the ACM 35, 4, 921–940. Google ScholarDigital Library
12. GREGORY, A., STATE, A., LIN, M., MANOCHA, D., AND LIVINGSTON, M. 1999. Interactive surface decomposition for polyhedral morphing. The Visual Computer 15, 453–470.Google ScholarDigital Library
13. KARNI, Z., AND GOTSMAN, C. 2000. Spectral compression of mesh geometry. In Proceedings of SIGGRAPH 2000, ACM SIGGRAPH, 279–286. Google ScholarDigital Library
14. LAZARUS, F., AND VERROUST, A. 1999. Level set diagrams of polyhedral objects. In ACM Symposium on Solid Modeling and Applications, 130–140. Google Scholar
15. LEVY, B., PETITJEAN, S., RAY, N., AND MAILLOT, J. 2002. Least squares conformal maps for automatic texture atlas generation. In Proceedings of SIGGRAPH 2002, ACM SIGGRAPH, 362–371. Google ScholarDigital Library
16. LEWIS, J., CORDNER, M., AND FONG, N. 2000. Pose space deformations: A unified approach to shape. In Proceedings of SIGGRAPH 2000, ACM SIGGRAPH, 165–172. Google Scholar
17. LI, X., TOON, T., TAN, T., AND HUANG, Z. 2001. Decomposing polygon meshes for interactive applications. In Proceedings of the 2001 symposium on Interactive 3D graphics, 35–42. Google Scholar
18. MANGAN, A., AND WHITAKER, R. 1999. Partitioning 3D surface meshes using watershed segmentation. IEEE Transactions on Visualization and Computer Graphics 5, 4, 308–321. Google ScholarDigital Library
19. SHARON, E., BRANDT, A., AND BASRI, R. 2000. Fast multiscale image segmentation. In Proceedings IEEE Conference on Computer Vision and Pattern Recognition, 70–77.Google ScholarCross Ref
20. SHI, J., AND MALIK, J. 2000. Normalized cuts and image segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence 22, 8, 888–905. Google ScholarDigital Library
21. SHINAGAWA, Y., KUNII, T., AND KERGOSIEN, Y. 1991. Surface coding based on morse theory. IEEE Computer Graphics and Applications 11, 5, 66–78. Google ScholarDigital Library
22. SHLAFMAN, S., TAL, A., AND KATZ, S. 2002. Metamorphosis of polyhedral surfaces using decomposition. In Eurographics 2002, 219–228.Google Scholar
23. TEICHMANN, M., AND TELLER, S. 1998. Assisted articulation of closed polygonal models. In Conference abstracts and applications: SIGGRAPH, ACM SIGGRAPH, 14–21. Google Scholar
24. WADE, L., AND PARENT, R. 2002. Automated generation of control skeletons for use in animation. The Visual Computer 18, 2, 97–110.Google ScholarDigital Library
25. WEBER, J. 2000. Run-Time Skin Deformation. Intel Architecture Labs, www.intel.com.Google Scholar
26. WU, Z., AND LEAHY, R. 1993. An optinal graph theoretic approach to data clustering: Theory and its application to image segmentation. PAMI 11, 1101–1113. Google ScholarDigital Library
27. ZOCKLER, M., STALLING, D., AND HEGE, H.-C. 2000. Fast and intuitive generation of geometric shape transitions. The Visual Computer 16, 5, 241–253.Google ScholarCross Ref
28. ZUCKERBERGER, E., TAL, A., AND SHLAFMAN, S. 2002. Polyhedral surface decomposition with applications. Computers & Graphics 26, 5, 733–743.Google ScholarCross Ref