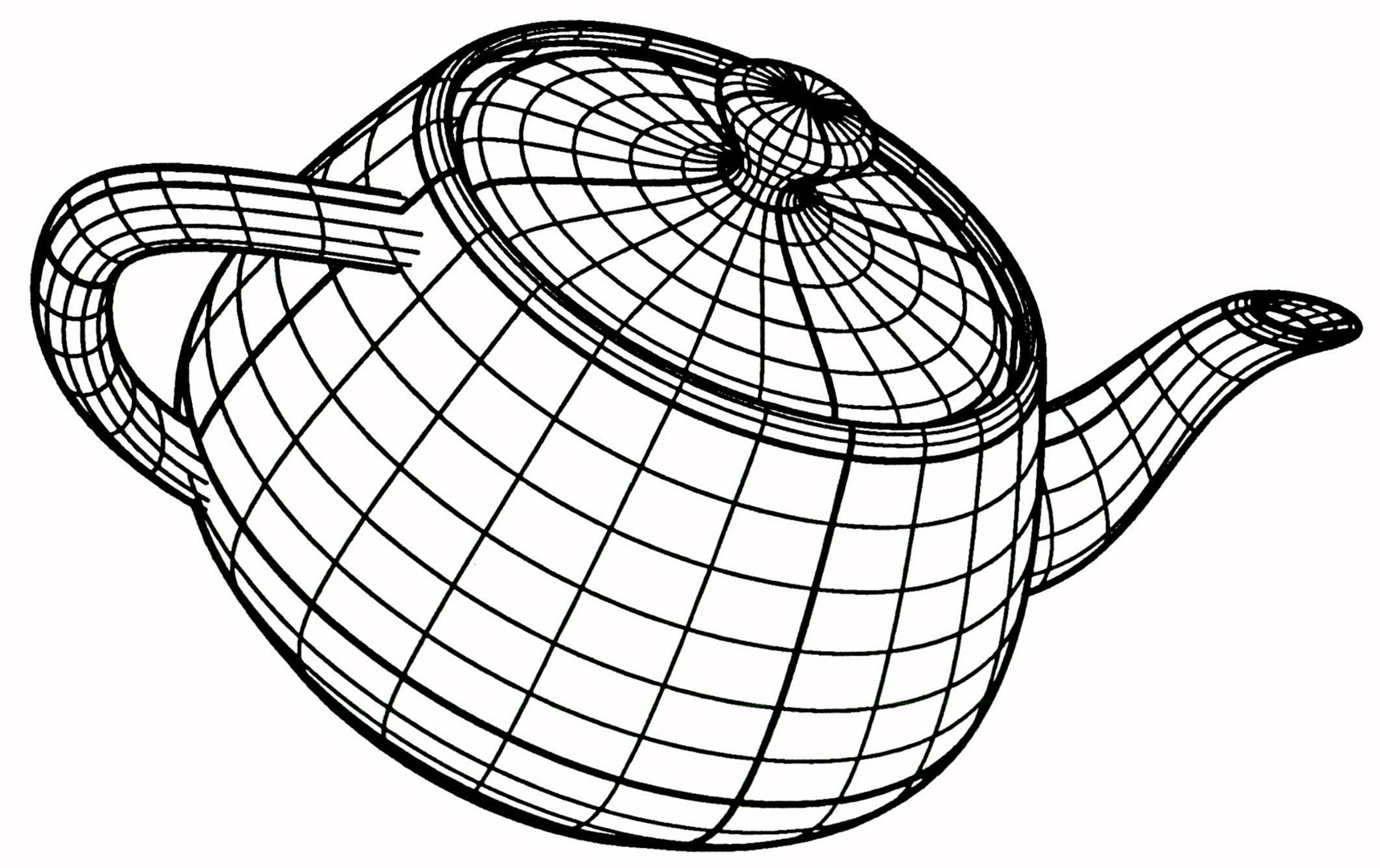
“Hidden curve removal for free form surfaces” by Elber and Cohen
Conference:
Type(s):
Title:
- Hidden curve removal for free form surfaces
Session/Category Title: Object Space Methods
Presenter(s)/Author(s):
Moderator(s):
Abstract:
This paper describes a hidden curve algorithm specifically designed for sculptured surfaces. A technique is described to extract the visible curves for a given scene without the need to approximate the surface by polygons. This algorithm produces higher quality results than polygon based algorithms, as most of the output set has an exact representation. Surface coherence is used to speed up the process. Although designed for sculptured surfaces, this algorithm is also suitable for polygonal data.
References:
1. A. Appel. The Notion of quantitative Invisibility and the Machine Rendering of Solids Proceedings A CM National Conference 1967.
2. J. Blirm. A scan line algorithm for displaying parametricaly defined surfaces. Computer Graphics 12.3. 1977.
3. B. Bruderlin, E. Cohen, and G. Elber. A Plane-Sweep Hidden-Surface Algorithm for Curved Surfaces. Technical report No. 90-006, Computer Science, University of Utah.
4. C. Sequin and P. Wensley. Visible Feature Return at Object Resolution. IEEE Computer Graphics and Application, May 1985, pp 27-50.
5. E. Cohen, T. Lyche, and R. Riesenfeld. Discrete B-splines and subdivision Techniques in Computer-Aided Geometric Design and Computer Graphics. Computer Graphics and Image Processing, 14, 87-111 (1980).
6. D. Griswold and M. Cohen. Automatic Illustration of 3D Geometric Models: Lines. Proceedings of the 1990 Symposium on Interactive 3D Graphics.
7. V. Fuson. Application of a Hidden Line Algorithm to Surface Visualization. MS thesis, Computer Science, University of Utah, 1984.
8. R. Galimberti and U. Montaaaari. An algoritlml for Hidden Line Elimination CACM 12, 4, 206, April 1969.
9. G. Hamlin and C. W. Gear. Raster-scan hidden surface algorithm techniques Computer Graphics, Vol 11, pp 206- 213, 1977.
10. C. Hornung. An Approach to a Calculation-Minimized Hidden Line Algorithm. Computer & Graphics, Vol 6, No 3, pp 121-126, 1982.
11. C. Hornung. A Method for Solving the Visibility Problem IEEE CG&A July 1984, pp. 26-33.
12. (3. Hornung, W. Lellek, P. Pehwald, and W. Strasser. An Area-Oriented Analytical Visiblity Method for Displaying Parametrically Defined Tensor-Product Surfaces. Computer Aided Geometric Design, 2 (1985) 197-205.
13. Foley and A. VanDam. Fundamental of interactive Computer Graphics.
14. G. Elber and E. Cohen. Hidden Curve Removal for Untrimmed and Trimmed NURB Surfaces. Technical report No. 89-019, Computer Science, University of Utah.
15. R. Guting. New Algorithm for Special Cases of the Hidden Line Elimination Problem. Computer Vision, Graphics, and Image Processing 40, 188-204 (1987).
16. I. Sutherland, R. Sproull, and R. Schumacker A Characterization of ten Hidden-Surface Algorithms. Computer Surveys, Vol. 6, No. 1, Max. 1974, pp. 1-55.
17. T. Kamada and S. Kawai. An Enhanced Treatment of Hidden Lines. ACM Transaction on Graphics, Vol 6, No. 4, October 1987, Pages 308-323.
18. J. Kripac. Classification of edges and its application in determining visibility. Computer Aided Design, Volume 17, Number 1, January/February 1985.
19. J. Lane and R. Riesenfeld. A Theoretical Development for the Computer Generation and Display of Piecewise Polynomial Surfaces. IEEE Transaction on pattern analysis and machine intelligence, vol. PAMI-2, No. 1, January 1980.
20. L. Li. Hidden-line algorithm for curved surfaces. Computer Aided Design, Volume 20, No. 8, October 1988, Pages 466- 470.
21. P. Loutrel. A Solution to the Hidden.line Problem for Computer Drawn Polyhedra IEEE Transactions on Computers, Vol. C-19, No. 3, 205-213, March 1970.
22. M. Mckerma. Worst-Case Optimal Hidden-Surface Removal. ACM Transaction on Graphics, Vol 6, No. 1, 2anuary 1987, Pages 19-28.
23. C. Montani and M. Re. Vector and Raster Hidden-Surface Removal Using Parallel Connected Stripes. IEEE Computer Graphics and Application, July 1987, pp 14-23.
24. O. Nurml. A Fast Line-Sweep Algorithm for Hidden Line Elimination. BIT 25 (1985}, pp 466-472.
25. J. Peterson. PItT – A High Quality Image Systhesis System for B-spline Sm~taces. MS thesis, Computer Science Dept., University of Utah, Dec. 1987′.
26. J. Ranldn. A Geometric Hidden-Line Processing Algorithm. Comput. & Graphics Vol. 11, No. 1, pp. 11-19. 1987′.
27. T. Sederberg and R. Meyers. Loop Detection in Surface P~tch Intersections. Computer Aided Geometric Design 5, pp 161-17’1, 1988.
28. T. Sederberg and S. Parry. Comparison of Three Curve Intersection Algorithms. Computer Aided Design, Volume 18, Number 1, January/February 1986.
29. M. Sweeney. Ray Tracing Free-Form B-Spline Surfaces. IEEE Computer Graphics and Application, Februaury 1986, pp 41-49.