“Handle-aware isolines for scalable shape editing” by Kin-Chung Au, Fu, Tai and Cohen-Or

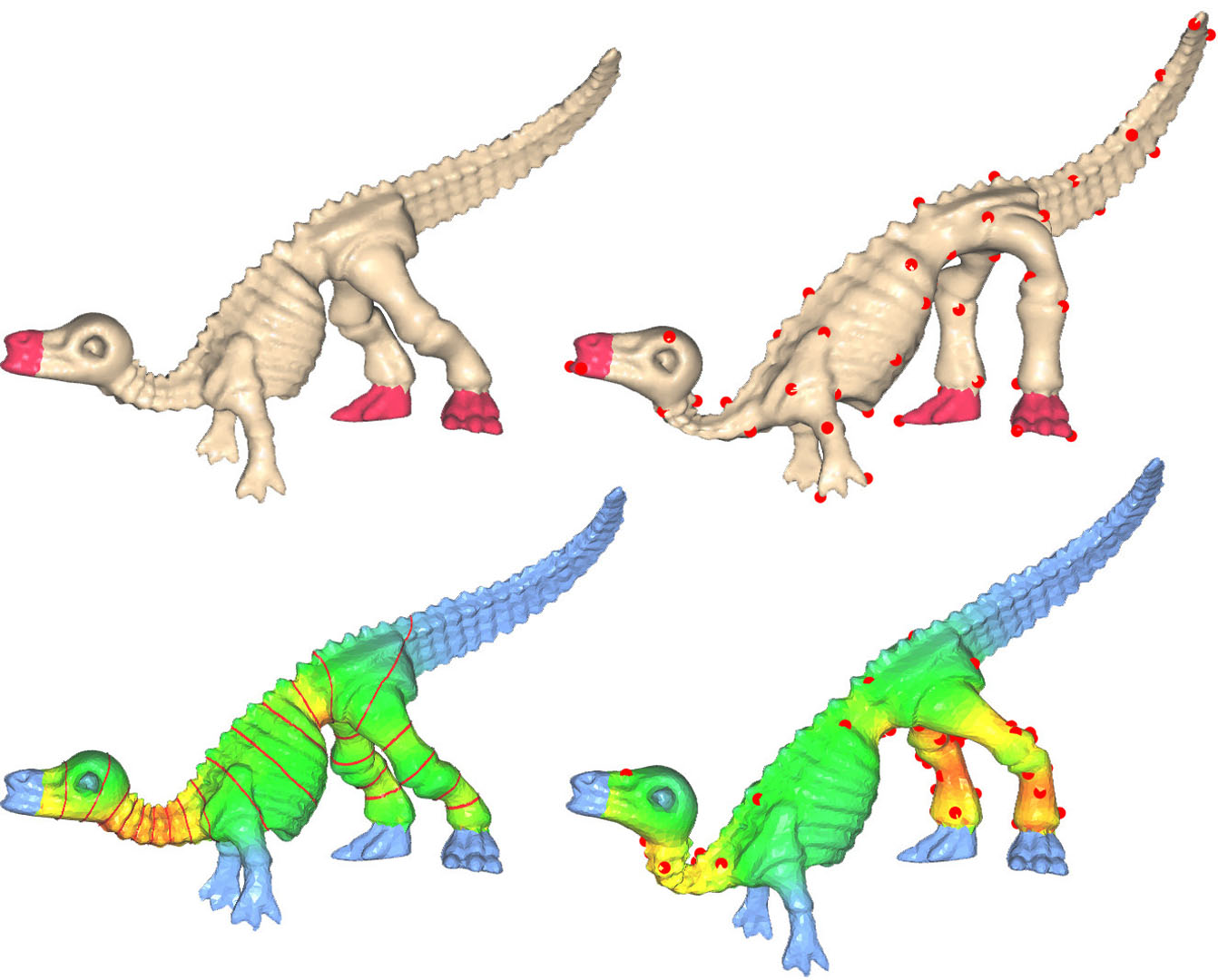
Handle-based mesh deformation is essentially a nonlinear problem. To allow scalability, the original deformation problem can be approximately represented by a compact set of control variables. We show the direct relation between the locations of handles on the mesh and the local rigidity under deformation, and introduce the notion of handle-aware rigidity. Then, we present a reduced model whose control variables are intelligently distributed across the surface, respecting the rigidity information and the geometry. Specifically, for each handle, the control variables are the transformations of the isolines of a harmonic scalar field representing the deformation propagation from that handle. The isolines constitute a virtual skeletal structure similar to the bones in skinning deformation, thus correctly capturing the low-frequency shape deformation. To interpolate the transformations from the isolines to the original mesh, we design a method which is local, linear and geometry-dependent. This novel interpolation scheme and the transformation-based reduced domain allow each iteration of the nonlinear solver to be fully computed over the reduced domain. This makes the per-iteration cost dependent on only the number of isolines and enables compelling deformation of highly detailed shapes at interactive rates. In addition, we show how the handle-driven isolines provide an efficient means for deformation transfer without full shape correspondence.

1. Aksoylu, B., Khodakovsky, A., and Schröder, P. 2005. Multilevel solvers for unstructured surface meshes. SIAM Journal on Scientific Computing 26, 4, 1146–1165. Google ScholarDigital Library
2. Au, O. K.-C., Tai, C.-L., Fu, H., and Liu, L. 2005. Mesh editing with curvature flow laplacian operator. Tech. rep., Hong Kong University of Science Technology, Computer Science Technical Report, HKUST-CS05-10.Google Scholar
3. Au, O. K.-C., Tai, C.-L., Liu, L., and Fu, H. 2006. Dual Laplacian editing for meshes. IEEE Transaction on Visualization and Computer Graphics 12, 3, 386–395. Google ScholarDigital Library
4. Botsch, M., and Kobbelt, L. 2004. An intuitive framework for real-time freeform modeling. ACM Trans. Graph. 23, 3, 630–634. Google ScholarDigital Library
5. Botsch, M., and Kobbelt, L. 2005. Real-time shape editing using radial basis functions. In Eurographics, 611–621.Google Scholar
6. Botsch, M., Pauly, M., Gross, M., and Kobbelt, L. 2006. PriMo: coupled prisms for intuitive surface modeling. In Symposium on Geometry Processing, 11–20. Google ScholarDigital Library
7. Der, K. G., Sumner, R. W., and Popović, J. 2006. Inverse kinematics for reduced deformable models. ACM Trans. Graph. 25, 3, 1174–1179. Google ScholarDigital Library
8. Fu, H., Au, O. K.-C., and Tai, C.-L. 2007. Effective derivation of similarity transformations for implicit Laplacian mesh editing. Computer Graphics Forum 26, 1, 34–45.Google ScholarCross Ref
9. Garland, M., and Heckbert, P. S. 1997. Surface simplification using quadric error metrics. In SIGGRAPH ’97, 209–216. Google ScholarDigital Library
10. Huang, J., Shi, X., Liu, X., Zhou, K., Wei, L.-Y., Teng, S.-H., Bao, H., Guo, B., and Shum, H.-Y. 2006. Subspace gradient domain mesh deformation. ACM Trans. Graph. 25, 3, 1126–1134. Google ScholarDigital Library
11. Igarashi, T., Moscovich, T., and Hughes, J. F. 2005. Asrigid-as-possible shape manipulation. ACM Trans. Graph. 24, 3, 1134–1141. Google ScholarDigital Library
12. James, D. L., and Twigg, C. D. 2005. Skinning mesh animations. ACM Trans. Graph. 24, 3, 399–407. Google ScholarDigital Library
13. Ju, T., Schaefer, S., and Warren, J. 2005. Mean value coordinates for closed triangular meshes. ACM Trans. Graph. 24, 3, 561–566. Google ScholarDigital Library
14. Kobbelt, L., Campagna, S., Vorsatz, J., and Seidel, H.-P. 1998. Interactive multi-resolution modeling on arbitrary meshes. In Proceedings of ACM SIGGRAPH 98, 105–114. Google ScholarDigital Library
15. Lewis, J. P., Cordner, M., and Fong, N. 2000. Pose space deformation: a unified approach to shape interpolation and skeleton-driven deformation. In Proceedings of ACM SIGGRAPH 2000, 165–172. Google ScholarDigital Library
16. Lindholm, E., Kligard, M. J., and Moreton, H. 2001. A user-programmable vertex engine. In SIGGRAPH 2001, 149–158. Google ScholarDigital Library
17. Lipman, Y., Sorkine, O., Cohen-Or, D., Levin, D., Rössl, C., and Seidel, H.-P. 2004. Differential coordinates for interactive mesh editing. In Proceedings of Shape Modeling International, IEEE Computer Society Press, 181–190. Google ScholarDigital Library
18. Lipman, Y., Sorkine, O., Levin, D., and Cohen-Or, D. 2005. Linear rotation-invariant coordinates for meshes. ACM Trans. Graph. 24, 479–487. Google ScholarDigital Library
19. Lipman, Y., Cohen-Or, D., Gal, R., and Levin, D. 2007. Volume and shape preservation via moving frame manipulation. ACM Trans. Graph. 26, 1, 5. Google ScholarDigital Library
20. Mohr, A., and Gleicher, M. 2003. Building efficient, accurate character skins from examples. ACM Trans. Graph. 22, 3, 562–568. Google ScholarDigital Library
21. Sederberg, T. W., and Parry, S. R. 1986. Free-form deformation of solid geometric models. In Computer Graphics (Proceedings of ACM SIGGRAPH 86), 151–160. Google ScholarDigital Library
22. Shi, L., Yu, Y., Bell, N., and Feng, W.-W. 2006. A fast multigrid algorithm for mesh deformation. ACM Trans. Graph. 25, 3, 1108–1117. Google ScholarDigital Library
23. Sorkine, O., Lipman, Y., Cohen-Or, D., Alexa, M., Rössl, C., and Seidel, H.-P. 2004. Laplacian surface editing. In Symposium on Geometry Processing, 179–188. Google ScholarDigital Library
24. Sorkine, O. 2006. Differential representations for mesh processing. Computer Graphics Forum 25, 4, 789–807.Google ScholarCross Ref
25. Sumner, R. W., and Popović, J. 2004. Deformation transfer for triangle meshes. ACM Trans. Graph. 23, 3, 399–405. Google ScholarDigital Library
26. Toledo, S., 2003. TAUCS: a library of sparse linear solvers, version 2.2. Tel-Aviv University, Available online at http://www.tau.ac.il/stoledo/taucs/.Google Scholar
27. Weng, Y., Xu, W., Wu, Y., Zhou, K., and Guo, B. 2006. 2D shape deformation using nonlinear least squares optimization. In The Visual Computer (Pacific Graphics 2006), 653–660. Google ScholarDigital Library
28. Yu, Y., Zhou, K., Xu, D., Shi, X., Bao, H., Guo, B., and Shum, H.-Y. 2004. Mesh editing with Poisson-based gradient field manipulation. ACM Trans. Graph. 23, 3, 644–651. Google ScholarDigital Library
29. Zayer, R., Rössl, C., Karni, Z., and Seidel, H.-P. 2005. Harmonic guidance for surface deformation. Computer Graphics Forum 24, 3, 601–609.Google ScholarCross Ref
30. Zhou, K., Huang, J., Snyder, J., Liu, X., Bao, H., Guo, B., and Shum, H.-Y. 2005. Large mesh deformation using the volumetric graph Laplacian. ACM Trans. Graph. 24, 3, 496–503. Google ScholarDigital Library