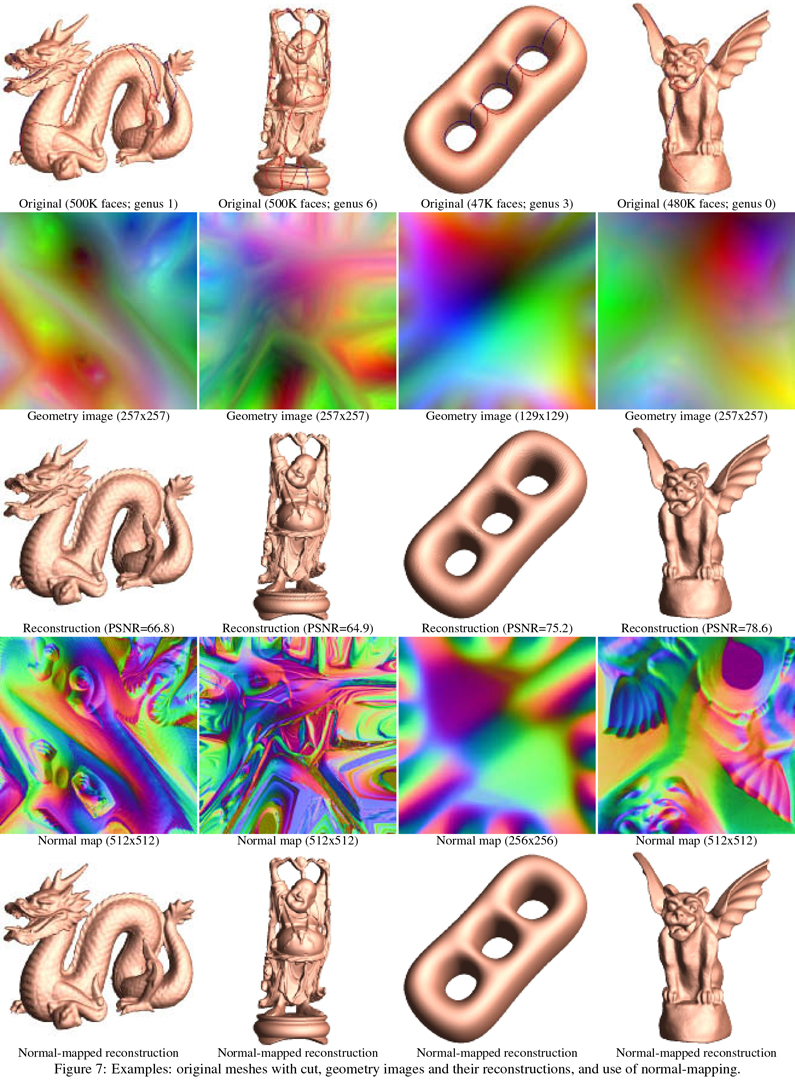
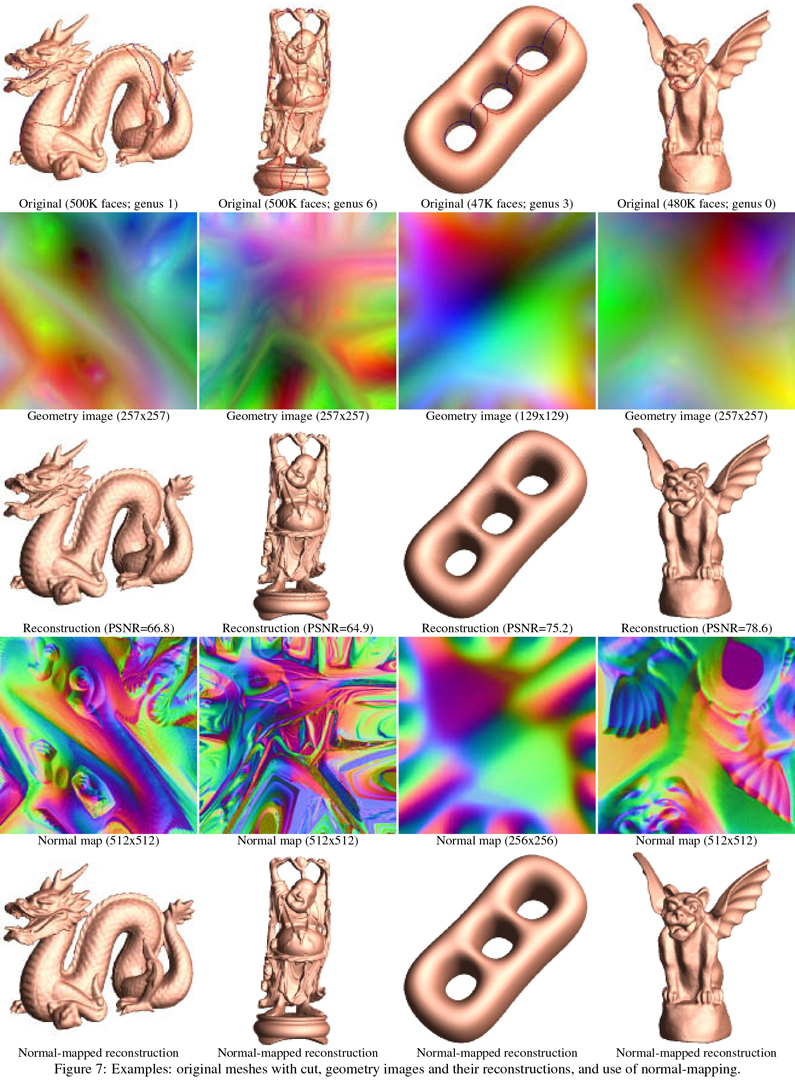
“Geometry images” by Gu, Gortler and Hoppe

Surface geometry is often modeled with irregular triangle meshes. The process of remeshing refers to approximating such geometry using a mesh with (semi)-regular connectivity, which has advantages for many graphics applications. However, current techniques for remeshing arbitrary surfaces create only semi-regular meshes. The original mesh is typically decomposed into a set of disk-like charts, onto which the geometry is parametrized and sampled. In this paper, we propose to remesh an arbitrary surface onto a completely regular structure we call a geometry image. It captures geometry as a simple 2D array of quantized points. Surface signals like normals and colors are stored in similar 2D arrays using the same implicit surface parametrization — texture coordinates are absent. To create a geometry image, we cut an arbitrary mesh along a network of edge paths, and parametrize the resulting single chart onto a square. Geometry images can be encoded using traditional image compression algorithms, such as wavelet-based coders.

1. DAVIS, G. Wavelet Image Compression Construction Kit. http://www.geoffdavis.net/dartmouth/wavelet/wavelet.html.Google Scholar
2. DEY, T. K., AND SCHIPPER, H. A new technique to compute polygonal schema for 2-manifolds with application to null-homotopy detection. Discrete and Computational Geometry 14 (1995), 93-110.Google Scholar
3. ECK, M., DEROSE, T., DUCHAMP, T., HOPPE, H., LOUNSBERY, M., AND STUETZLE, W. Multiresolution Analysis of Arbitrary Meshes. In SIGGRAPH 95, pp. 173-182. Google Scholar
4. ERICKSON, J., AND HAR-PELED, S. Cutting a surface into a disk. ACM SoCG 2002. Google Scholar
5. FERGUSON, H., ROCKWOOD, A., AND COX, J. Topological design of sculptured surfaces. In SIGGRAPH 92, pp. 149-156. Google Scholar
6. FLOATER, M. Parametrization and smooth approximation of surface triangulations. CAGD 14, 3 (1997), 231-250. Google Scholar
7. GUSKOV, I., VIDIMCE, K., SWELDENS, W., AND SCHRÖDER, P. Normal Meshes. In SIGGRAPH 2000, pp. 95-102. Google Scholar
8. HAKER, S., ANGENENT, S., TANNENBAUM, A., KIKINIS, R., SAPIRO, G., AND HALLE, M. Conformal Surface Parameterization for Texture Mapping. IEEE TVCG 6, 2 (2000), 181-189. Google Scholar
9. HOPPE, H. Progressive Meshes. In SIGGRAPH 96, pp. 99-108. Google Scholar
10. KHODAKOVSKY, A., SCHRÖDER, P., AND SWELDENS, W. Progressive Geometry Compression. In SIGGRAPH 2000, pp. 271-278. Google Scholar
11. LAZARUS, F., POCCHIOLA, M., VEGTER, G., AND VERROUST, A. Computing a Canonical Polygonal Schema of an Orientable Triangulated Surface. In ACM SoCG 2001, pp. 80-89. Google Scholar
12. LEE, A., MORETON, H., AND HOPPE, H. Displaced Subdivision Surfaces. In SIGGRAPH 2000, pp. 85-94. Google Scholar
13. LEE, A., SWELDENS, W., SCHRÖDER, P., COWSAR, L., AND DOBKIN, D. MAPS: Multiresolution Adaptive Parameterization of Surfaces. In SIGGRAPH 98, pp. 95-104. Google Scholar
14. LOUNSBERY, M., DEROSE, T., AND WARREN, J. Multiresolution Analysis for Surfaces of Arbitrary Topological Type. ACM TOG 16, 1 (January 1997), 34-73. Google Scholar
15. MUNKRES, J. Topology. Prentice Hall, 2000.Google Scholar
16. PIPONI, D., AND BORSHUKOV, G. D. Seamless Texture Mapping of Subdivision Surfaces by Model Pelting and Texture Blending. In SIGGRAPH 2000, pp. 471-478. Google Scholar
17. SANDER, P., GORTLER, S., SNYDER, J., AND HOPPE, H. Signal-Specialized Parametrization. Microsoft Research MSR-TR-2002-27 (January 2002). Google Scholar
18. SANDER, P., SNYDER, J., GORTLER, S., AND HOPPE, H. Texture Mapping Progressive Meshes. In SIGGRAPH 2001, pp. 409-416. Google Scholar
19. SHEFFER, A. Spanning Tree Seams for Reducing Parameterization Distortion of Triangulated Surfaces. Shape Modelling International (2002). Google Scholar
20. TAUBIN, G., AND ROSSIGNAC, J. Geometric compression through topological surgery. ACM TOG 17, 2 (1998), 84-115. Google Scholar
21. VEGTER, G., AND YAP, C. K. Computational complexity of combinatorial surfaces. In ACM SoCG 1990, pp. 102-111. Google Scholar
22. VORSATZ, J., RÖSSL, C., KOBBELT, L., AND SEIDEL, H.-P. Feature Sensitive Remeshing. Computer Graphics Forum 20, 3 (2001), 393-401.Google Scholar
23. WOOD, Z., HOPPE, H., DESBRUN, M., AND SCHRÖDER, P. Isosurface topology simplification. Microsoft Research MSR-TR-2002-28 (January 2002).Google Scholar
24. ZORIN, D., SCHRÖDER, P., AND SWELDENS, W. Interactive multiresolution mesh editing. In SIGGRAPH 97, pp. 259-268. Google Scholar