“Generic objective vortices for flow visualization” by Günther, Gross and Theisel
Conference:
Type(s):
Title:
- Generic objective vortices for flow visualization
Session/Category Title: Fluids III
Presenter(s)/Author(s):
Moderator(s):
Abstract:
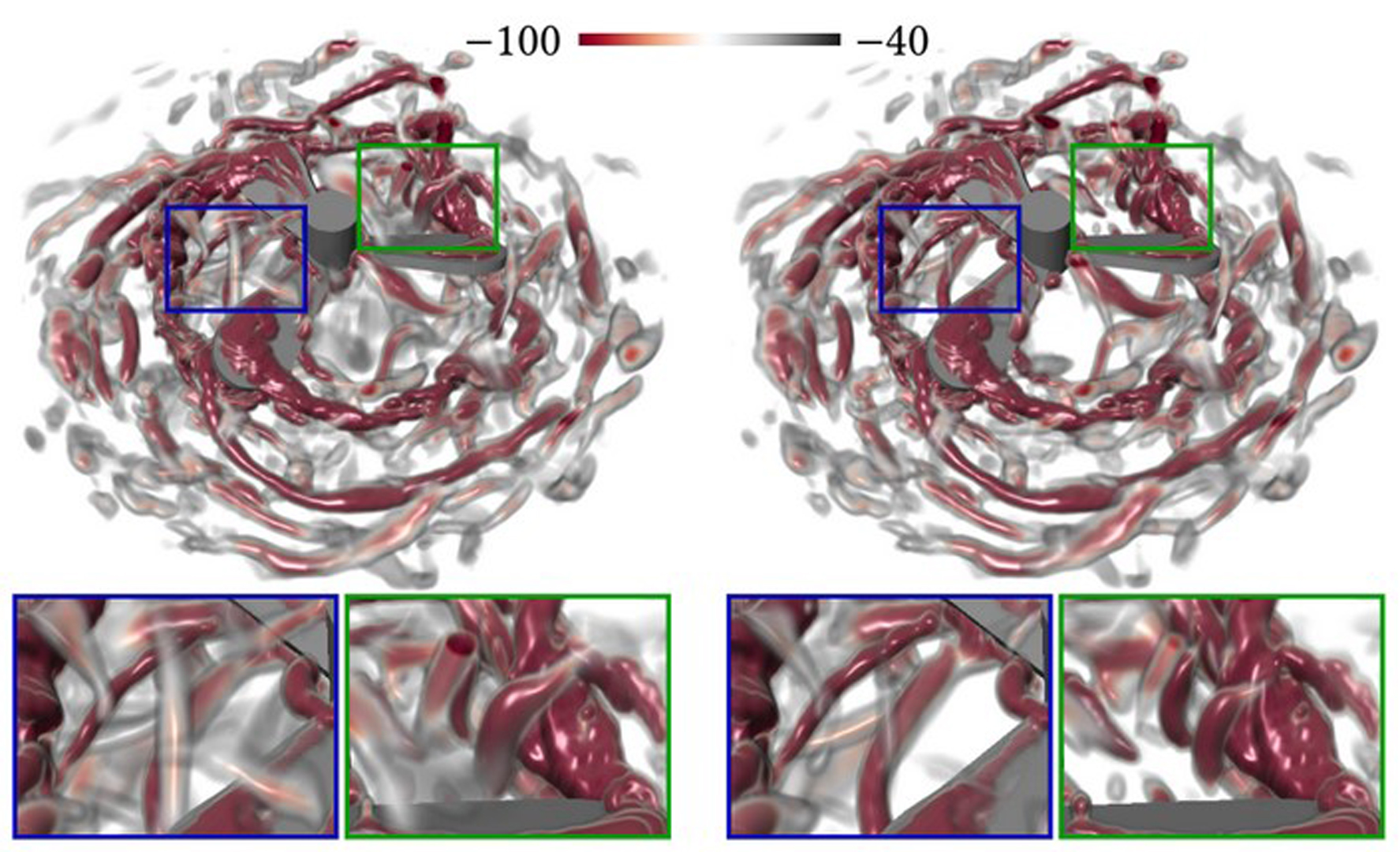
In flow visualization, vortex extraction is a long-standing and unsolved problem. For decades, scientists developed numerous definitions that characterize vortex regions and their corelines in different ways, but none emerged as ultimate solution. One reason is that almost all techniques have a fundamental weakness: they are not invariant under changes of the reference frame, i.e., they are not objective. This has two severe implications: First, the result depends on the movement of the observer, and second, they cannot track vortices that are moving on arbitrary paths, which limits their reliability and usefulness in practice. Objective measures are rare, but recently gained more attention in the literature. Instead of only introducing a new objective measure, we show in this paper how all existing measures that are based on velocity and its derivatives can be made objective. We achieve this by observing the vector field in optimal local reference frames, in which the temporal derivative of the flow vanishes, i.e., reference frames in which the flow appears steady. The central contribution of our paper is to show that these optimal local reference frames can be found by a simple and elegant linear optimization. We prove that in the optimal frame, all local vortex extraction methods that are based on velocity and its derivatives become objective. We demonstrate our approach with objective counterparts to λ2, vorticity and Sujudi-Haimes.
References:
1. Gianni Astarita. 1979. Objective and generally applicable criteria for flow classification. Journal of Non-Newtonian Fluid Mechanics 6, 1 (1979), 69–76. Google ScholarCross Ref
2. Dirk Bauer and Ronald Peikert. 2002. Vortex Tracking in Scale-space. In Proc. Symposium on Data Visualisation. 233–240.Google Scholar
3. H. Bhatia, G. Norgard, V. Pascucci, and Peer-Timo Bremer. 2013. The Helmholtz-Hodge Decomposition-A Survey. IEEE Transactions on Visualization and Computer Graphics 19, 8 (2013), 1386–1404.Google ScholarDigital Library
4. Harsh Bhatia, Valerio Pascucci, Robert M. Kirby, and Peer-Timo Bremer. 2014. Extracting Features from Time-Dependent Vector Fields Using Internal Reference Frames. Computer Graphics Forum (Proc. EuroVis) 33, 3 (2014), 21–30.Google ScholarCross Ref
5. R. Bujack, M. Hlawitschka, and K. I. Joy. 2016. Topology-inspired Galilean invariant vector field analysis. In IEEE Pacific Visualization Symposium. 72–79. Google ScholarCross Ref
6. S. Camarri, M.-V. Salvetti, M. Buffoni, and A. Iollo. 2005. Simulation of the three-dimensional flow around a square cylinder between parallel walls at moderate Reynolds numbers. In XVII Congresso di Meccanica Teorica ed Applicata.Google Scholar
7. R Drouot and M Lucius. 1976. Approximation du second ordre de la loi de comportement des fluides simples. Lois classiques déduites de lâĂŹintroduction dâĂŹun nouveau tenseur objectif. Archiwum Mechaniki Stosowanej 28, 2 (1976), 189–198.Google Scholar
8. T. Günther, Maik Schulze, and H. Theisel. 2016. Rotation Invariant Vortices for Flow Visualization. IEEE Transactions on Visualization and Computer Graphics (Proc. IEEE SciVis 2015) 22, 1 (2016), 817–826.Google Scholar
9. T. Günther and H. Theisel. 2014. Vortex Cores of Inertial Particles. IEEE Transactions on Visualization and Computer Graphics (Proc. IEEE SciVis) 20, 12 (2014), 2535–2544.Google Scholar
10. G. Haller. 2005. An objective definition of a vortex. Journal of Fluid Mechanics 525 (2005), 1–26. Google ScholarCross Ref
11. George Haller. 2015. Lagrangian coherent structures. Annual Review of Fluid Mechanics 47 (2015), 137–162. Google ScholarCross Ref
12. George Haller, Alireza Hadjighasem, Mohammad Farazmand, and Florian Huhn. 2016. Defining coherent vortices objectively from the vorticity. Journal of Fluid Mechanics 795 (2016), 136–173. Google ScholarCross Ref
13. J. C. R. Hunt. 1987. Vorticity and vortex dynamics in complex turbulent flows. Transactions on Canadian Society for Mechanical Engineering (Proc. CANCAM) 11, 1 (1987), 21–35.Google Scholar
14. Jinhee Jeong and Fazle Hussain. 1995. On the identification of a vortex. Journal of Fluid Mechanics 285 (1995), 69–94. Google ScholarCross Ref
15. Jens Kasten, Ingrid Hotz, Bernd R. Noack, and Hans-Christian Hege. 2011a. On the Extraction of Long-living Features in Unsteady Fluid Flows. In Topological Methods in Data Analysis and Visualization. 115 — 126. Google ScholarCross Ref
16. Jens Kasten, Jan Reininghaus, Ingrid Hotz, and Hans-Christian Hege. 2011b. Two-Dimensional Time-Dependent Vortex Regions Based on the Acceleration Magnitude. IEEE Transactions on Visualization and Computer Graphics (Proc. IEEE SciVis) 17, 12 (2011), 2080–2087.Google Scholar
17. J. Kasten, J. Reininghaus, Hotz I., H.-C. Hege, B.R. Noack, G. Daviller, and M. Morzynski. 2016. Acceleration feature points of unsteady shear flows. Archives of Mechanics 68, 1 (2016), to appear.Google Scholar
18. RobertS. Laramee, Helwig Hauser, Lingxiao Zhao, and FritsH. Post. 2007. Topology-Based Flow Visualization, The State of the Art. In Topology-based Methods in Visualization. Springer Berlin Heidelberg, 1–19. Google ScholarCross Ref
19. Hans J Lugt. 1979. The dilemma of defining a vortex. In Recent developments in theoretical and experimental fluid mechanics. Springer, 309–321.Google Scholar
20. R. S. Martins, A. S. Pereira, G. Mompean, L. Thais, and R. L. Thompson. 2016. An objective perspective for classic flow classification criteria. Comptes Rendus Mecanique 344 (Jan. 2016), 52–59. arXiv:physics.flu-dyn/1506.03384 Google ScholarCross Ref
21. Akira Okubo. 1970. Horizontal dispersion of floatable particles in the vicinity of velocity singularities such as convergences. Deep Sea Research and Oceanographic Abstracts 17, 3 (1970), 445–454. Google ScholarCross Ref
22. Ronald Peikert and Martin Roth. 1999. The “Parallel Vectors” Operator – A Vector Field Visualization Primitive. In Proc. IEEE Visualization. 263–270. Google ScholarCross Ref
23. A. E. Perry and M. S. Chong. 1994. Topology of Flow Patterns in Vortex Motions and Turbulence. Applied Scientific Research 53, 3 (1994), 357–374. Google ScholarCross Ref
24. Stèphane Popinet. 2004. Free computational fluid dynamics. Cluster World 2 6 (2004).Google Scholar
25. Frits H. Post, Benjamin Vrolijk, Helwig Hauser, Robert S. Laramee, and Helmut Doleisch. 2003. The State of the Art in Flow Visualisation: Feature Extraction and Tracking. Computer Graphics Forum 22, 4 (2003), 775–792. Google ScholarCross Ref
26. Martin Roth and Ronald Peikert. 1998. A higher-order method for finding vortex core lines. In Proc. IEEE Visualization. 143–150. Google ScholarCross Ref
27. J. Sahner, T. Weinkauf, and H.-C. Hege. 2005. Galilean Invariant Extraction and Iconic Representation of Vortex Core Lines. In Proc. EuroVis). 151–160.Google Scholar
28. J. Sahner, T. Weinkauf, N. Teuber, and H.-C. Hege. 2007. Vortex and Strain Skeletons in Eulerian and Lagrangian Frames. IEEE Trans. Vis. and Computer Graphics 13, 5 (2007), 980–990. Google ScholarDigital Library
29. T. Schafhitzel, J. Vollrath, J. Gois, D. Weiskopf, A. Castelo, and T. Ertl. 2008. Topology-Preserving lambda2-based Vortex Core Line Detection for Flow Visualization. Computer Graphics Forum (Proc. EuroVis) 27, 3 (2008), 1023–1030.Google ScholarDigital Library
30. Mattia Serra and George Haller. 2016a. Forecasting Long-Lived Lagrangian Vortices from their Objective Eulerian Footprints. J. Fluid Mech. (2016), to appear.Google Scholar
31. Mattia Serra and George Haller. 2016b. Objective Eulerian coherent structures. Chaos: An Interdisciplinary Journal of Nonlinear Science 26, 5 (2016), 053110.Google ScholarCross Ref
32. D. Sujudi and R. Haimes. 1995. Identification of Swirling Flow in 3D Vector Fields. Technical Report. Departement of Aeronautics and Astronautics, MIT. AIAA Paper 95–1715.Google Scholar
33. Michael Tabor and I Klapper. 1994. Stretching and alignment in chaotic and turbulent flows. Chaos, Solitons & Fractals 4, 6 (1994), 1031–1055. Google ScholarCross Ref
34. H. Theisel, J. Sahner, T. Weinkauf, H.-C. Hege, and H.-P. Seidel. 2005. Extraction of parallel vector surfaces in 3D time-dependent fields and application to vortex core line tracking. In Proc. IEEE Visualization. 631–638. Google ScholarCross Ref
35. H. Theisel and H.-P. Seidel. 2003. Feature Flow Fields. In Proc. Symposium on Data Visualisation. 141–148.Google Scholar
36. Roney L Thompson. 2008. Some perspectives on the dynamic history of a material element. International Journal of Engineering Science 46, 3 (2008), 224–249. Google ScholarCross Ref
37. Yiying Tong, Santiago Lombeyda, Anil N. Hirani, and Mathieu Desbrun. 2003. Discrete Multiscale Vector Field Decomposition. ACM Trans. Graph. (Proc. SIGGRAPH) 22, 3 (2003), 445–452.Google ScholarDigital Library
38. Clifford Truesdell and Walter Noll. 1965. The nonlinear field theories of mechanics. Handbuch der Physik, Band III/3, e by Flugge, S., (ed.), Springer-Verlag, Berlin.Google Scholar
39. T. Weinkauf, J. Sahner, H. Theisel, and H.-C. Hege. 2007. Cores of Swirling Particle Motion in Unsteady Flows. IEEE Transactions on Visualization and Computer Graphics (Proc. Visualization) 13, 6 (2007), 1759–1766.Google ScholarDigital Library
40. John Weiss. 1991. The dynamics of enstrophy transfer in two-dimensional hydrodynamics. Physica D: Nonlinear Phenomena 48, 2–3 (1991), 273–294.Google ScholarDigital Library