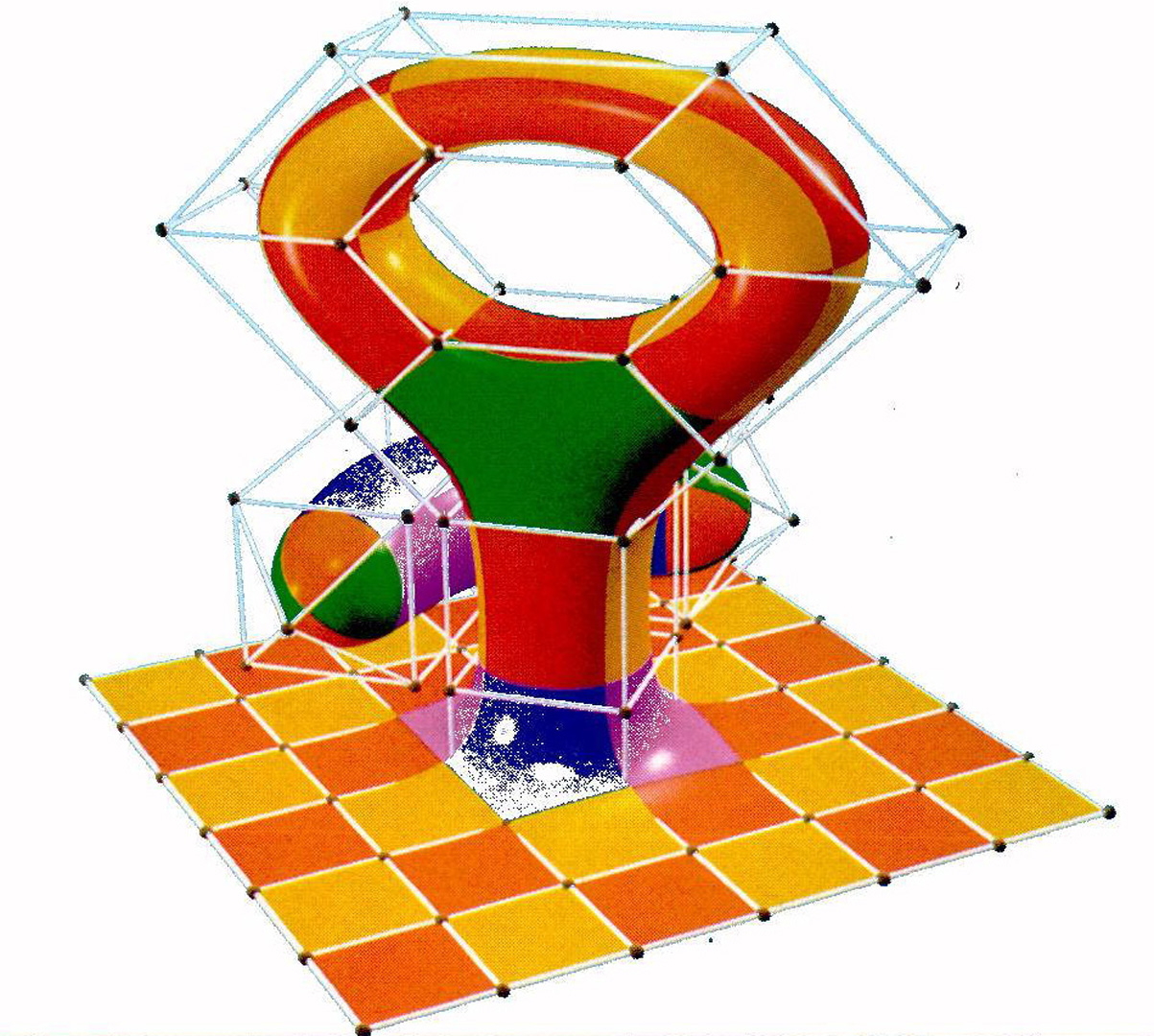
“Generalized B-spline surfaces of arbitrary topology” by Loop and DeRose
Conference:
Type(s):
Title:
- Generalized B-spline surfaces of arbitrary topology
Session/Category Title: Surfaces and Volumes
Presenter(s)/Author(s):
Moderator(s):
Abstract:
B-spline surfaces, although widely used, are incapable of describing surfaces of arbitrary topology. It is not possible to model a general closed surface or a surface with handles as a single non-degenerate B-spline. In practice such surfaces are often needed. In this paper, we present generalizations of biquadratic and bicubic B-spline surfaces that are capable of capturing surfaces of arbitrary topology (although restrictions are placed on the connectivity of the control mesh). These results are obtained by relaxing the sufficient but not necessary smoothness constraints imposed by B-splines and through the use of an n-sided generalization of Bézier surfaces called S-patches.
References:
1. Boehm, Wolfgang. Cubic B-spline curves and surfaces in computer aided geometric design. Computing, 19:29-34, 1977.
2. Boehm, Wolfgang. Generating the B~zier points of B- splines. Computer Aided Design, 13(6):365-366, 1981.
3. Boehm, Wolfgang. Visual continuity. Computer Aided Design, 20(6):307-311, 1988.
4. CatmulI, Edwin and James Clark. Recursively generated B-spline surfaces on arbitrary topological meshes. Computer Aided Design, 10(6):350-355, 1978.
5. Charrot, Peter and John Gregory. A pentagonal surface patch for computer aided geometric design. Compnter Aided Geometric Design, 1(1):87-94, 1984.
6. Chiyokura, Hiroaki and Fumihiko Kimura. Design of solids with free-form surfaces. Computer Graphics, 17(3):289-298, 1983.
7. de Boor, Carl. B-form basics. In G. Farin, editor, Geometric Modeling: Algorithms and New 7kends, pages 131-148. SIAM, 1987.
8. DeRose, Tony. Geometric Continuity: A Parametrization Independent Measure of Continuity for Computer Aided Geometric Design. PhD thesis, Berkeley, 1985. also available as Technical report UCB/CSD 86/255.
9. Dog, Daniel and Malcolm Sabin. B~h~iou~ of r~~i~ division surfaces near extraordinary points. Computer Aided Design, 10(6):356-360, 1978.
10. Gregory, John and JSrg Hahn. A C9 polygonal surface patch. Computer Aided Geometric Design, 6(1):69-75, 1989.
11. Gregory, John. N-sided surface patches. In J. Gregory, editor, The Mathematics of Surfaces, pages 217- 232. Clarendon Press, 1986.
12. Guibas, Leo and Jorge Stolfi. Primitives for the manipulation of general subdivisions ~nd the computation of voronoi diagrams. A CM Transactions on Graphics, 4(2):74-123, 1985.
13. Hahn, JSrg Filiirtg polygonal holes with rectangular patches. In W. Strasser and H.P. Seidel, editors, Geometric Modeling: Algorithms and New Trends, pages 81-91. Spring-Verlag, 1989.
14. Herron, Gary. Triangular and Multisided Patck Schemes. PhD thesis, U. of Utah, 1979.
15. Herron, Gary. Smooth closed surfaces with discrete triangular interpolants. Computer Aided Design, 2(4):297- 306, 1985.
16. Herron, Gary. Techniques for visual continuity. In G. Farin, editor, Geometric Modeling, pages 163-174. SIAM, 1987.
17. Hosaka, Mamoru and Fumihiko Kimura. Non-four-sided patch expressions with control points. Computer Aided Geometric Design, 1(1):75-86, 1984.
18. Loop, Charles and Tony DeRose. A multisided generalization of B~zier surfaces. A CM Transactions on Graphics, 8(3):204-234, 1989.
19. Sabin, Malcolm. Non-rectangular surface patches suitable for inclusion in a B-spline surface. In P. ten Hagen, editor, Proceedings of Eurographics ’83, pages 57-69. North- Holland, 1983.
20. Sablonniere, Paul. Sptine and B6zier polygons associated with a polynomial spline curve. Computer Aided Design, 10(4):257-261, 1978.
21. van Wijk, Jarke. Bicubie patches for approximating nonrectangular control-point meshes. Computer Aided Geometric Design, 3(1):1-13, 1986.
22. Varady, Tamas. Survey and new results in n-sided patch generation. In R. Martin, editor, -The Mathematics of Surfaces II~ pages 203-236. Oxford University Press, 1987.