“General Primitives for Smooth Coloring of Vector Graphics” by Batra, Phogat and Kavidayal
Conference:
Type(s):
Entry Number: 35
Title:
- General Primitives for Smooth Coloring of Vector Graphics
Presenter(s)/Author(s):
Abstract:
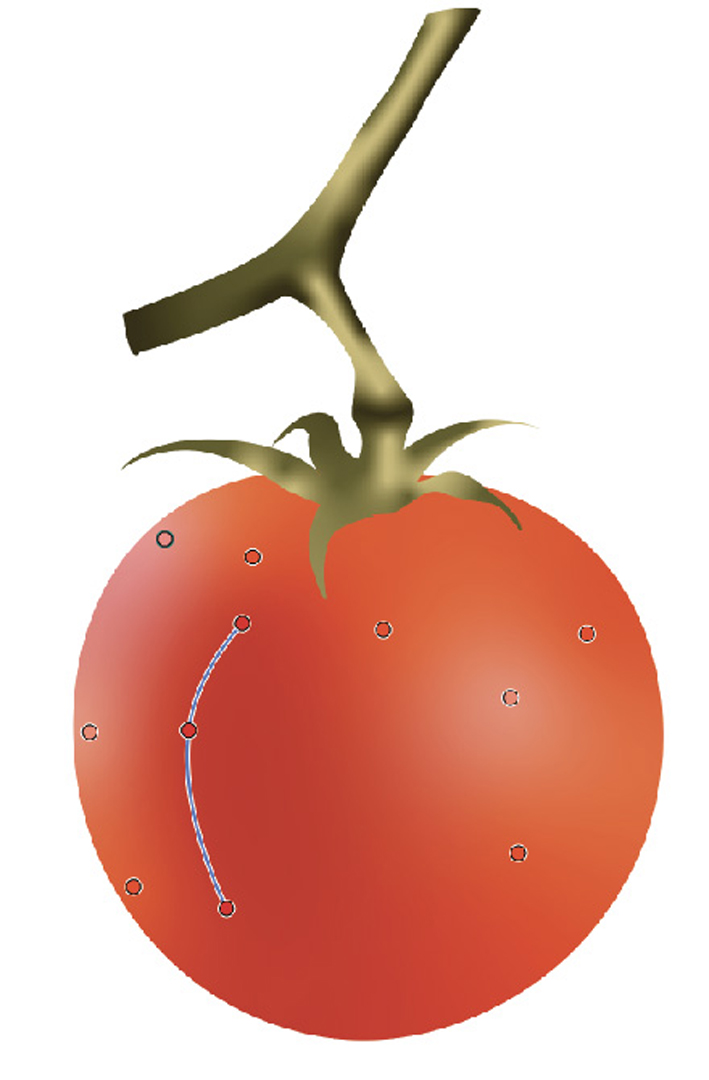
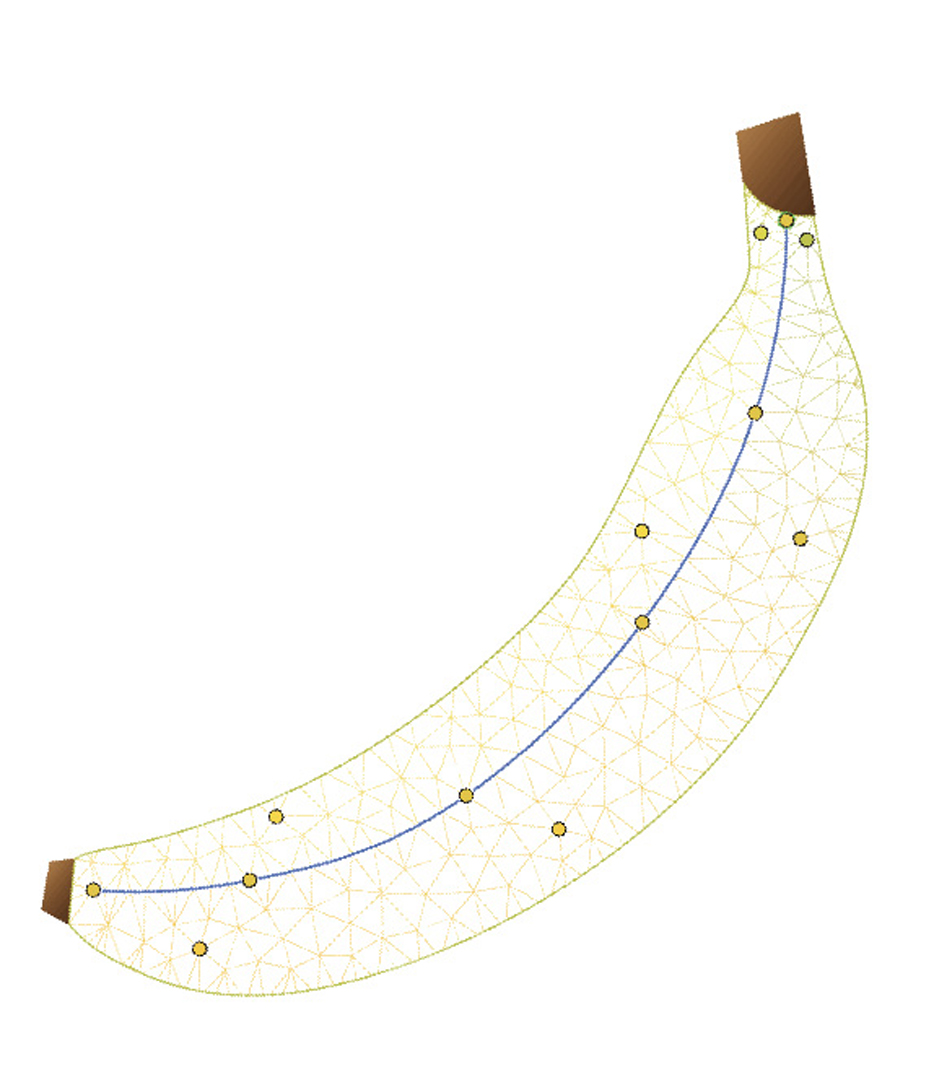
We propose a novel and intuitive method for coloring vector graphics which is easy to use and creates richly colored artwork with very little effort. Further, it preserves the underlying geometry of the vector graphic primitives, thereby, making it easy to perform subsequent edits. Our method builds upon the concepts of shape coverage, color and opacity and thus is applicable to all vector graphics constructs including non-convex paths and text. Furthermore, our method is highly performant and provides real-time results irrespective of the number of coloring primitives used.
References:
- Simon Boyé, Pascal Barla, and Gaël Guennebaud. 2012. A Vectorial Solver for Freeform Vector Gradients. ACM Trans. Graph. 31, 6, Article 173 (Nov. 2012), 9 pages. https://doi.org/10.1145/2366145.2366192
- Alec Jacobson, Elif Tosun, Olga Sorkine, and Denis Zorin. 2010. Mixed finite elements for variational surface modeling. In Computer graphics forum, Vol. 29. Wiley Online Library, 1565–1574.
- Alexandrina Orzan, Adrien Bousseau, Holger Winnemöller, Pascal Barla, Joëlle Thollot, and David Salesin. 2008. Diffusion Curves: A Vector Representation for Smoothshaded Images. ACM Trans. Graph. 27, 3, Article 92 (Aug. 2008), 8 pages. https: //doi.org/10.1145/1360612.1360691
- Timothy Sun, Papoj Thamjaroenporn, and Changxi Zheng. 2014. Fast Multipole Representation of Diffusion Curves and Points. ACM Trans. Graph. 33, 4, Article 53 (July 2014), 12 pages. https://doi.org/10.1145/2601097.2601187
Keyword(s):
Additional Images: