“Frequency domain normal map filtering” by Han, Sun, Ramamoorthi and Grinspun

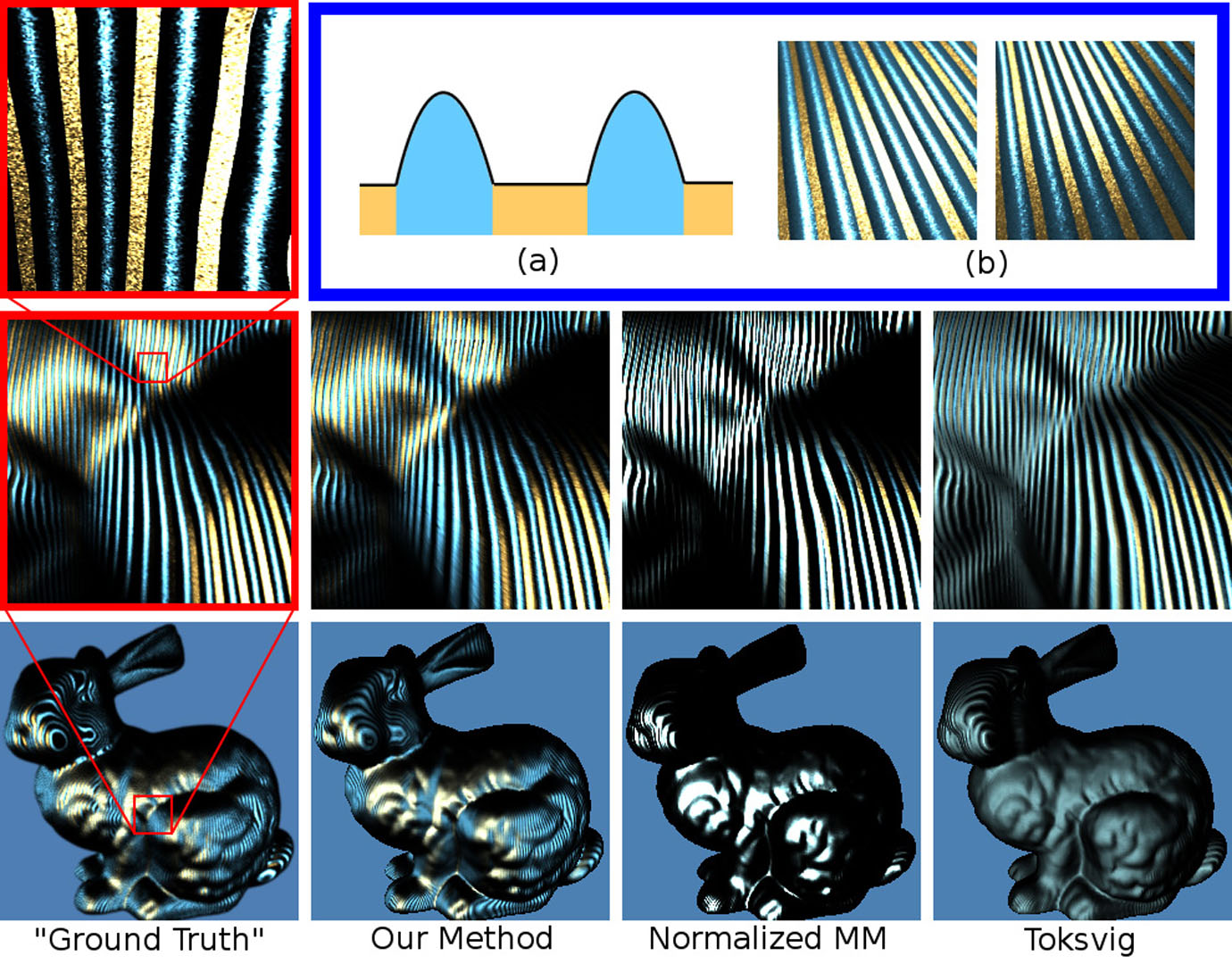
Filtering is critical for representing detail, such as color textures or normal maps, across a variety of scales. While MIP-mapping texture maps is commonplace, accurate normal map filtering remains a challenging problem because of nonlinearities in shading—we cannot simply average nearby surface normals. In this paper, we show analytically that normal map filtering can be formalized as a spherical convolution of the normal distribution function (NDF) and the BRDF, for a large class of common BRDFs such as Lambertian, microfacet and factored measurements. This theoretical result explains many previous filtering techniques as special cases, and leads to a generalization to a broader class of measured and analytic BRDFs. Our practical algorithms leverage a significant body of work that has studied lighting-BRDF convolution. We show how spherical harmonics can be used to filter the NDF for Lambertian and low-frequency specular BRDFs, while spherical von Mises-Fisher distributions can be used for high-frequency materials.

1. Banerjee, A., Dhillon, I., Ghosh, J., and Sra, S. 2005. Clustering on the unit hypersphere using von Mises-Fisher distributions. Journal of Machine Learning Research 6, 1345–1382. Google ScholarDigital Library
2. Basri, R., and Jacobs, D. 2001. Lambertian reflectance and linear subspaces. In International Conference on Computer Vision, 383–390.Google Scholar
3. Becker, B., and Max, N. 1993. Smooth transitions between bump rendering algorithms. In SIGGRAPH 93, 183–190. Google ScholarDigital Library
4. Blinn, J. 1978. Simulation of wrinkled surfaces. In SIGGRAPH 78, 286–292. Google ScholarDigital Library
5. Claustres, L., Barthe, L., and Paulin, M. 2007. Wavelet Encoding of BRDFs for Real-Time Rendering. In Graphics Interface 07. Google ScholarDigital Library
6. Cohen, J., Olano, M., and Manocha, D. 1998. Appearance preserving simplification. In SIGGRAPH 98, 115–122. Google ScholarDigital Library
7. Dempster, A., Laird, N., and Rubin, D. 1977. Maximum-likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society, Series B 39, 1–38.Google ScholarCross Ref
8. Fisher, R. 1953. Dispersion on a sphere. Proceedings of the Royal Society of London, Series A 217, 295–305.Google ScholarCross Ref
9. Fournier, A. 1992. Normal distribution functions and multiple surfaces. In Graphics Interface Workshop on Local Illumination, 45–52.Google Scholar
10. Hara, K., Nishino, K., and Ikeuchi, K. 2005. Multiple light sources and reflectance property estimation based on a mixture of spherical distributions. In ICCV ’05: Proceedings of the Tenth IEEE International Conference on Computer Vision, 1627–1634. Google ScholarDigital Library
11. Heckbert, P. 1989. Fundamentals of texture mapping and image warping. Master’s thesis, UC Berkeley UCB/CSD 89/516. Google ScholarDigital Library
12. Hochbaum, D., and Shmoys, D. 1985. A best possible heuristic for the k-center problem. Mathematics of Operations Research.Google Scholar
13. Horn, B. K. P. 1984. Extended gaussian images. Proceedings of the IEEE 72, 1671–1686.Google ScholarCross Ref
14. Kajiya, J. 1985. Anisotropic reflection models. In SIGGRAPH 85, 15–21. Google ScholarDigital Library
15. Lalonde, P., and Fournier, A. 1997. A wavelet representation of reflectance functions. IEEE TVCG 3, 4, 329–336. Google ScholarDigital Library
16. Lawrence, J., BenArtzi, A., Decoro, C., Matusik, W., Pfister, H., Ramamoorthi, R., and Rusinkiewicz, S. 2006. Inverse shade trees for non-parametric material representation and editing. ACM Transactions on Graphics (SIGGRAPH 2006) 25, 3, 735–745. Google ScholarDigital Library
17. Matusik, W., Pfister, H., Brand, M., and McMillan, L. 2003. A data-driven reflectance model. ACM Transactions on Graphics (SIGGRAPH 03 proceedings) 22, 3, 759–769. Google ScholarDigital Library
18. Ng, R., Ramamoorthi, R., and Hanrahan, P. 2004. Triple product wavelet integrals for all-frequency relighting. ACM Transactions on Graphics (SIGGRAPH 2004) 23, 3, 475–485. Google ScholarDigital Library
19. Olano, M., and North, M. 1997. Normal distribution mapping. Tech. Rep. 97-041 http://www.cs.unc.edu/~olano/papers/ndm/ndm.pdf, UNC.Google Scholar
20. Ramamoorthi, R., and Hanrahan, P. 2001. A signal-processing framework for inverse rendering. In SIGGRAPH 01, 117–128. Google ScholarDigital Library
21. Schilling, A. 1997. Toward real-time photorealistic rendering: Challenges and solutions. In SIGGRAPH/Eurographics Workshop on Graphics Hardware, 7–16. Google ScholarDigital Library
22. Sloan, P., Kautz, J., and Snyder, J. 2002. Precomputed radiance transfer for real-time rendering in dynamic, low-frequency lighting environments. ACM Transactions on Graphics (SIGGRAPH 02 proceedings) 21, 3, 527–536. Google ScholarDigital Library
23. Sloan, P., Luna, B., and Snyder, J. 2005. Local, deformable precomputed radiance transfer. ACM Transactions on Graphics (SIGGRAPH 05 proceedings) 24, 3, 1216–1224. Google ScholarDigital Library
24. Strehl, A., Ghosh, J., and Mooney, R. 2000. Impact of similarity measures on web-page clustering. In Proc Natl Conf on Artificial Intelligence: Workshop of AI for Web Search (AAAI 2000), 58–64.Google Scholar
25. Sun, B., Sunkavalli, K., Ramamoorthi, R., Belhumeur, P., and Nayar, S. 2007. Time-Varying BRDFs. IEEE Transactions on Visualization and Computer Graphics 13, 3, 595–609. Google ScholarDigital Library
26. Tan, P., Lin, S., Quan, L., Guo, B., and Shum, H. 2005. Multiresolution reflectance filtering. In EuroGraphics Symposium on Rendering 2005, 111–116. Google ScholarCross Ref
27. Toksvig, M. 2005. Mipmapping normal maps. Journal of Graphics Tools 10, 3, 65–71.Google ScholarCross Ref
28. Tsai, Y., and Shih, Z. 2006. All-frequency precomputed radiance transfer using spherical radial basis functions and clustered tensor approximation. ACM Transactions on Graphics (SIGGRAPH 2006) 25, 3, 967–976. Google ScholarDigital Library
29. Williams, L. 1983. Pyramidal parametrics. In SIGGRAPH 83, 1–11. Google ScholarDigital Library