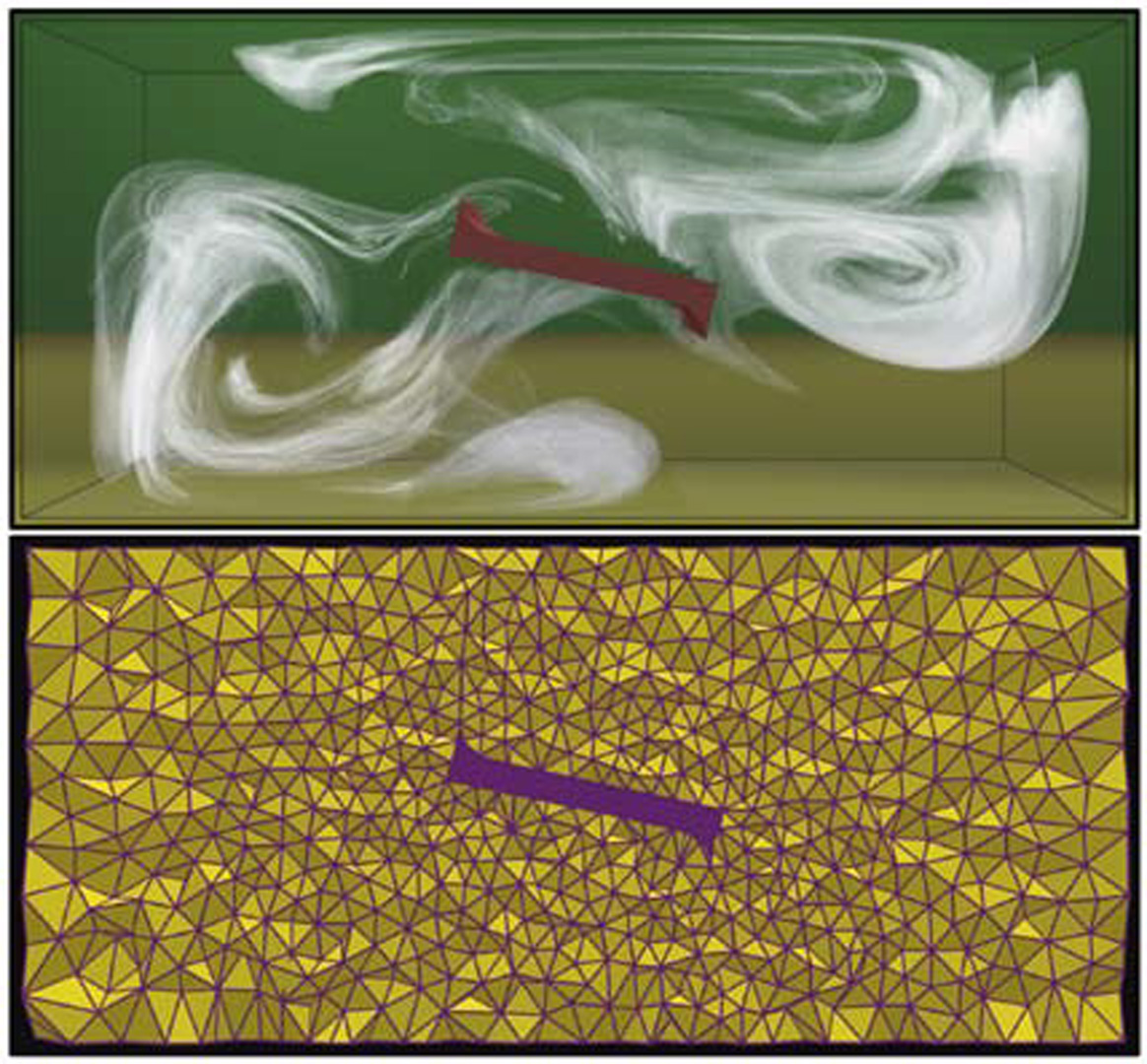
“Fluid animation with dynamic meshes” by Klingner, Feldman, Chentanez and O’Brien

This paper presents a method for animating fluid using unstructured tetrahedral meshes that change at each time step. We show that meshes that conform well to changing boundaries and that focus computation in the visually important parts of the domain can be generated quickly and reliably using existing techniques. We also describe a new approach to two-way coupling of fluid and rigid bodies that, while general, benefits from remeshing. Overall, the method provides a flexible environment for creating complex scenes involving fluid animation.

1. Alliez, P., Cohen-Steiner, D., Yvinec, M., and Desbrun, M. 2005. Variational tetrahedral meshing. In the Proceedings of ACM SIGGRAPH 2005, 617–625.]] Google ScholarDigital Library
2. Botta, N., and Hempel, D. 1996. A finite volume projection method for the numerical solution of the incompressible navier-stokes equations on triangular grids. First International Symposium on Finite Volumes for Complex Applications, 15–18 (July), 355–363.]]Google Scholar
3. Cani, M.-P., and Desbrun, M. 1997. Animation of deformable models using implicit surfaces. IEEE Transactions on Visualization and Computer Graphics 3, 1 (Jan.), 39–50.]] Google ScholarDigital Library
4. Carlson, M., Mucha, P. J., Van Horn III, R. B., and Turk, G. 2002. Melting and flowing. In the ACM SIGGRAPH 2002 Symposium on Computer Animation, 167–174.]] Google ScholarDigital Library
5. Carlson, M., Mucha, P. J., and Turk, G. 2004. Rigid fluid: animating the interplay between rigid bodies and fluid. In the Proceedings of ACM SIGGRAPH 2004, 377–384.]] Google ScholarDigital Library
6. Desbrun, M., and Cani, M.-P. 1996. Smoothed particles: A new paradigm for animating highly deformable bodies. In Computer Animation and Simulation 1996, 61–76.]] Google ScholarDigital Library
7. Donea, J., Fasoli-Stella, P., and Giuliani, S. 1977. Lagrangian and eulerian finite element techniques for transient fluid-structure interaction problems. In Trans. 4th SMIRT Conf.]]Google Scholar
8. Donea, J., Huerta, A., Ponthot, J.-P., and Rodríguez-Ferran, A. 2004. The Encyclopedia of Computational Mechanics. John Wiley & Sons Inc., New York.]]Google Scholar
9. Elcott, S., Tong, Y., Kanso, E., Schröder, P., and Desbrun, M. 2005. Discrete, circulation-preserving, and stable simplicial fluids. Preprint, Caltech.]]Google Scholar
10. Enright, D. P., Marschner, S. R., and Fedkiw, R. P. 2002. Animation and rendering of complex water surfaces. In the Proceedings of ACM SIGGRAPH 2002, 736–744.]] Google ScholarDigital Library
11. Fedkiw, R., Stam, J., and Jensen, H. W. 2001. Visual simulation of smoke. In the Proceedings of ACM SIGGRAPH 2001, 15–22.]] Google ScholarDigital Library
12. Feldman, B. E., O’Brien, J. F., and Arikan, O. 2003. Animating suspended particle explosions. In the Proceedings of ACM SIGGRAPH 2003, 708–715.]] Google ScholarDigital Library
13. Feldman, B. E., O’Brien, J. F., and Klingner, B. M. 2005. Animating gases with hybrid meshes. In Proceedings of ACM SIGGRAPH 2005.]] Google ScholarDigital Library
14. Feldman, B. E., O’Brien, J. F., Klingner, B. M., and Goktekin, T. G. 2005. Fluids in deforming meshes. In ACM SIGGRAPH/Eurographics Symposium on Computer Animation 2005.]] Google ScholarDigital Library
15. Foster, N., and Fedkiw, R. 2001. Practical animation of liquids. In the Proceedings of ACM SIGGRAPH 2001, 23–30.]] Google ScholarDigital Library
16. Foster, N., and Metaxas, D. 1996. Realistic animation of liquids. In Graphics Interface 1996, 204–212.]] Google ScholarDigital Library
17. Foster, N., and Metaxas, D. 1997. Modeling the motion of a hot, turbulent gas. In the Proceedings of ACM SIGGRAPH 97, 181–188.]] Google ScholarDigital Library
18. Goktekin, T. G., Bargteil, A. W., and O’Brien, J. F. 2004. A method for animating viscoelastic fluids. In the Proceedings of ACM SIGGRAPH 2004, 463–468.]] Google ScholarDigital Library
19. Guendelman, E., Selle, A., Losasso, F., and Fedkiw, R. 2005. Coupling water and smoke to thin deformable and rigid shells. In the Proceedings of ACM SIGGRAPH 2005, 973–981.]] Google ScholarDigital Library
20. Harlow, F., and Welch, J. 1965. Numerical calculation of time-dependent viscous incompressible flow of fluid with a free surface. The Physics of Fluids 8, 2182–2189.]]Google ScholarCross Ref
21. Hirt, C., Amsden, A., and Cook, J. 1974. An arbitrary lagrangian-eulerian computing method for all flow speeds. Journal of Computational Physics 14, 227–253.]]Google ScholarCross Ref
22. Ju, T., Schaefer, S., Warren, J., and Desbrun, M. 2005. A geometric construction of coordinates for convex polyhedra using polar duals. In Eurographics Symposium on Geometry Processing 2005, 181–186.]] Google ScholarDigital Library
23. Losasso, F., Gibou, F., and Fedkiw, R. 2004. Simulating water and smoke with an octree data structure. In the Proceedings of ACM SIGGRAPH 2004, 457–462.]] Google ScholarDigital Library
24. Müller, M., Charypar, D., and Gross, M. 2003. Particle-based fluid simulation for interactive applications. In the ACM SIGGRAPH 2003 Symposium on Computer Animation, 154–159.]] Google ScholarDigital Library
25. Müller, M., Keiser, R., Nealen, A., Pauly, M., Gross, M., and Alexa, M. 2004. Point based animation of elastic, plastic and melting objects. In the ACM SIGGRAPH 2004 Symposium on Computer Animation, 141–151.]] Google ScholarDigital Library
26. Owen, S. J. 1998. A survey of unstructured mesh generation technology. In the 7th International Meshing Roundtable, 239–267.]]Google Scholar
27. Premože, S., Tasdizen, T., Bigler, J., Lefohn, A., and Whitaker, R. 2003. Particle-based simulation of fluids. Computer Graphics Forum 22, 3 (Sept.), 401–410.]]Google ScholarCross Ref
28. Rasmussen, N., Enright, D., Nguyen, D., Marino, S., Sumner, N., Geiger, W., Hoon, S., and Fedkiw, R. 2004. Directable photo-realistic liquids. In the ACM SIGGRAPH 2004 Symposium on Computer Animation, 193–202.]] Google ScholarDigital Library
29. Selle, A., Rasmussen, N., and Fedkiw, R. 2005. A vortex particle method for smoke, water, and explosions. In the Proceedings of ACM SIGGRAPH 2005, 910–914.]] Google ScholarDigital Library
30. Shah, M., Cohen, J., Patel, S., Lee, P., and Pighin, F. 2004. Extended galilean invariance for adaptive fluid simulation. In 2004 ACM SIGGRAPH / Eurographics Symposium on Computer Animation, 13 — 221.]] Google ScholarDigital Library
31. Stam, J. 1999. Stable fluids. In the Proceedings of ACM SIGGRAPH 99, 121–128.]] Google ScholarDigital Library
32. Stora, D., Agliati, P.-O., Cani, M.-P., Neyret, F., and Gascuel, J.-D. 1999. Animating lava flows. In Graphics Interface 99, 203–210.]] Google ScholarDigital Library
33. Teng, S.-H., and Wong, C. W. 2000. Unstructured mesh generation: Theory, practice, and perspectives. International journal of computational geometry applications 10, 3, 227–266.]]Google Scholar
34. Terzopoulos, D., Platt, J., and Fleischer, K. 1989. Heating and melting deformable models (from goop to glop). In Graphics Interface 1989, 219–226.]]Google Scholar
35. Warren, J., Schaefer, S., Hirani, A. N., and Desbrun, M. 2004. Barycentric coordinates for convex sets. To appear in Advances in Computational and Applied Mathematics.]]Google Scholar
36. Yngve, G. D., O’Brien, J. F., and Hodgins, J. K. 2000. Animating explosions. In the Proceedings of ACM SIGGRAPH 2000, 29–36.]] Google ScholarDigital Library