“Flower modeling via X-ray computed tomography” by Ijiri, Yoshizawa, Yokota and Igarashi
Conference:
Type(s):
Title:
- Flower modeling via X-ray computed tomography
Session/Category Title:
- Points & Reconstruction
Presenter(s)/Author(s):
Abstract:
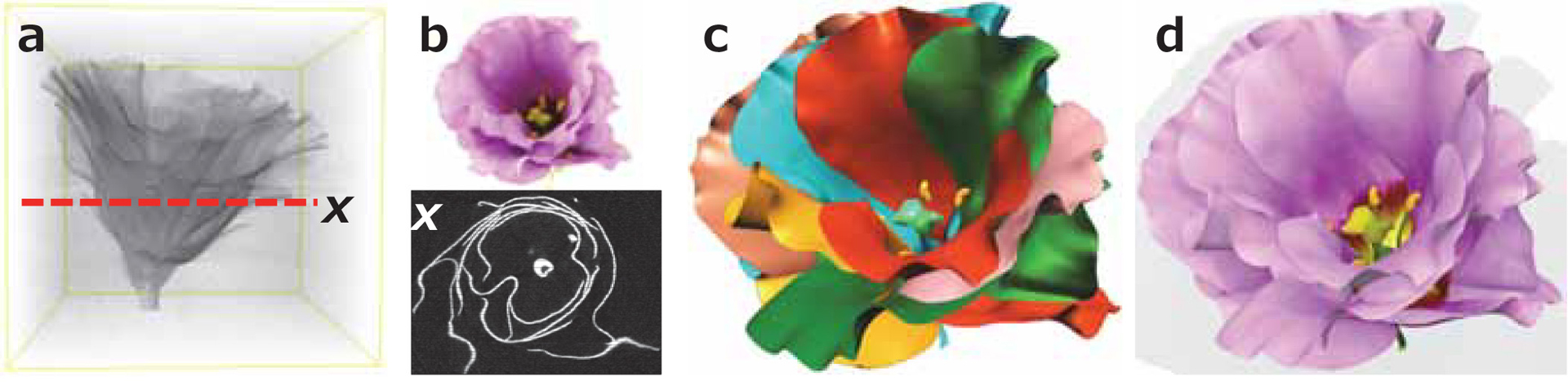
This paper presents a novel three dimensional (3D) flower modeling technique that utilizes an X-ray computed tomography (CT) system and real-world flowers. Although a CT system provides volume data that captures the internal structures of flowers, it is difficult to accurately segment them into regions of particular organs and model them as smooth surfaces because a flower consists of thin organs that contact one another. We thus introduce a semi-automatic modeling technique that is based on a new active contour model with energy functionals designed for flower CT. Our key idea is to approximate flower components by two important primitives, a shaft and a sheet. Based on our active contour model, we also provide novel user interfaces and a numerical scheme to fit these primitives so as to reconstruct realistic thin flower organs efficiently. To demonstrate the feasibility of our technique, we provide various flower models reconstructed from CT volumes.
References:
1. Abeysinghe, S., and Ju, T. 2009. Interactive skeletonization of intensity volumes. The Vis. Comput. 25, 5–7, 627–6354. Google ScholarDigital Library
2. Adams, R., and Bischof, L. 1994. Seeded region growing. IEEE Trans. PAML 16, 6, 641–647. Google ScholarDigital Library
3. Amenta, N., Bern, M., and Kamvysselis, M. 1998. A new voronoi-based surface reconstruction algorithm. In Proc. SIGGRAPH ’98. 415–421. Google ScholarDigital Library
4. Anastacio, F., Prusinkiewicz, P., and Sousa, M. 2009. Sketch-based parameterization of L-systems using illustration-inspired construction lines and depth modulation. Comput. Graph. 33, 4, 440–451. Google ScholarDigital Library
5. Bessmeltsev, M., Wang, C., Sheffer, A., and Singh, K. 2012. Design-driven quadrangulation of closed 3D curves. ACM Trans. Graph. 31, 5. Google ScholarDigital Library
6. Blum, H. 1967. A Transformation for Extracting New Descriptors of Shape. In Models for the Perception of Speech and Visual Form, W. Wathen-Dunn, Ed. MIT Press, Cambridge, 362–380.Google Scholar
7. Boykov, Y., and Jolly, M.-P. 2001. Interactive graph cuts for optimal boundary & region segmentation of objects in N-D images. In Proc. ICCV, vol. 1, 105–112.Google Scholar
8. Bradley, D., Nowrouzezahrai, D., and Beardsley, P. 2013. Image-based reconstruction and synthesis of dense foliage. ACM Trans. Graph. 32, 4, 74:1–74:10. Google ScholarDigital Library
9. Caselles, V., Kimmel, R., and Sapiro, G. 1997. Geodesic active contours. IJCV 22, 1, 61–79. Google ScholarDigital Library
10. Cohen, L., and Cohen, I. 1993. Finite element methods for active contour models and balloons for 2D and 3D images. IEEE Trans. PAMI 15, 1131–1147. Google ScholarDigital Library
11. Dijkstra, E. 1959. A note on two problems in connexion with graphs. Numer. Math. 1, 269–271. Google ScholarDigital Library
12. Eckstein, I., Pons, J.-P., Tong, Y., Kuo, J., and Desbrun, M. 2007. Generalized surface flows for mesh processing. In Proc. SGP, 183–192. Google ScholarDigital Library
13. Glimn-Lacy, J., and Kaufman, P. 2006. Botany Illustrated: Introduction to Plants, Major Groups, Flowering Plant Families. Springer.Google Scholar
14. Gregson, J., Krimerman, M., Hullin, M., and Heidrich, W. 2012. Stochastic tomography and its applications in 3D imaging of mixing fluids. ACM Trans. Graph. 31, 4. Google ScholarDigital Library
15. Huang, H., Wu, S., Cohen-Or, D., Gong, M., Zhang, H., Li, G., and Chen, B. 2013. L1-medial skeleton of point cloud. ACM Trans. Graph. 32, 65:1–65:8. Google ScholarDigital Library
16. Ijiri, T., Owada, S., Okabe, M., and Igarashi, T. 2005. Floral diagrams and inflorescences: Interactive flower modeling using botanical structural constraints. ACM Trans. Graph. 24, 3, 720–726. Google ScholarDigital Library
17. Ijiri, T., Yoshizawa, S., Sato, Y., Ito, M., and Yokota, H. 2013. Bilateral Hermite radial basis functions for contour-based volume segmentation. Comput. Graph. Forum 32, 2, 123–132.Google ScholarCross Ref
18. Ijiri, T., 2014. Flower CT volume and surface model library. www.riken.jp/brict/Ijiri/flowerctlib/.Google Scholar
19. Kass, M., Witkin, A., and Terzopoulos, D. 1988. Snakes: Active contour models. IJCV 1, 4, 321–331.Google ScholarCross Ref
20. Kazhdan, M., and Hoppe, H. 2013. Screened poisson surface reconstruction. ACM Trans. Graph. 32, 3, 29:1–29:13. Google ScholarDigital Library
21. Kobbelt, L., Campagna, S., Vorsatz, J., and Seidel, H.-P. 1998. Interactive multi-resolution modeling on arbitrary meshes. In Proc. ACM SIGGRAPH’98, 105–114. Google ScholarDigital Library
22. Li, Y., Fan, X., Mitra, N., Chamovitz, D., Cohen-Or, D., and Chen, B. 2013. Analyzing growing plants from 4D point cloud data. ACM Trans. Graph. 32, 6, 157:1–157:10. Google ScholarDigital Library
23. Lindenmayer, A. 1968. Mathematical models for cellular interaction in development: Parts I and II. J. Theor. Bio. 18.Google Scholar
24. Lintermann, B., and Deussen, O. 1999. Interactive modeling of plants. IEEE Comput. Graph Appl. 19, 1, 56–65. Google ScholarDigital Library
25. Longay, S., Runions, A., Boudon, F., and Prusinkiewicz, P. 2012. Treesketch: Interactive procedural modeling of trees on a tablet. In Proc. SBIM, 107–120. Google ScholarDigital Library
26. Lorensen, W., and Cline, H. 1987. Marching cubes: A high resolution 3D surface construction algorithm. Comput. Graph. 21, 4, 163–169. Google ScholarDigital Library
27. Moreton, H. P., and Séquin, C. H. 1992. Functional optimization for fair surface design. Comput. Graph. 26, 2, 167–176. Google ScholarDigital Library
28. Měch, R., and Prusinkiewicz, P. 1996. Visual models of plants interacting with their environment. In Proc. SIGGAPH ’96, 397–410. Google ScholarDigital Library
29. Nealen, A., Igarashi, T., Sorkine, O., and Alexa, M. 2007. Fibermesh: Designing freeform surfaces with 3D curves. ACM Trans. Graph. 26, 3, 41:1–41:10. Google ScholarDigital Library
30. Ohtake, Y., and Belyaev, A. 2001. Mesh optimization for polygonized isosurfaces. Comput. Graph. Forum 20, 3, 368–376.Google ScholarCross Ref
31. Okabe, M., Owada, S., and Igarashi, T. 2005. Interactive design of botanical trees using freehand sketches and example-based editing. Comput. Graph. Forum 24, 3, 487–496.Google ScholarCross Ref
32. Osher, S., and Sethian, J. 1988. Fronts propagating with curvature dependent speed: Algorithms based on Hamilton-Jacobi formulations. J. Comput. Phy. 79, 1, 12–49. Google ScholarDigital Library
33. Palubicki, W., Horel, K., Longay, S., Runions, A., Lane, B., Měch, R., and Prusinkiewicz, P. 2009. Self-organizing tree models for image synthesis. ACM Trans. Graph. 28, 3, 58:1–58:10. Google ScholarDigital Library
34. Prusinkiewicz, P., and Lindenmayer, A. 1990. The Algorithmic Beauty of Plants. Springer-Verlag New York, Inc. Google ScholarDigital Library
35. Prusinkiewicz, P., James, M., and Měch, R. 1994. Synthetic topiary. In Proc. SIGGRAPH ’94, 351–358. Google ScholarDigital Library
36. Prusinkiewicz, P., Mündermann, L., Karwowski, R., and Lane, B. 2001. The use of positional information in the modeling of plants. In Proc. SIGGRAPH ’01, 289–300. Google ScholarDigital Library
37. Quan, L., Tan, P., Zeng, G., Yuan, L., Wang, J., and Kang, S. 2006. Image-based plant modeling. ACM Trans. Graph. 25, 3, 599–604. Google ScholarDigital Library
38. Reche-Martinez, A., Martin, I., and Drettakis, G. 2004. Volumetric reconstruction and interactive rendering of trees from photographs. ACM Trans. Graph. 23, 3, 720–727. Google ScholarDigital Library
39. Sauvola, J., and Pietikäinen, M. 2000. Adaptive document image binarization. Pattern Recognit. 33, 225–236.Google ScholarCross Ref
40. Sethian, J. 1999. Level Set Methods and Fast Marching Methods. Cambridge University Press.Google Scholar
41. Sharf, A., Lewiner, T., Shamir, A., Kobbelt, L., and Cohen-Or, D. 2006. Competing fronts for coarse-to-fine surface reconstruction. Comput. Graph. Forum 25, 3, 389–398.Google ScholarCross Ref
42. Sochen, N., Kimmel, R., and Malladi, R. 1998. A general framework for low level vision. IEEE Trans. Image Proc. 7, 3, 310–318. Google ScholarDigital Library
43. Stuppy, W., Maisano, J., Colbert, M., Rudall, P., and Rowe, T. 2003. Three-dimensional analysis of plant structure using high-resolution X-ray computed tomography. Trends Plant Sci. 8, 1, 2–6.Google ScholarCross Ref
44. Süssmuth, J., and Greiner, G. 2007. Ridge based curve and surface reconstruction. In Proc. SGP, 243–251. Google ScholarDigital Library
45. Tan, P., Fang, T., Xiao, J., Zhao, P., and Quan, L. 2008. Single image tree modeling. ACM Trans. Graph. 27, 5, 108:1–108:7. Google ScholarDigital Library
46. Trifonov, B., Bradley, D., and Heidrich, W. 2006. Tomographic reconstruction of transparent objects. In Proc. EGSR, 51–60. Google ScholarDigital Library
47. Wood, Z., Schröder, P., Breen, D., and Desbrun, M. 2000. Semi-regular mesh extraction from volumes. In Proc. IEEE Vis, 275–282. Google ScholarDigital Library
48. Zhang, C., Ye, M., Fu, B., and Yang, R. 2014. Data-driven flower petal modeling with botany priors. In Proc. CVPR (to appear).Google Scholar
49. Zhao, S., Jakob, W., Marschner, S., and Bala, K. 2011. Building volumetric appearance models of fabric using micro CT imaging. ACM Trans. Graph. 30, 4, 44:1–44:10. Google ScholarDigital Library