“Flow aligned surfacing of curve networks” by Pan, Liu, Sheffer, Vining, Li, et al. …

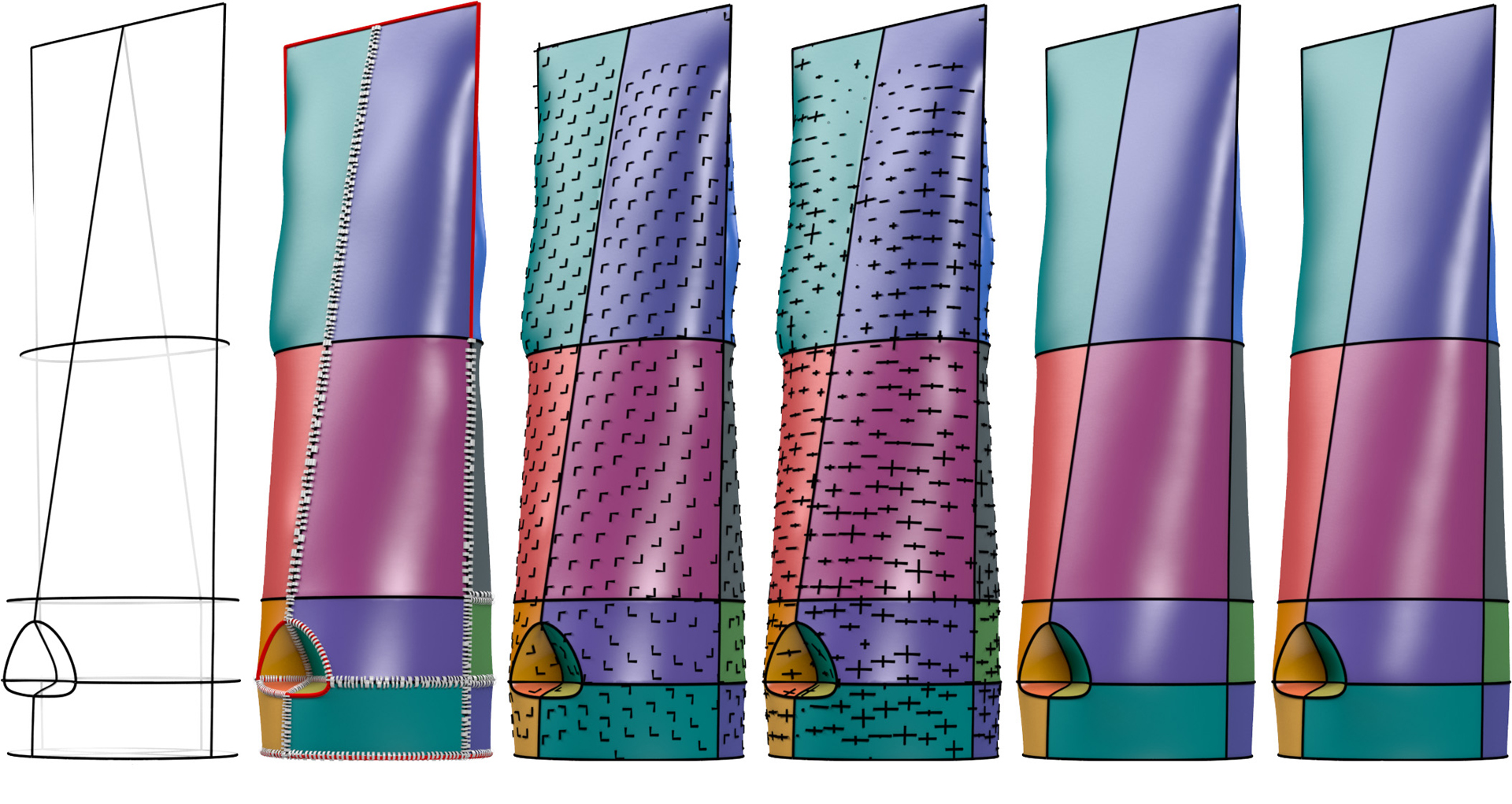
We propose a new approach for automatic surfacing of 3D curve networks, a long standing computer graphics problem which has garnered new attention with the emergence of sketch based modeling systems capable of producing such networks. Our approach is motivated by recent studies suggesting that artist-designed curve networks consist of descriptive curves that convey intrinsic shape properties, and are dominated by representative flow lines designed to convey the principal curvature lines on the surface. Studies indicate that viewers complete the intended surface shape by envisioning a surface whose curvature lines smoothly blend these flow-line curves. Following these observations we design a surfacing framework that automatically aligns the curvature lines of the constructed surface with the representative flow lines and smoothly interpolates these representative flow, or curvature directions while minimizing undesired curvature variation. Starting with an initial triangle mesh of the network, we dynamically adapt the mesh to maximize the agreement between the principal curvature direction field on the surface and a smooth flow field suggested by the representative flow-line curves. Our main technical contribution is a framework for curvature-based surface modeling, that facilitates the creation of surfaces with prescribed curvature characteristics. We validate our method via visual inspection, via comparison to artist created and ground truth surfaces, as well as comparison to prior art, and confirm that our results are well aligned with the computed flow fields and with viewer perception of the input networks.

1. Abbasinejad, F., Joshi, P., and Amenta, N. 2011. Surface patches from unorganized space curves. Comput. Graph. Forum (SGP) 30, 5, 1379–1387. Google ScholarDigital Library
2. Abbasinejad, F., Joshi, P., Grimm, C., Amenta, N., and Simons, L. 2013. Surface patches for 3D sketching. In Symp. on Sketch-Based Interfaces and Modeling, 53–60. Google ScholarDigital Library
3. Andrews, J., Joshi, P., and Carr, N. 2011. A linear variational system for modelling from curves. Comput. Graph. Forum (SGP) 30, 6, 1850–1861.Google ScholarCross Ref
4. Bae, S., Balakrishnan, R., and Singh, K. 2008. ILoveSketch: as-natural-as-possible sketching system for creating 3D curve models. In Symp. on UIST, 151–160. Google ScholarDigital Library
5. Bessmeltsev, M., Wang, C., Sheffer, A., and Singh, K. 2012. Design-driven quadrangulation of closed 3D curves. ACM Trans. Graph. (SIGGRAPH ASIA) 31, 6, 178:1–178:11. Google ScholarDigital Library
6. Biard, L., Farouki, R. T., and Szafran, N. 2010. Construction of rational surface patches bounded by lines of curvature. Comput. Aided Geom. Des. 27, 5, 359–371. Google ScholarDigital Library
7. Bo, P., Pottmann, H., Kilian, M., Wang, W., and Wallner, J. 2011. Circular arc structures. ACM Trans. Graph. (SIGGRAPH) 30, 4, 101:1–101:12. Google ScholarDigital Library
8. Bobenko, A., and Huhnen-Venedey, E. 2012. Curvature line parametrized surfaces and orthogonal coordinate systems: discretization with dupin cyclides. Geometriae Dedicata 159, 1, 207–237.Google ScholarCross Ref
9. Bobenko, A. I., and Schröder, P. 2005. Discrete Willmore flow. In Symp. on Geom. Proc., 101–110. Google ScholarDigital Library
10. Bobenko, A. I., and Suris, Y. B. 2008. Discrete Differential Geometry: Integrable Structure. AMS.Google Scholar
11. Bommes, D., Zimmer, H., and Kobbelt, L. 2009. Mixed-integer quadrangulation. ACM Trans. Graph. (SIGGRAPH ASIA) 28, 3, 77:1–77:10. Google ScholarDigital Library
12. Bordegoni, M., and Rizzi, C. 2011. Innovation in Product Design: From CAD to Virtual Prototyping. Springer.Google Scholar
13. Botsch, M., and Sorkine, O. 2008. On linear variational surface deformation methods. IEEE. T. Vis. Comput. Gr. 14, 1 (Jan), 213–230. Google ScholarDigital Library
14. Coons, S. 1964. Surfaces for computer aided design. Technical Report, MIT.Google Scholar
15. Crane, K., Pinkall, U., and Schröder, P. 2013. Robust fairing via conformal curvature flow. ACM Trans. Graph. (SIGGRAPH) 32, 4, 61:1–61:10. Google ScholarDigital Library
16. Das, K., Diaz-Gutierrez, P., and Gopi, M. 2005. Sketching free-form surfaces using network of curves. In Symp. on Sketch-Based Interfaces and Modeling.Google Scholar
17. Desbrun, M., Meyer, M., Schröder, P., and Barr, A. H. 1999. Implicit fairing of irregular meshes using diffusion and curvature flow. In SIGGRAPH, 317–324. Google ScholarDigital Library
18. Diamanti, O., Vaxman, A., Panozzo, D., and Sorkine-Hornung, O. 2014. Designing N-polyvector fields with complex polynomials. Comput. Graph. Forum (SGP) 33, 5, 1–11. Google ScholarDigital Library
19. Do Carmo, M. 1976. Differential Geometry of Curves and Surfaces. Prentice-Hall.Google Scholar
20. Dyer, R., Zhang, H., and Möller, T. 2007. Delaunay mesh construction. In Comput. Graph. Forum (SGP), 273–282. Google ScholarDigital Library
21. Eigensatz, M., Sumner, R. W., and Pauly, M. 2008. Curvature-domain shape processing. Comput. Graph. Forum (EG) 27, 2, 241–250.Google ScholarCross Ref
22. Farin, G., and Hansford, D. 1999. Discrete Coons patches. Comput. Aided Geom. Des. 16, 691–700. Google ScholarDigital Library
23. Finch, M., and Hoppe, H. 2011. Freeform vector graphics with controlled thin-plate splines. ACM Trans. Graph. (SIGGRAPH ASIA) 30, 6, 166:1–166:10. Google ScholarDigital Library
24. Gahan, A. 2010. 3D Automotive Modeling: An Insider’s Guide to 3D Car Modeling and Design for Games and Film. Elsevier Science.Google Scholar
25. Gao, K., and Rockwood, A. 2005. Multi-sided attribute based modeling. In Mathematics of Surfaces XI, 219–232. Google ScholarDigital Library
26. Joshi, P., and Séquin, C. H. 2007. Energy minimizers for curvature-based surface functionals. CAD Conference, 607–617.Google Scholar
27. Kälberer, F., Nieser, M., and Polthier, K. 2007. Quadcover – surface parameterization using branched coverings. Comput. Graph. Forum (SGP) 26, 3, 375–384.Google ScholarCross Ref
28. Kara, L. B., and Shimada, K. 2007. Sketch-based 3D-shape creation for industrial styling design. IEEE Comput. Graph. Appl. 27, 1, 60–71. Google ScholarDigital Library
29. Knöppel, F., Crane, K., Pinkall, U., and Schröder, P. 2013. Globally optimal direction fields. ACM Trans. Graph. (SIGGRAPH) 32, 4, 59:1–59:10. Google ScholarDigital Library
30. Levy, B. 2003. Dual domain extrapolation. ACM Trans. Graph. (SIGGRAPH) 22, 3, 364–369. Google ScholarDigital Library
31. Liu, Y., Pottmann, H., Wallner, J., Yang, Y.-L., and Wang, W. 2006. Geometric modeling with conical meshes and developable surfaces. ACM Trans. Graph. (SIGGRAPH) 25, 3, 681–689. Google ScholarDigital Library
32. Malraison, P. 2000. N-Sided Surfaces: a Survey. Defense Technical Information Center.Google Scholar
33. Martin, R. R., de Pont, J., and Sharrock, T. J. 1986. Cyclide surfaces in computer aided design. In Mathematics of Surfaces I. 253–268.Google Scholar
34. Nasri, A., Sabin, M., and Yasseen, Z. 2009. Filling N-sided regions by quad meshes for subdivision surfaces. Comput. Graph. Forum 28, 6, 1644–1658.Google ScholarCross Ref
35. Nealen, A., Igarashi, T., Sorkine, O., and Alexa, M. 2007. Fibermesh: Designing freeform surfaces with 3D curves. ACM Trans. Graph. (SIGGRAPH) 26, 3. Google ScholarDigital Library
36. Ray, N., Li, W. C., Lévy, B., Sheffer, A., and Alliez, P. 2006. Periodic global parameterization. ACM Trans. Graph. 25, 1460–1485. Google ScholarDigital Library
37. Ray, N., Vallet, B., Li, W. C., and Lévy, B. 2008. Nsymmetry direction field design. ACM Trans. Graph. 27, 2, 10:1–10:13. Google ScholarDigital Library
38. Rose, K., Sheffer, A., Wither, J., Cani, M.-P., and Thibert, B. 2007. Developable surfaces from arbitrary sketched boundaries. In Symp.on Geom. Proc., 163–172. Google ScholarDigital Library
39. Rusinkiewicz, S. 2004. Estimating curvatures and their derivatives on triangle meshes. In Symposium on 3D Data Processing, Visualization, and Transmission, 486–493. Google ScholarDigital Library
40. Sadri, B., and Singh, K. 2014. Flow-complex-based shape reconstruction from 3D curves. ACM Trans. Graph. 33, 2, 20:1–20:15. Google ScholarDigital Library
41. Schaefer, S., Warren, J., and Zorin, D. 2004. Lofting curve networks using subdivision surfaces. Symp. on Geom. Proc., 103. Google ScholarDigital Library
42. Schmidt, R., Khan, A., Singh, K., and Kurtenbach, G. 2009. Analytic drawing of 3D scaffolds. ACM Trans. Graph. (SIGGRAPH ASIA) 28, 5, 149:1–149:10. Google ScholarDigital Library
43. Schneider, R., and Kobbelt, L. 2001. Geometric fairing of irregular meshes for free-form surface design. Comput. Aided Geom. Des. 18, 4, 359–379. Google ScholarDigital Library
44. Singh, K., Pedersen, H., and Krishnamurthy, V. 2004. Feature based retargeting of parameterized geometry. In Geom. Model. Proc., 163–172. Google ScholarDigital Library
45. Sullivan, J. 2008. Curvatures of smooth and discrete surfaces. In Discrete Differential Geometry. 175–188.Google Scholar
46. Takayama, K., Panozzo, D., and Sorkine-Hornung, O. 2014. Pattern-based quadrangulation for N-sided patches. Comput. Graph. Forum (SGP) 33, 5, 177–184. Google ScholarDigital Library
47. Várady, T., Rockwood, A., and Salvi, P. 2011. Transfinite surface interpolation over irregular N-sided domains. Computer Aided Design 43, 11, 1330–1340. Google ScholarDigital Library
48. Wang, W., Jüttler, B., Zheng, D.-Y., and Liu, Y. 2008. Computation of rotation minimizing frame. ACM Trans. Graph. 27, 1, 2:1–2:18. Google ScholarDigital Library
49. Xu, B., Chang, W., Sheffer, A., Bousseau, A., McCrae, J., and Singh, K. 2014. True2Form: 3D curve networks from 2D sketches via selective regularization. ACM Trans. Graph. (SIGGRAPH) 33, 4, 131:1–131:13. Google ScholarDigital Library
50. Zhou, Q., Weinkauf, T., and Sorkine, O. 2011. Feature-based mesh editing. In Proc. Eurographics, Short Papers.Google Scholar
51. Zhuang, Y., Zou, M., Carr, N., and Ju, T. 2013. A general and efficient method for finding cycles in 3D curve networks. ACM Trans. Graph. (SIGGRAPH ASIA) 32, 6, 180:1–180:10. Google ScholarDigital Library
52. Zou, M., Ju, T., and Carr, N. 2013. An algorithm for triangulating multiple 3D polygons. Comput. Graph. Forum (SGP) 32, 5, 157–166. Google ScholarDigital Library