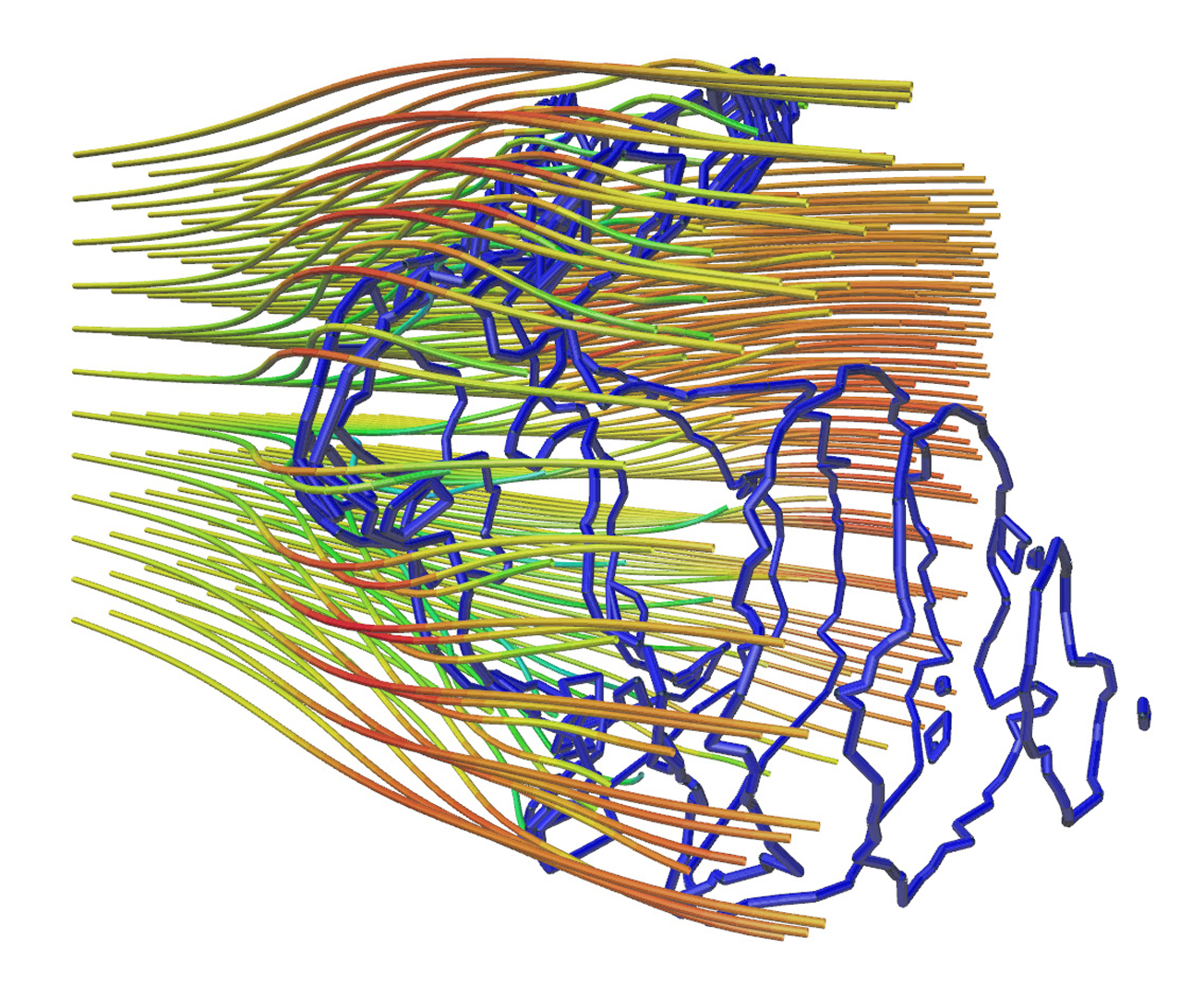
“Filament-based smoke with vortex shedding and variational reconnection” by Weißmann and Pinkall

Simulating fluids based on vortex filaments is highly attractive for the creation of special effects because it gives artists full control over the simulation using familiar tools like curve editors or the scripted generation of new vortex filaments over time. Because filaments offer a very compact description of fluid flow, real time applications like games or virtual reality are also possible.We present a complete model that includes moving obstacles with vortex shedding, all represented as filaments. Due to variational reconnection the long-time behavior of our method is excellent: Energy and momentum stay constant within reasonable bounds and computational complexity does not increase over time.

1. Angelidis, A., and Neyret, F. 2005. Simulation of Smoke based on Vortex Filament Primitives. In Proc. Symp. Comp. Anim., 87–96. Google ScholarDigital Library
2. Angelidis, A., Neyret, F., Singh, K., and Nowrouzezahrai, D. 2006. A controllable, fast and stable basis for vortex based smoke simulation. In Proc. Symp. Comp. Anim., 25–32. Google ScholarDigital Library
3. Angelidis, A. 2004. Hexanions: 6d Space for Twists. Tech. rep., University of Otago, November.Google Scholar
4. Becker, M., and Teschner, M. 2007. Weakly compressible SPH for free surface flows. In Proc. Symp. Comp. Anim., 209–217. Google ScholarDigital Library
5. Bernard, P. S. 2006. Turbulent flow properties of large-scale vortex systems. Proc. Natl. Acad. Sci. USA.Google ScholarCross Ref
6. Bernard, P. S. 2009. Vortex filament simulation of the turbulent coflowing jet. Phys. Fluids 21.Google Scholar
7. Börm, S., Grasedyck, L., and Hackbusch, W. 2003. Hierarchical Matrices. Lecture Notes. MPI MIS.Google Scholar
8. Chatelain, P., Curioni, A., Bergdorf, M., Rossinelli, D., Andreoni, W., and Koumoutsakos, P. 2008. Billion vortex particle direct numerical simulations of aircraft wakes. Comput. Methods Appl. Mech. Engrg. 197, 1296–1304.Google ScholarCross Ref
9. Chorin, A. J. 1990. Hairpin removal in vortex interactions. J. Comput. Phys. 91, 1, 1–21. Google ScholarDigital Library
10. Chorin, A. J. 1993. Hairpin Removal in Vortex Interactions II. J. Comput. Phys. 107, 1, 1–9. Google ScholarDigital Library
11. Crane, K., Llamas, I., and Tariq, S. 2007. GPU Gems 3 – Real-Time Simulation and Rendering of 3D Fluids. Addison-Wesley, ch. 30, 633–673.Google Scholar
12. Desbrun, M., and Gascuel, M.-P. 1996. Smoothed particles: a new paradigm for animating highly deformable bodies. In Symp. on Computer animation and simulation, Springer, 61–76. Google ScholarDigital Library
13. Desbrun, M., Kanso, E., and Tong, Y. 2008. Discrete Differential Forms for Computational Modeling. In Discrete Differential Geometry, vol. 38 of Oberwolfach Seminars. Birkhäuser.Google Scholar
14. Dormand, J. R., and Prince, P. J. 1980. A family of embedded Runge-Kutta formulae. Journal of Computational and Applied Mathematics 6, 1, 19–26.Google ScholarCross Ref
15. Dyke, M. V. 1982. An album of fluid motion. The parabolic Press, Stanford.Google Scholar
16. Elcott, S., Tong, Y., Kanso, E., Schröder, P., and Desbrun, M. 2007. Stable, circulation-preserving, simplicial fluids. ACM Trans. Graph. 26, 1. Google ScholarDigital Library
17. Fedkiw, R., Stam, J., and Jensen, H. W. 2001. Visual simulation of smoke. In Proc. ACM/SIGGRAPH Conf., 15–22. Google ScholarDigital Library
18. Greengard, C., and Anderson, C. R., Eds. 1988. Vortex Methods, vol. 1360 of Lecture Notes in Mathematics. Springer.Google Scholar
19. Katz, J., and Plotkin, A. 2001. Low-Speed Aerodynamics, 2 ed. No. 13 in Cambridge aerospace series. Cambridge Univ. Press.Google Scholar
20. Kim, B., Liu, Y., Llamas, I., and Rossignac, J. 2005. Flow-Fixer: Using BFECC for Fluid Simulation. In Proc. EG Workshop on Natural Phenomena, E. Galin and P. Poulin, Eds. Google ScholarDigital Library
21. Kim, T., Thürey, N., James, D., and Gross, M. 2008. Wavelet turbulence for fluid simulation. In Proc. ACM/SIGGRAPH Conf., 1–6. Google ScholarDigital Library
22. Kim, T. 2008. Hardware-aware analysis and optimization of stable fluids. In Proc. I3D Symp., 99–106. Google ScholarDigital Library
23. Krüger, J., and Westermann, R. 2005. GPU Simulation and Rendering of Volumetric Effects for Computer Games and Virtual Environments. Comp. Graph. Forum 24, 3.Google ScholarCross Ref
24. Lim, T. T., and Nickels, T. B. 1992. Instability and reconnection in the head-on collision of two vortex rings. Nature 357, 225–227.Google ScholarCross Ref
25. Lim, T. T. 1989. An experimental study of a vortex ring interacting with an inclined wall. Experiments in Fluids 7, 7 (July), 453–463.Google ScholarCross Ref
26. Marsden, J., and Weinstein, A. 1983. Coadjoint orbits, vortices, and Clebsch variables for incompressible fluids. Physica 7D, 305–323.Google Scholar
27. Marzouk, Y. M., and Ghoniem, A. F. 2007. Vorticity structure and evolution in a transverse jet. J. Fluid Mech. 575, 267–305.Google ScholarCross Ref
28. Mullen, P., Crane, K., Pavlov, D., Tong, Y., and Desbrun, M. 2009. Energy-preserving Integrators for Fluid Animation. Proc. ACM/SIGGRAPH Conf. 28, 3. Google ScholarDigital Library
29. Müller, M., Charypar, D., and Gross, M. 2003. Particle-based fluid simulation for interactive applications. In Proc. Symp. Comp. Anim., 154–159. Google ScholarDigital Library
30. Müller, M., Stam, J., James, D., and Thürey, N. 2008. Real time physics: class notes. In ACM/SIGGRAPH classes, 1–90. Google ScholarDigital Library
31. Narain, R., Sewall, J., Carlson, M., and Lin, M. C. 2008. Fast animation of turbulence using energy transport and procedural synthesis. ACM Trans. Graph. 27, 5, 1–8. Google ScholarDigital Library
32. Neyret, F. 2003. Advected Textures. In Proc. Symp. Comp. Anim. Google ScholarDigital Library
33. Park, S. I., and Kim, M. J. 2005. Vortex fluid for gaseous phenomena. In Proc. Symp. Comp. Anim., 261–270. Google ScholarDigital Library
34. Pfaff, T., Thuerey, N., Selle, A., and Gross, M. 2009. Synthetic turbulence using artificial boundary layers. In Proc. ACM/SIGGRAPH Asia Conf., 1–10. Google ScholarDigital Library
35. Pinkall, U., Springborn, B., and Weissmann, S. 2007. A new doubly discrete analogue of smoke ring flow and the real time simulation of fluid flow. J. Phys. A: Math. Theor. 40, 42, 12563–12576.Google ScholarCross Ref
36. Rasmussen, N., Nguyen, D. Q., Geiger, W., and Fedkiw, R. 2003. Smoke simulation for large scale phenomena. ACM Trans. Graph. 22, 3, 703–707. Google ScholarDigital Library
37. Rockliff, S. H. L., Peter Ryal Voke, and Nicole Jacqueline. 2000. Three-Dimensional Vortices of a Spatially Developing Plane Jet. International Journal of Fluid Dynamics 4, 1-+.Google Scholar
38. Saffman, P. G. 1992. Vortex Dynamics. Cambridge University Press, Cambridge.Google Scholar
39. Sato, K. 1999. Lévy Processes and Infinitely Divisible Distributions. Cambridge University Press.Google Scholar
40. Sauter, S., and Schwab, C. 2004. Randelementmethoden. Vieweg+Teubner.Google Scholar
41. Selle, A., Rasmussen, N., and Fedkiw, R. 2005. A vortex particle method for smoke, water and explosions. ACM Trans. Graph. 24, 3, 910–914. Google ScholarDigital Library
42. Stam, J., and Fiume, E. 1993. Turbulent wind fields for gaseous phenomena. In Proc. ACM/SIGGRAPH Conf., 369–376. Google ScholarDigital Library
43. Stam, J., and Fiume, E. 1995. Depicting fire and other gaseous phenomena using diffusion processes. In Proc. ACM/SIGGRAPH Conf., 129–136. Google ScholarDigital Library
44. Stam, J. 1999. Stable fluids. In Proc. ACM/SIGGRAPH Conf., 121–128. Google ScholarDigital Library
45. Treuille, A., Lewis, A., and Popović, Z. 2006. Model reduction for real-time fluids. ACM Trans. Graph. 25, 3, 826–834. Google ScholarDigital Library
46. Weiler, K. 1985. Edge-Based Data Structures for Solid Modeling in Curved-Surface Environments. Computer Graphics and Applications, IEEE 5, 1 (Jan.), 21–40. Google ScholarDigital Library
47. Weissmann, S., and Pinkall, U. 2009. Real-time interactive simulation of smoke using discrete integrable vortex filaments. In Proc. Vir. Real., Inter. & Phys. Sim., 1–10.Google Scholar
48. Weissmann, S., Gunn, C., Brinkmann, P., Hoffmann, T., and Pinkall, U. 2009. jReality. In Proc. ACM/MM Conf., 927–928. Google ScholarDigital Library
49. Yan, H., Wang, Z., He, J., Chen, X., Wang, C., and Peng, Q. 2009. Real-time fluid simulation with adaptive SPH. Computer Animation and Virtual Worlds 20, 2–3, 417–426. Google ScholarDigital Library
50. Yang, Q. 2009. Real-time simulation of 3D smoke based on Navier-Stokes equation. W. Trans. on Comp. 8, 1, 103–112. Google ScholarDigital Library