“Fast tile-based adaptive sampling with user-specified Fourier spectra” by Wachtel, Pilleboue, Coeurjolly, Breeden, Singh, et al. …

  • ©Florent Wachtel, Adrien Pilleboue, David Coeurjolly, Katherine Breeden, Gurprit Singh, Gaël Cathelin, Fernando de Goes, Mathieu Desbrun, and Victor Ostromoukhov

Conference:


Type:


Title:

    Fast tile-based adaptive sampling with user-specified Fourier spectra

Session/Category Title:   Sampling & Spectra

Presenter(s)/Author(s):


Moderator(s):


Abstract:


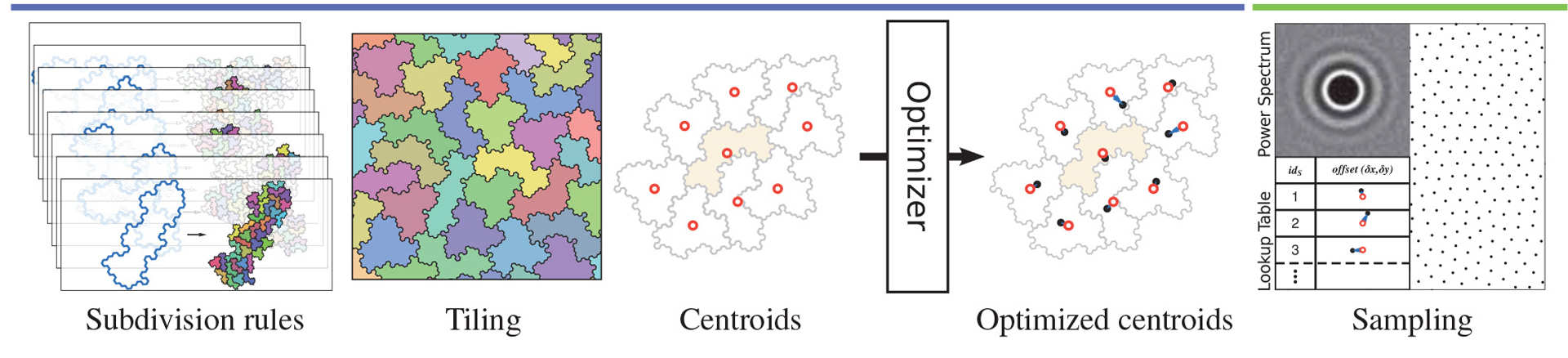
    We introduce a fast tile-based method for adaptive two-dimensional sampling with user-specified spectral properties. At the core of our approach is a deterministic, hierarchical construction of self-similar, equi-area, tri-hex tiles whose centroids have a spatial distribution free of spurious spectral peaks. A lookup table of sample points, computed offline using any existing point set optimizer to shape the samples’ Fourier spectrum, is then used to populate the tiles. The result is a linear-time, adaptive, and high-quality sampling of arbitrary density functions that conforms to the desired spectral distribution, achieving a speed improvement of several orders of magnitude over current spectrum-controlled sampling methods.

References:


    1. Balzer, M., Schlömer, T., and Deussen, O. 2009. Capacity-constrained point distributions: A variant of Lloyd’s method. ACM Trans. Graph. 28, 3, 86:1–8. Google ScholarDigital Library
    2. Belcour, L., Soler, C., Subr, K., Holzschuch, N., and Durand, F. 2013. 5D covariance tracing for efficient defocus and motion blur. ACM Trans. Graph. 32, 3, 31:1–31:18. Google ScholarDigital Library
    3. Chen, Z., Yuan, Z., Choi, Y.-K., Liu, L., and Wang, W. 2012. Variational blue noise sampling. IEEE Trans. Vis. Comput. Graphics 18, 10, 1784–1796. Google ScholarDigital Library
    4. Cohen, M., Shade, J., Hiller, S., and Deussen, O. 2003. Wang tiles for image and texture generation. ACM Trans. Graphics 22, 3, 287–294. Google ScholarDigital Library
    5. Conway, J. H., and Guy, R. K. 1996. The Book of Numbers. Springer-Verlag.Google Scholar
    6. Cook, R. L. 1986. Stochastic sampling in computer graphics. ACM Trans. Graph. 5, 1, 51–72. Google ScholarDigital Library
    7. de Goes, F., Breeden, K., Ostromoukhov, V., and Desbrun, M. 2012. Blue noise through optimal transport. ACM Trans. Graph. 31, 6, 171:1–171:10. Google ScholarDigital Library
    8. Dippé, M. A. Z., and Wold, E. H. 1985. Antialiasing through stochastic sampling. In ACM SIGGRAPH, 69–78. Google ScholarDigital Library
    9. Durand, F. 2011. A frequency analysis of Monte-Carlo and other numerical integration schemes. MIT CSAIL Technical report TR-2011-052.Google Scholar
    10. Ebeida, M. S., Davidson, A. A., Patney, A., Knupp, P. M., Mitchell, S. A., and Owens, J. D. 2011. Efficient maximal Poisson-disk sampling. ACM Trans. Graph. 30, 49:1–49:12. Google ScholarDigital Library
    11. Fattal, R. 2011. Blue-noise point sampling using kernel density model. ACM Trans. Graph. 30, 3, 48:1–48:12. Google ScholarDigital Library
    12. Gamito, M. N., and Maddock, S. C. 2009. Accurate multidimensional poisson-disk sampling. ACM Trans. Graph. 29, 8:1–8:19. Google ScholarDigital Library
    13. Grünbaum, B., and Shephard, G. C. 1986. Tilings and patterns. W. H. Freeman & Company. Google ScholarDigital Library
    14. Heck, D., Schlömer, T., and Deussen, O. 2013. Blue noise sampling with controlled aliasing. ACM Trans. Graph. 32, 3, 25:1–25:12. Google ScholarDigital Library
    15. Kopf, J., Cohen-Or, D., Deussen, O., and Lischinski, D. 2006. Recursive Wang tiles for real-time blue noise. ACM Trans. Graph. 25, 3, 509–518. Google ScholarDigital Library
    16. Kuipers, L., and Niederreiter, H. 1974. Uniform Distribution of Sequences. Dover Publications.Google Scholar
    17. Lagae, A., and Dutré, P. 2006. An Alternative for Wang Tiles: Colored Edges versus Colored Corners. ACM Trans. Graph. 25, 4, 1442–1459. Google ScholarDigital Library
    18. Lagae, A., Kaplan, C. S., Fu, C.-W., Ostromoukhov, V., and Deussen, O. 2008. Tile-based methods for interactive applications. In ACM SIGGRAPH 2008 classes, 93:1–93:267. Google ScholarDigital Library
    19. McCool, M., and Fiume, E. 1992. Hierarchical Poisson disk sampling distributions. In Proc. Graphics Interface ’92, 94–105. Google ScholarDigital Library
    20. Mitchell, D. 1991. Spectrally optimal sampling for distributed ray tracing. In ACM SIGGRAPH ’91, vol. 25, 157–164. Google ScholarDigital Library
    21. Ostromoukhov, V., Donohue, C., and Jodoin, P.-M. 2004. Fast hierarchical importance sampling with blue noise properties. ACM Trans. Graph. 23, 3, 488–495. Google ScholarDigital Library
    22. Ostromoukhov, V. 2007. Sampling with polyominoes. ACM Trans. Graph. 26, 3, 78:1–78:6. Google ScholarDigital Library
    23. Öztireli, A. C., and Gross, M. 2012. Analysis and synthesis of point distributions based on pair correlation. ACM Trans. Graph. 31, 6, 174:1–174:6. Google ScholarDigital Library
    24. Pharr, M., and Humphreys, G. 2010. Physically Based Rendering: From Theory to Implementation, 2nd ed. Morgan Kaufmann. Google ScholarDigital Library
    25. Pommerening, A. 2002. Approaches to quantifying forest structures. Forestry 75, 3, 305–324.Google ScholarCross Ref
    26. Schlömer, T., Heck, D., and Deussen, O. 2011. Farthest-point optimized point sets with maximized minimum distance. In Symp. on High Performance Graphics, 135–142. Google ScholarDigital Library
    27. Schmaltz, C., Gwosdek, P., Bruhn, A., and Weickert, J. 2010. Electrostatic halftoning. Comput. Graph. Forum 29, 8, 2313–2327.Google ScholarCross Ref
    28. Subr, K., and Kautz, J. 2013. Fourier analysis of stochastic sampling strategies for assessing bias and variance in integration. ACM Trans. Graph. 32, 4, 128:1–128:12. Google ScholarDigital Library
    29. Ulichney, R. A. 1988. Dithering with blue noise. Proc. of the IEEE 76, 56–79.Google ScholarCross Ref
    30. Ulichney, R. 1993. The void-and-cluster method for dither array generation. SPIE Vol. 1913, 332–343.Google Scholar
    31. Wang, H. 1965. Games, logic, and computers. Scientific American 213, 5, 98–106.Google ScholarCross Ref
    32. Wei, L.-Y., and Wang, R. 2011. Differential domain analysis for non-uniform sampling. ACM Trans. Graph. 30, 50:1–50:10. Google ScholarDigital Library
    33. Wei, L.-Y. 2008. Parallel Poisson disk sampling. ACM Trans. Graph. 27, 20:1–20:9. Google ScholarDigital Library
    34. Zhou, Y., Huang, H., Wei, L.-Y., and Wang, R. 2012. Point sampling with general noise spectrum. ACM Trans. Graph. 31, 4, 76:1–76:11. Google ScholarDigital Library

ACM Digital Library Publication:


Overview Page: