“Fast tetrahedral meshing in the wild” by Hu, Schneider, Wang, Zorin and Panozzo
Conference:
Type(s):
Title:
- Fast tetrahedral meshing in the wild
Session/Category Title: Cleaning Up the Mesh We Made
Presenter(s)/Author(s):
Moderator(s):
Abstract:
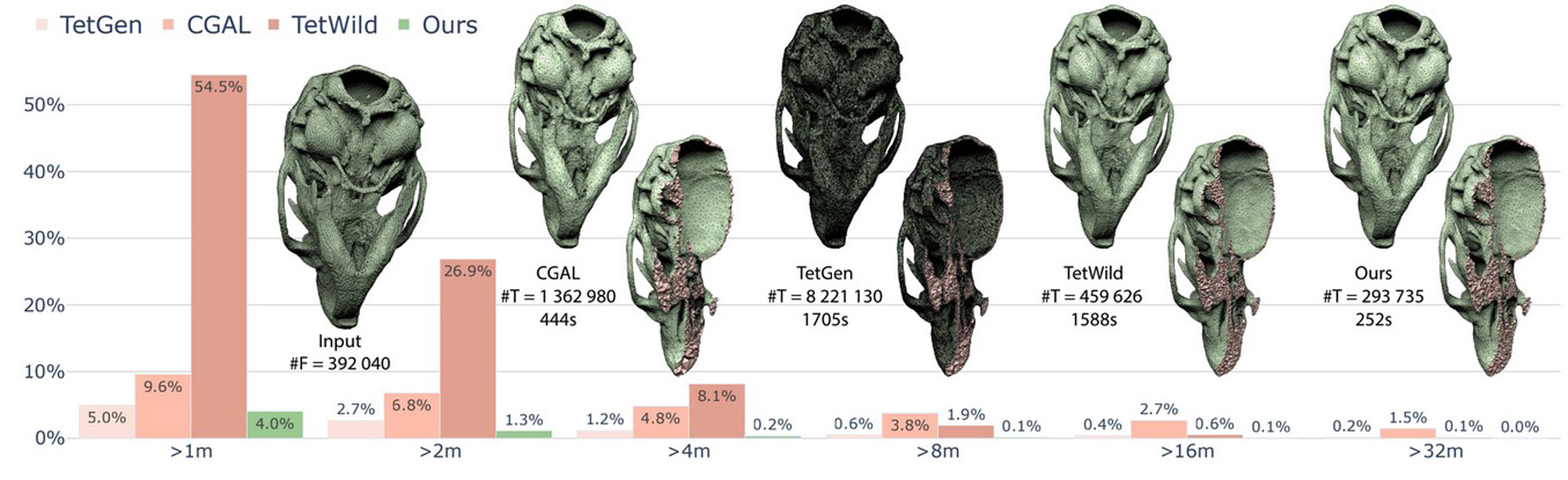
We propose a new tetrahedral meshing method, fTetWild, to convert triangle soups into high-quality tetrahedral meshes. Our method builds on the TetWild algorithm, replacing the rational triangle insertion with a new incremental approach to construct and optimize the output mesh, interleaving triangle insertion and mesh optimization. Our approach makes it possible to maintain a valid floating-point tetrahedral mesh at all algorithmic stages, eliminating the need for costly constructions with rational numbers used by TetWild, while maintaining full robustness and similar output quality. This allows us to improve on TetWild in two ways. First, our algorithm is significantly faster, with running time comparable to less robust Delaunay-based tetrahedralization algorithms. Second, our algorithm is guaranteed to produce a valid tetrahedral mesh with floating-point vertex coordinates, while TetWild produces a valid mesh with rational coordinates which is not guaranteed to be valid after floating-point conversion. As a trade-off, our algorithm no longer guarantees that all input triangles are present in the output mesh, but in practice, as confirmed by our tests on the Thingi10k dataset, the algorithm always succeeds in inserting all input triangles.
References:
1. L. A. Freitag and C. Ollivier-Gooch. 1998. Tetrahedral Mesh Improvement Using Swapping and Smoothing. Internat. J. Numer. Methods Engrg. 40 (05 1998).Google Scholar
2. F. Alauzet and D. Marcum. 2014. A Closed Advancing-Layer Method With Changing Topology Mesh Movement for Viscous Mesh Generation. In Proceedings of the 22nd International Meshing Roundtable. Springer International Publishing, Cham, 241–261.Google Scholar
3. M. Alexa. 2019. Harmonic Triangulations. ACM Transactions on Graphics (Proceedings of SIGGRAPH) 38, 4 (2019), 54.Google Scholar
4. P. Alliez, D. Cohen-Steiner, M. Yvinec, and M. Desbrun. 2005a. Variational Tetrahedral Meshing. ACM Transactions on Graphics 24, 3 (07 2005), 617. Google ScholarDigital Library
5. P. Alliez, D. Cohen-Steiner, M. Yvinec, and M. Desbrun. 2005b. Variational Tetrahedral Meshing. ACM Trans. Graph. 24, 3 (July 2005), 617–625. Google ScholarDigital Library
6. M. Attene. 2010. A lightweight approach to repairing digitized polygon meshes. The Visual Computer 26, 11 (01 Nov 2010), 1393–1406. Google ScholarDigital Library
7. M. Attene. 2014. Direct Repair of Self-intersecting Meshes. Graph. Models 76, 6 (Nov. 2014), 658–668. Google ScholarDigital Library
8. M. Attene. 2017. ImatiSTL – Fast and Reliable Mesh Processing with a Hybrid Kernel. Springer Berlin Heidelberg, Berlin, Heidelberg, 86–96.Google Scholar
9. M. Attene, M. Campen, and L. Kobbelt. 2013. Polygon Mesh Repairing: An Application Perspective. ACM Comput. Surv. 45, 2, Article 15 (March 2013), 33 pages.Google Scholar
10. M. Attene, D. Giorgi, M. Ferri, and B. Falcidieno. 2009. On converting sets of tetrahedra to combinatorial and PL manifolds. Computer Aided Geometric Design 26, 8 (2009), 850–864. Google ScholarDigital Library
11. F. Aurenhammer. 1991. Voronoi Diagrams—a Survey of a Fundamental Geometric Data Structure. ACM Comput. Surv. 23, 3 (Sept. 1991), 345–405. Google ScholarDigital Library
12. F. Aurenhammer, R. Klein, and D.-T. Lee. 2013. Voronoi Diagrams and Delaunay Triangulations. WORLD SCIENTIFIC, River Edge, NJ, USA. arXiv:https://www.worldscientific.com/doi/pdf/10.1142/8685 Google ScholarCross Ref
13. B. S. Baker, E. Grosse, and C. S. Rafferty. 1988. Nonobtuse triangulation of polygons. Discrete & Computational Geometry 3, 2 (01 Jun 1988), 147–168.Google Scholar
14. G. Barill, N. Dickson, R. Schmidt, D. I. Levin, and A. Jacobson. 2018. Fast Winding Numbers for Soups and Clouds. ACM Transactions on Graphics 37, 4 (2018), 43:1–43:12.Google ScholarDigital Library
15. H. Barki, G. Guennebaud, and S. Foufou. 2015. Exact, robust, and efficient regularized Booleans on general 3D meshes. Computers and Mathematics with Applications 70, 6 (2015), 1235–1254.Google ScholarDigital Library
16. M. Bern, D. Eppstein, and J. Gilbert. 1994. Provably good mesh generation. J. Comput. System Sci. 48, 3 (1994), 384–409.Google ScholarDigital Library
17. G. Bernstein. 2013. Cork Boolean Library. https://github.com/gilbo/cork.Google Scholar
18. G. Bernstein and D. Fussell. 2009. Fast, Exact, Linear Booleans. In SGP. Eurographics Association, Aire-la-Ville, Switzerland, Switzerland, 1269–1278.Google Scholar
19. H. Bieri and W. Nef. 1988. Elementary Set Operations with D-dimensional Polyhedra. In Proc. IWCGA. Springer-Verlag, Berlin, Heidelberg, 97–112.Google Scholar
20. C. J. Bishop. 2016. Nonobtuse Triangulations of PSLGs. Discrete & Computational Geometry 56, 1 (2016), 43–92.Google ScholarDigital Library
21. J.-D. Boissonnat, O. Devillers, S. Pion, M. Teillaud, and M. Yvinec. 2002. Triangulations in CGAL. Computational Geometry 22 (2002), 5–19.Google ScholarDigital Library
22. J.-D. Boissonnat and S. Oudot. 2005. Provably Good Sampling and Meshing of Surfaces. Graphical Models 67, 5 (09 2005), 405–451. Google ScholarDigital Library
23. R. Bridson and C. Doran. 2014. Quartet: A tetrahedral mesh generator that does isosurface stuffing with an acute tetrahedral tile. https://github.com/crawforddoran/quartet.Google Scholar
24. J. R. Bronson, J. A. Levine, and R. T. Whitaker. 2013. Lattice Cleaving: Conforming Tetrahedral Meshes of Multimaterial Domains With Bounded Quality. In Proceedings of the 21st International Meshing Roundtable. Springer Berlin Heidelberg, Berlin, Heidelberg, 191–209. Google ScholarCross Ref
25. O. Busaryev, T. K. Dey, and J. A. Levine. 2009. Repairing and Meshing Imperfect Shapes with Delaunay Refinement. In 2009 SIAM/ACM Joint Conference on Geometric and Physical Modeling (SPM ’09). ACM, 25–33.Google Scholar
26. M. Campen and L. Kobbelt. 2010. Exact and Robust (self-)intersections for Polygonal Meshes. Comput. Graph. Forum 29, 2 (2010), 397–406.Google ScholarCross Ref
27. S. A. Canann, S. N. Muthukrishnan, and R. K. Phillips. 1996. Topological refinement procedures for triangular finite element meshes. Engineering with Computers 12, 3 (01 Sep 1996), 243–255. Google ScholarCross Ref
28. S. A. Canann, M. B. Stephenson, and T. Blacker. 1993. Optismoothing: An optimization-driven approach to mesh smoothing. Finite Elements in Analysis and Design 13, 2 (1993), 185–190. Google ScholarDigital Library
29. L. Chen and J.-c. Xu. 2004. Optimal Delaunay Triangulations. Journal of Computational Mathematics 22, 2 (2004), 299–308.Google Scholar
30. S.-W. Cheng, T. K. Dey, and J. A. Levine. 2008. A Practical Delaunay Meshing Algorithm for a Large Class of Domains. In Proceedings of the 16th International Meshing Roundtable. Springer, Springer Berlin Heidelberg, Berlin, Heidelberg, 477–494.Google Scholar
31. S.-W. Cheng, T. K. Dey, and J. Shewchuk. 2012. Delaunay Mesh Generation. Chapman and Hall/CRC, Boca Raton, Florida.Google Scholar
32. L. P. Chew. 1989. Constrained delaunay triangulations. Algorithmica 4, 1 (01 Jun 1989), 97–108. Google ScholarCross Ref
33. L. P. Chew. 1993. Guaranteed-Quality Mesh Generation for Curved Surfaces. In Proceedings of the ninth annual symposium on Computational geometry – SCG ’93. ACM Press, New York, NY, USA, 274–280. Google ScholarDigital Library
34. D. Cohen-Steiner, E. C. de Verdière, and M. Yvinec. 2002. Conforming Delaunay Triangulations in 3D. In Proceedings of the eighteenth annual symposium on Computational geometry – SCG ’02. ACM Press, 217–233.Google Scholar
35. J.-C. Cuilliere, V. Francois, and J.-M. Drouet. 2013. Automatic 3D Mesh Generation of Multiple Domains for Topology Optimization Methods. In Proceedings of the 21st International Meshing Roundtable. Springer Berlin Heidelberg, Berlin, Heidelberg, 243–259. Google ScholarCross Ref
36. T. K. Dey and J. A. Levine. 2008. Delpsc: A Delaunay Mesher for Piecewise Smooth Complexes. In Proceedings of the twenty-fourth annual symposium on Computational geometry – SCG ’08. ACM Press, New York, NY, USA, 220–221. Google ScholarDigital Library
37. A. Doi and A. Koide. 1991. An efficient method of triangulating equi-valued surfaces by using tetrahedral cells. IEICE TRANSACTIONS on Information and Systems 74, 1 (1991), 214–224.Google Scholar
38. C. Doran, A. Chang, and R. Bridson. 2013. Isosurface Stuffing Improved: Acute Lattices and Feature Matching. In ACM SIGGRAPH 2013 Talks on – SIGGRAPH ’13. ACM Press, New York, NY, USA, 38:1–38:1. Google ScholarDigital Library
39. M. Douze, J.-S. Franco, and B. Raffin. 2015. QuickCSG: Arbitrary and Faster Boolean Combinations of N Solids. Technical Report 01121419. Inria Research Centre Grenoble, Rhone-Alpes.Google Scholar
40. Q. Du and D. Wang. 2003. Tetrahedral Mesh Generation and Optimization Based on Centroidal Voronoi Tessellations. International journal for numerical methods in engineering 56, 9 (2003), 1355–1373.Google Scholar
41. N. Faraj, J.-M. Thiery, and T. Boubekeur. 2016. Multi-Material Adaptive Volume Remesher. Compurer and Graphics Journal (proc. Shape Modeling International 2016) 58 (2016), 150–160.Google Scholar
42. L. Feng, P. Alliez, L. Busé, H. Delingette, and M. Desbrun. 2018. Curved Optimal Delaunay Triangulation. ACM Trans. Graph. 37, 4 (2018), 61:1–61:16.Google ScholarDigital Library
43. X. M. Fu, Y. Liu, and B. Guo. 2015. Computing Locally Injective Mappings by Advanced MIPS. ACM Trans. Graph. 34, 4, Article 71 (July 2015), 12 pages.Google ScholarDigital Library
44. J. A. George. 1971. Computer Implementation of the Finite Element Method. Ph.D. Dissertation. Stanford University, Stanford, CA, USA. AAI7205916.Google Scholar
45. P. L. George, H. Borouchaki, and E. Saltel. 2003. ‘Ultimate’ robustness in meshing an arbitrary polyhedron. Internat. J. Numer. Methods Engrg. 58, 7 (2003), 1061–1089.Google ScholarCross Ref
46. A. T. Ghomi, M. Bolhassan, A. Nejur, and M. Akbarzadeh. 2018. Effect of Subdivision of Force Diagrams on the Local Buckling, Load-Path and Material Use of Founded Forms. In Proceedings of the IASS Symposium 2018, Creativity in Structural Design. MIT, Boston, USA.Google Scholar
47. M. Granados, P. Hachenberger, S. Hert, L. Kettner, K. Mehlhorn, and M. Seel. 2003. Boolean operations on 3D selective Nef complexes: Data structure, algorithms, and implementation. In Proc. ESA. Springer Berlin Heidelberg, Berlin, Heidelberg, 654–666.Google Scholar
48. G. Guennebaud, B. Jacob, et al. 2010. Eigen v3.Google Scholar
49. P. Guigue and O. Devillers. 2003. Fast and Robust Triangle-Triangle Overlap Test Using Orientation Predicates. Journal of graphics tools 8, 1 (2003), 39–52. Google ScholarCross Ref
50. P. Hachenberger and L. Kettner. 2019. 3D Boolean Operations on Nef Polyhedra. In CGAL User and Reference Manual (4.14 ed.). CGAL Editorial Board.Google Scholar
51. R. Haimes. 2014. MOSS: Multiple Orthogonal Strand System. In Proceedings of the 22nd International Meshing Roundtable. Springer International Publishing, Cham, 75–91. Google ScholarCross Ref
52. K. Hu, D. Yan, D. Bommes, P. Alliez, and B. Benes. 2017. Error-Bounded and Feature Preserving Surface Remeshing with Minimal Angle Improvement. IEEE Transactions on Visualization and Computer Graphics 23, 12 (Dec 2017), 2560–2573.Google ScholarCross Ref
53. Y. Hu, T. Schneider, X. Gao, Q. Zhou, A. Jacobson, D. Zorin, and D. Panozzo. 2019. TriWild: Robust Triangulation with Curve Constraints. ACM Trans. Graph. (2019).Google Scholar
54. Y. Hu, Q. Zhou, X. Gao, A. Jacobson, D. Zorin, and D. Panozzo. 2018. Tetrahedral Meshing in the Wild. ACM Trans. Graph. 37, 4, Article 60 (July 2018), 14 pages. Google ScholarDigital Library
55. C. Jamin, P. Alliez, M. Yvinec, and J.-D. Boissonnat. 2015. CGALmesh: A Generic Framework for Delaunay Mesh Generation. ACM Trans. Math. Software 41, 4 (10 2015), 1–24. Google ScholarDigital Library
56. B. Klingner and J. Shewchuk. 2007. Aggressive Tetrahedral Mesh Improvement. Proceedings of the 16th International Meshing Roundtable, IMR 2007, 3–23.Google Scholar
57. F. Labelle and J. R. Shewchuk. 2007. Isosurface Stuffing: Fast Tetrahedral Meshes With Good Dihedral Angles. In ACM SIGGRAPH 2007 papers on – SIGGRAPH ’07. ACM Press, New York, NY, USA, 57. Google ScholarDigital Library
58. B. Lévy. 2019. Geogram. http://alice.loria.fr/index.php/software/4-library/75-geogram.html.Google Scholar
59. Y. Lipman. 2012. Bounded Distortion Mapping Spaces for Triangular Meshes. ACM Trans. Graph. 31, 4 (2012), 108.Google ScholarDigital Library
60. W. E. Lorensen and H. E. Cline. 1987. Marching Cubes: A High Resolution 3D Surface Construction Algorithm. SIGGRAPH Comput. Graph. 21, 4 (Aug. 1987), 163–169. Google ScholarDigital Library
61. S. V. Magalhães, W. R. Franklin, and M. V. Andrade. 2017. Fast exact parallel 3D mesh intersection algorithm using only orientation predicates. In Proceedings of the 25th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. ACM, ACM, New York, NY, USA, 44.Google Scholar
62. M. Mandad, D. Cohen-Steiner, and P. Alliez. 2015. Isotopic Approximation Within a Tolerance Volume. ACM Trans. Graph. 34, 4, Article 64 (July 2015), 12 pages. Google ScholarDigital Library
63. A. Masoud. 2016. 3D Graphical Statics Using Reciprocal Polyhedral Diagrams. Ph.D. Dissertation. ETH Zruich, Stefano Franscini Platz 5, Zurich, CH, 8093.Google Scholar
64. N. Molino, R. Bridson, and R. Fedkiw. 2003. Tetrahedral Mesh Generation for Deformable Bodies. In Proc. Symposium on Computer Animation.Google Scholar
65. M. Murphy, D. M. Mount, and C. W. Gable. 2001. A Point-Placement Strategy for Conforming Delaunay Tetrahedralization. International Journal of Computational Geometry & Applications 11, 06 (12 2001), 669–682.Google ScholarCross Ref
66. K. Museth, D. E. Breen, R. T. Whitaker, and A. H. Barr. 2002. Level set surface editing operators. ACM Trans. Graph. 21, 3 (2002), 330–338.Google ScholarDigital Library
67. B. Naylor, J. Amanatides, and W. Thibault. 1990. Merging BSP trees yields polyhedral set operations. In Proc. SIGGRAPH. ACM, New York, NY, USA, 115–124.Google Scholar
68. A. Paoluzzi, V. Shapiro, and A. DiCarlo. 2017. Arrangements of cellular complexes. CoRR abs/1704.00142 (2017). arXiv:1704.00142 http://arxiv.org/abs/1704.00142Google Scholar
69. D. Pavic, M. Campen, and L. Kobbelt. 2010. Hybrid Booleans. Comput. Graph. Forum 29 (2010), 75–87.Google ScholarCross Ref
70. J. Peraire, M. Vahdati, K. Morgan, and O. C. Zienkiewicz. 1987. Adaptive Remeshing for Compressible Flow Computations. J. Comput. Phys. 72, 2 (Oct. 1987), 449–466.Google ScholarDigital Library
71. M. Rabinovich, R. Poranne, D. Panozzo, and O. Sorkine-Hornung. 2017. Scalable Locally Injective Mappings. ACM Trans. Graph. 36, 2 (April 2017), 16.Google ScholarDigital Library
72. J.-F. Remacle. 2017. A Two-Level Multithreaded Delaunay Kernel. Computer-Aided Design 85 (04 2017), 2–9. Google ScholarDigital Library
73. J. Ruppert. 1995. A Delaunay Refinement Algorithm for Quality 2-Dimensional Mesh Generation. Journal of Algorithms 18, 3 (05 1995), 548–585. Google ScholarDigital Library
74. E. A. Sadek. 1980. A scheme for the automatic generation of triangular finite elements. Internat. J. Numer. Methods Engrg. 15, 12 (1980), 1813–1822.Google ScholarCross Ref
75. R. Schmidt and K. Singh. 2010. Meshmixer: an interface for rapid mesh composition. In ACM SIGGRAPH 2010 Talks. ACM, ACM, New York, NY, USA, 6.Google Scholar
76. T. Schneider, Y. Hu, J. Dumas, X. Gao, D. Panozzo, and D. Zorin. 2018. Decoupling simulation accuracy from mesh quality. ACM Transactions on Graphics 37, 6 (dec 2018), 1–14. Google ScholarDigital Library
77. M. Schweiger and S. Arridge. 2016. Basis mapping methods for forward and inverse problems: BASIS MAPPING METHODS. Internat. J. Numer. Methods Engrg. 109 (05 2016). Google ScholarCross Ref
78. D. R. Sheehy. 2012. New Bounds on the Size of Optimal Meshes. Computer Graphics Forum 31, 5 (08 2012), 1627–1635. Google ScholarDigital Library
79. C. Shen, J. F. O’Brien, and J. R. Shewchuk. 2004. Interpolating and Approximating Implicit Surfaces from Polygon Soup. In Proceedings of ACM SIGGRAPH 2004. ACM Press, 896–904.Google Scholar
80. B. Sheng, P. Li, H. Fu, L. Ma, and E. Wu. 2018a. Efficient non-incremental constructive solid geometry evaluation for triangular meshes. Graphical Models 97 (2018), 1–16.Google ScholarCross Ref
81. B. Sheng, B. Liu, P. Li, H. Fu, L. Ma, and E. Wu. 2018b. Accelerated robust Boolean operations based on hybrid representations. Computer Aided Geometric Design 62 (2018), 133–153.Google ScholarDigital Library
82. J. Shewchuk. 2012. Unstructured Mesh Generation. Chapman and Hall/CRC, Boca Raton, Florida, Chapter 10, 257–297.Google Scholar
83. J. R. Shewchuk. 1996. Triangle: Engineering a 2D quality mesh generator and Delaunay triangulator. In Applied Computational Geometry Towards Geometric Engineering, Ming C. Lin and Dinesh Manocha (Eds.). Springer Berlin Heidelberg, Berlin, Heidelberg, 203–222.Google ScholarDigital Library
84. J. R. Shewchuk. 1997. Adaptive Precision Floating-Point Arithmetic and Fast Robust Geometric Predicates. Discrete & Computational Geometry 18, 3 (Oct. 1997), 305–363.Google Scholar
85. J. R. Shewchuk. 1998. Tetrahedral Mesh Generation by Delaunay Refinement. In Proceedings of the fourteenth annual symposium on Computational geometry – SCG ’98. ACM Press, New York, NY, USA, 86–95. Google ScholarDigital Library
86. J. R. Shewchuk. 1999. Lecture Notes on Delaunay Mesh Generation. (1999).Google Scholar
87. J. R. Shewchuk. 2002a. Constrained Delaunay Tetrahedralizations and Provably Good Boundary Recovery. In Eleventh International Meshing Roundtable. Sandia National Laboratories, 193–204.Google Scholar
88. J. R. Shewchuk. 2002b. What is a good linear element? interpolation, conditioning, and quality measures. In In 11th International Meshing Roundtable. 115–126.Google Scholar
89. H. Si. 2015. TetGen, a Delaunay-Based Quality Tetrahedral Mesh Generator. ACM Trans. Math. Softw. 41, 2, Article 11 (Feb. 2015), 36 pages. Google ScholarDigital Library
90. H. Si and K. Gartner. 2005. Meshing Piecewise Linear Complexes by Constrained Delaunay Tetrahedralizations. In Proceedings of the 14th international meshing roundtable. Springer, Springer Berlin Heidelberg, Berlin, Heidelberg, 147–163.Google Scholar
91. H. Si and J. R. Shewchuk. 2014. Incrementally Constructing and Updating Constrained Delaunay Tetrahedralizations With Finite-Precision Coordinates. Engineering with Computers 30, 2 (04 2014), 253–269. Google ScholarDigital Library
92. K. Takayama, A. Jacobson, L. Kavan, and O. Sorkine-Hornung. 2014. A Simple Method for Correcting Facet Orientations in Polygon Meshes Based on Ray Casting. Journal of Computer Graphics Techniques 3, 4 (2014), 53–63.Google Scholar
93. W. C. Thibault and B. F. Naylor. 1987. Set operations on polyhedra using binary space partitioning trees. In Proc. SIGGRAPH. ACM, New York, NY, USA, 153–162.Google Scholar
94. J. Tournois, C. Wormser, P. Alliez, and M. Desbrun. 2009. Interleaving Delaunay Refinement and Optimization for Practical Isotropic Tetrahedron Mesh Generation. ACM Transactions on Graphics 28, 3 (07 2009), 1.Google ScholarDigital Library
95. G. Varadhan, S. Krishnan, T. Sriram, and D. Manocha. 2004. Topology preserving surface extraction using adaptive subdivision. In SGP. ACM, New York, NY, USA, 235–244.Google Scholar
96. B. Wang, T. Schneider, Y. Hu, M. Attene, and D. Panozzo. 2020. Exact and Efficient Polyhedral Envelope Containment Check. ACM Trans. Graph. 39, 4 (July 2020).Google ScholarDigital Library
97. C. C. L. Wang. 2011. Approximate Boolean Operations on Large Polyhedral Solids with Partial Mesh Reconstruction. IEEE Trans. Vis. Comput. Graph. 17, 6 (2011), 836–849.Google ScholarDigital Library
98. N. P. Weatherill and O. Hassan. 1994. Efficient three-dimensional Delaunay triangulation with automatic point creation and imposed boundary constraints. Internat. J. Numer. Methods Engrg. 37, 12 (1994), 2005–2039.Google ScholarCross Ref
99. R. Wein, E. Berberich, E. Fogel, D. Halperin, M. Hemmer, O. Salzman, and B. Zukerman. 2018. 2D Arrangements. In CGAL User and Reference Manual (4.13 ed.). CGAL Editorial Board.Google Scholar
100. M. A. Yerry and M. S. Shephard. 1983. A Modified Quadtree Approach To Finite Element Mesh Generation. IEEE Computer Graphics and Applications 3, 1 (Jan 1983), 39–46.Google ScholarDigital Library
101. H. Zhao, C. C. Wang, Y. Chen, and X. Jin. 2011. Parallel and efficient Boolean on polygonal solids. The Visual Computer 27, 6-8 (2011), 507–517.Google ScholarDigital Library
102. Q. Zhou, E. Grinspun, D. Zorin, and A. Jacobson. 2016. Mesh Arrangements for Solid Geometry. ACM Transactions on Graphics (TOG) 35, 4 (2016), 39.Google ScholarDigital Library
103. Q. Zhou and A. Jacobson. 2016. Thingi10K: A Dataset of 10, 000 3D-Printing Models. CoRR abs/1605.04797 (2016). arXiv:1605.04797Google Scholar