“Fast exact and approximate geodesics on meshes”

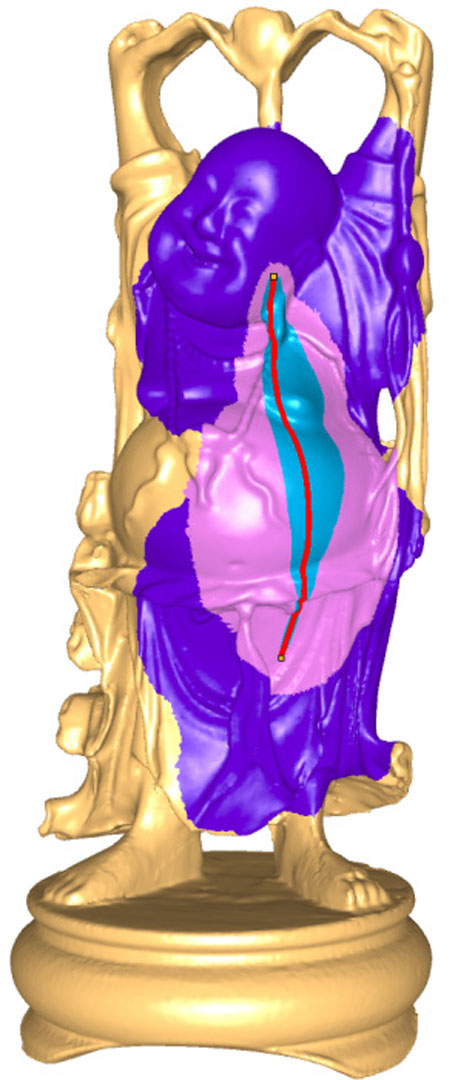
The computation of geodesic paths and distances on triangle meshes is a common operation in many computer graphics applications. We present several practical algorithms for computing such geodesics from a source point to one or all other points efficiently. First, we describe an implementation of the exact “single source, all destination” algorithm presented by Mitchell, Mount, and Papadimitriou (MMP). We show that the algorithm runs much faster in practice than suggested by worst case analysis. Next, we extend the algorithm with a merging operation to obtain computationally efficient and accurate approximations with bounded error. Finally, to compute the shortest path between two given points, we use a lower-bound property of our approximate geodesic algorithm to efficiently prune the frontier of the MMP algorithm. thereby obtaining an exact solution even more quickly.

1. Chen, J., and Han, Y. 1996. Shortest paths on a polyhedron; part I: computing shortest paths. Int. J. Comp. Geom. & Appl. 6 (2), 127–144.Google ScholarCross Ref
2. Floater, M. S., Hormann, K., and Reimers, M. 2002. Parameterization of manifold triangulations. Approx. Theory X: Abstract and Classical Analysis, Vanderbilt University Press, Nashville, 197–209.Google Scholar
3. Floater, M. S. 2005. Chordal cubic spline interpolation is fourth order accurate. IMA J. Numer Analysis. to appear.Google Scholar
4. Funkhouser, T., Kazhdan, M., Shilane, P., Min, P., Kiefer, W., Tal, A., Rusinkiewicz, S., and Dobkin, D. 2004. Modeling by example. In Proc. of SIGGRAPH 2004, 652–663. Google ScholarDigital Library
5. Goldberg, A. V., and Harrelson, C. 2005. Computing the shortest path: A* search meets graph theory. In Proc. of the 16th Annual ACMSIAM Symp. on Discrete Algorithms, 156–165. Google ScholarDigital Library
6. Hershberger, J. E., and Suri, S. 1999. An optimal algorithm for Euclidean shortest paths in the plane. Siam J. Comp. 28 (6) 2215–2256. Google ScholarDigital Library
7. Hilaga, M., Shinagawa, Y., Kohmura, T., and Kunii, T. L. 2001. Topology matching for fully automatic similarity estimation of 3d shapes. In Proc. of ACM SIGGRAPH 2001, 203–212. Google ScholarDigital Library
8. Kanai, T., and Suzuki, H. 2001. Approximate shortest path on a polyhedral surface and its applications. Comp. -Aided Design 33, 11, 801–811.Google ScholarCross Ref
9. Kaneva, B., and O’Rourke, J. 2000. An implementation of Chen & Han’s shortest paths algorithm. In Proc. of the 12th Canadian Conf. on Comput. Geom., 139–146.Google Scholar
10. Kapoor, S. 1999. Efficient computation of geodesic shortest paths. In Proc. 32nd Annual ACM Symp. Theory Comput., 770–779. Google ScholarDigital Library
11. Katz, S., and Tal, A. 2003. Hierarchical mesh decomposition using fuzzy clustering and cuts. ACM Trans. on Graphics 22, 3 (Jul), 954–961. Google ScholarDigital Library
12. Kimmel, R., and Sethian, J. A. 1998. Computing geodesic paths on manifolds. Proc. of National Academy of Sci. 95(15) (July), 8431–8435.Google ScholarCross Ref
13. Kirsanov, D. 2004. Minimal Discrete Curves and Surfaces. PhD thesis, Applied Math., Harvard University. Google ScholarDigital Library
14. Kobbelt, L., Campagna, S., Vorsatz, J., and Seidel, H.-P. 1998. Interactive multiresolution modeling on arbitrary meshes. In Proc. of SIGGRAPH 98, 105–114. Google ScholarDigital Library
15. Krishnamurthy, V., and Levoy, M. 1996. Fitting smooth surfaces to dense polygon meshes. In Proc. of SIGGRAPH 96, 313–324. Google ScholarDigital Library
16. Lanthier, M., Maheshwari, A., and Sack, J.-R. 1997. Approximating weighted shortest paths on polyhedral surfaces. In Proc. 13th Annu. ACM Symp. Comput. Geom. 274–283. Google ScholarDigital Library
17. Lee, H., Kim, L., Meyer, M., and Desbrun, M. 2001. Meshes on fire. In Eurographics Workshop on Comp. Animation and Simulation, 75–84. Google ScholarDigital Library
18. Loop, C. T. 1987. Smooth subdivision surfaces based on triangles. Master’s thesis, Mathematics, Univ. of Utah.Google Scholar
19. Martinez, D., Velho, L., and Carvalho, P. C. 2004. Geodesic paths on triangular meshes. In Proc. of SIBGRAPI/SIACG., 210–217. Google ScholarDigital Library
20. Mitchell, J. S. B., Mount, D. M., and Papadimitriou, C. H. 1987. The discrete geodesic problem. SIAM J. of Computing 16(4), 647–668. Google ScholarDigital Library
21. Mitchell, J. 2000. Geometric shortest paths and network optimization. In Handbook of Computational Geometry, J.-R. Sack and J. Urrutia, Eds. Elsevier Science, 633–702.Google Scholar
22. Novotni, M., and Klein, R. 2002. Computing geodesic distances on triangular meshes. In Proc. of WSCG’2002, 341–347.Google Scholar
23. Peyré, G., and Cohen, L. 2003. Geodesic re-meshing and parameterization using front propagation. In Proc. of VLSM’03, 33–40.Google Scholar
24. Peyré, G., and Cohen, L. 2005. Geodesic computations for fast and accurate surface remeshing and parameterization. In Progress in nonlinear differential equations and their applications, vol. 63, 157–171.Google Scholar
25. Pham-Trong, V., Szafran, N., and Biard, L. 2001. Pseudo-geodesics on three-dimensional surfaces and pseudo-geodesic meshes. Numerical Algorithms 26, 305–315.Google ScholarCross Ref
26. Pohl, I. 1971. Bi-directional search. In Machine Intelligence, vol. 6, 124–140.Google Scholar
27. Polthier, K., and Schmies, M. 1998. Straightest geodesics on polyhedral surfaces. Mathematical Visualization. Ed: H. C. Hege, K. Polthier. Springer Verlag, 391–409.Google Scholar
28. Praun, E., Hoppe, H., and Finkelstein. A. 1999. Robust mesh watermarking. In Proc. of SIGGRAPH 99, 49–56. Google ScholarDigital Library
29. Praun, E., Finkelstein, A., and Hoppe, H. 2000. Lapped textures. In Proc. of SIGGRAPH 2000, 465–470. Google ScholarDigital Library
30. Reimers. M. 2004. Topics in Mesh based Modeling. PhD thesis, Mathematics, Univ. of Oslo.Google Scholar
31. Sander, P., Wood, Z., Gortler, S., Snyder, J., and Hoppe, H. 2003. Multi-chart geometry images. In Proc. of Symp. on Geometry Processing, 146–155. Google ScholarDigital Library
32. Sifri, O., Sheffer, A., and Gotsman, C. 2003. Geodesic-based surface remeshing. In Proc. 12th Intnl. Meshing Roundtable, 189–199.Google Scholar
33. Sloan, P.-P. J., Rose, C. F., and Cohen, M. F. 2001. Shape by example. In ACM Symp. on Interactive 3D Graphics, 135–144. Google ScholarDigital Library
34. Zhou, K., Snyder, J., Guo, B., and Shum, H.-Y. 2004. Iso-charts: Stretch-driven mesh parameterization using spectral analysis. In Proc. of the 2004 EG/ACM SIGGRAPH Symp. on Geometry Processing, 45–54. Google ScholarDigital Library
35. Zigelman, G., Kimmel, R., and Kiryati, N. 2002. Texture mapping using surface flattening via multidimensional scaling. IEEE Transactions on Visualization and Computer Graphics 8, 2, 198–207. Google ScholarDigital Library