“Fast and resolution independent line integral convolution” by Stalling and Hege

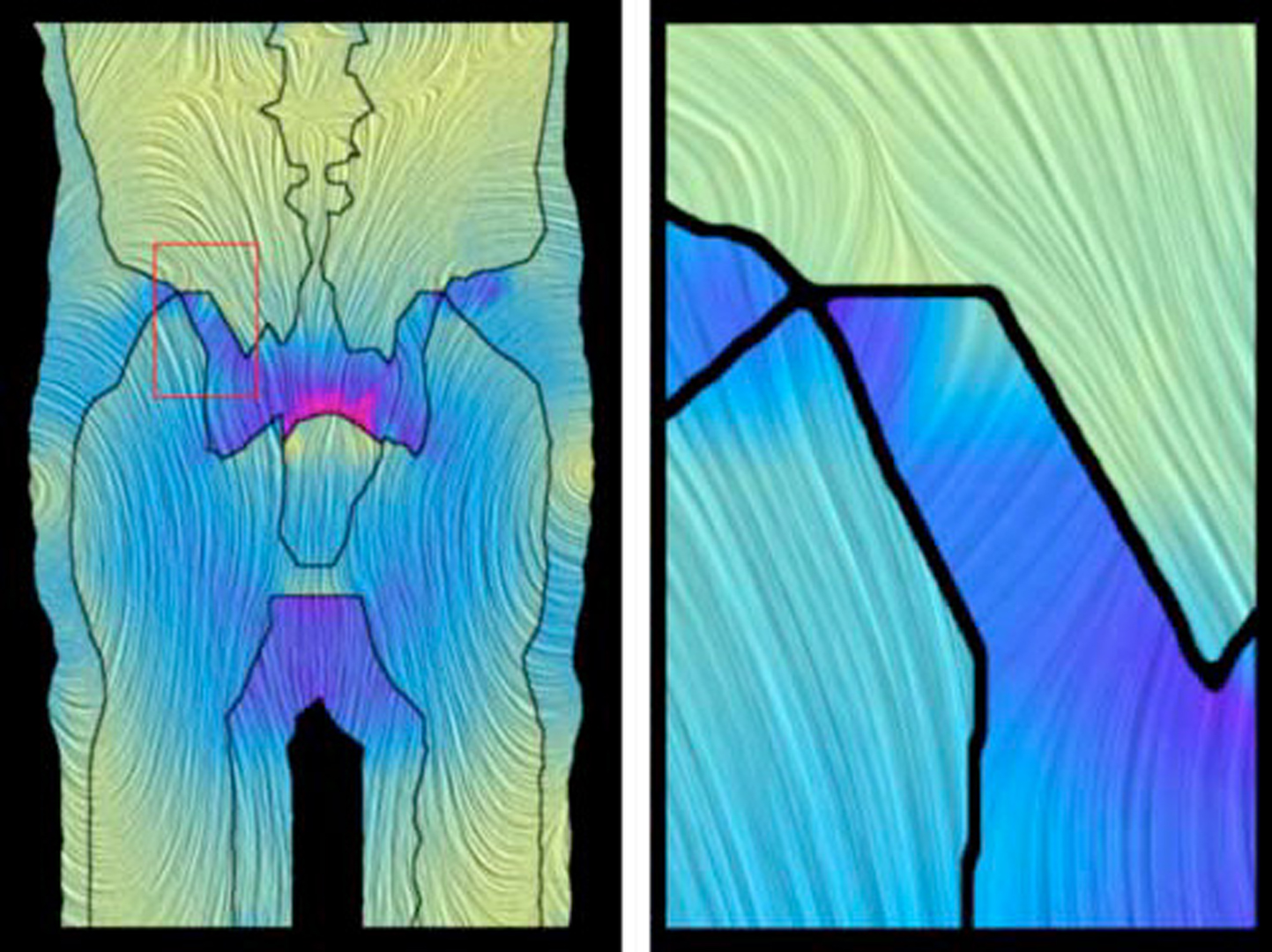
Line Integral Convolution (LIC) is a powerful technique for generating striking images and animations from vector data. Introduced in 1993, the method has rapidly found many application areas, ranging from computer arts to scientific visualization. Based upon locally filtering an input texture along a curved stream line segment in a vector field, it is able to depict directional information at high spatial resolutions. We present a new method for computing LIC images. It employs simple box filter kernels only and minimizes the total number of stream lines to be computed. Thereby it reduces computational costs by an order of magnitude compared to the original algorithm. Our method utilizes fast, error-controlled numerical integrators. Decoupling the characteristic lengths in vector field grid, input texture and output image, it allows computation of filtered images at arbitrary resolution. This feature is of significance in computer animation as well as in scientific visualization, where it can be used to explore vector data by smoothly enlarging structure of details. We also present methods for improved texture animation, again employing box filter kernels only. To obtain an optimal motion effect, spatial decay of correlation between intensities of distant pixels in the output image has to be controlled. This is achieved by blending different phase-shifted box filter animations and by adaptively rescaling the contrast of the output frames.

1. Brian Cabral and Leith (Casey) Leedom. Imaging vector fields using line integral convolution. Proc. of SIGGRAPH ’93 (Anaheim, California, August 1-6,1993). In Computer Graphics 27, Annual Conference Series, 1993, ACM SIGGRAPH, pp. 263-272.
2. J. R. Cash and Alan H. Karp. A variable order Runge-Kutta method for initial value problems with rapidly varying right-hand sides. ACM transactions on Mathematical Software 16, pp. 201-222,1990.
3. Peter Deuflhard and Folkmar Bornemann. Numerische MathematikH: Integration gewghnlicher Differentialgleichungen. Verlag de Gruyter, Berlin, 1994.
4. J.R. Dormand and E J. Prince. Higher order embedded Runge-Kutta formulae. J. Comp. Appl. Math., 7, pp. 67-75, 1981.
5. Lisa K. Forssell. Visualizing flow over curvilinear grid surfaces using line integral convolution. In Proc. of Visualization ’94, (Washington, D.C., Oct. 17-21, 1994), pp. 240-247,IEEE Computer Society, 1994.
6. Paul E. Haeberli. Paint by numbers: Abstract image representations. Proc. of SIGGRAPH ’90 (Dallas, Texas, August 6-10, 1990). In Computer Graphics, 24(4) (August 1991), pp. 207-214.
7. Ernst Hairer, Syvert Paul NOrsett, and Gerhard Wanner. Solving Ordinary Differential Equations I, Nonstiff Problems. Springer Verlag, Berlin, Heidelberg, New York, Tokyo, 1987.
8. James L. Helman and Lambertus Hesselink. Visualizing vector field topology in fluid flows. IEEE Computer Graphics and Applications, 11(3), pp. 36-46, May 1991.
9. Andrea J. S. Hin and Frits H. Post. Visualization of turbulent flow with particles. In Proc. of Visualization ’93 (San Jose, California, October 25-29, 1993), pp. 46-52, IEEE Computer Society, 1993.
10. Jeff E M. Hultquist. Interactive numerical flow visualization using stream Surfaces. Computing Systems in Engineering, 1 (2-4), pp. 349- 353, 1990.
11. Kwan-Liu Ma and Philip J. Smith. Virtual smoke: An interactive 3d flow visualization technique. In Proc. of Visualization ’92 (Boston, MA, October 19-23,1992), pp. 46-52, IEEE Computer Society, 1992.
12. Gordon D. Mallinson. The calculation of the lines of a threedimensional vector field. In Proc. of the International Symposium on Computational Fluid Dynamics (Sydney, Australia, August 1987), pp. 525-534, North-Holland, August 1988.
13. Jerrold E. Marsden and Anthony J. Tromba. Vector Calculus. W.H. Freeman, New York, 3rd edition, 1988.
14. Nelson Max, Barry Becker, and Roger Crawfis. Flow volumes for interactive vector field visualization. In Proc. of Visualization ’93 (San Jose, CA, Oct. 25-29,1993), pp. 19-24, IEEE Computer Society, 1993.
15. Nancy J. Nersessian. Faraday’s field concept. In D. Gooding and E A. J. L. James, eds., Faraday Rediscovered: Essays on the Live and Work of Michael Faraday, pp. 175-187. Stockton Press, New York, 1985.
16. Ken Perlin. An image synthesizer. Proc. of SIGGRAPH ’85 (San Francisco, California, July 22-26, 1985). In Computer Graphics 19, pp. 287-296,1985.
17. William H. Press, Saul A. Teukolsky, William T. Vetterling, and Brian E Flannery. Numerical Recipes in C: The Art of Scientific Computing. Cambridge University Press, Cambridge, 2nd edition, 1992.
18. Jarke J. van Wijk. Spot noise-texture synthesis for data visualization. Proc. of SIGGRAPH ’91 (Las Vegas, Nevada, 28 July – 2 August, 1991). In Computer Graphics, 25, pp. 309-318,1991.
19. Jarke J. van Wijk. Rendering surface-particles. In Proc. of Visualization ’92 (Boston, Massachusetts, October 19-23,1992), pp. 54-61, IEEE Computer Society, 1992.