“Example-based damping design” by Xu and Barbic
Conference:
Type(s):
Title:
- Example-based damping design
Session/Category Title: Clever Solids
Presenter(s)/Author(s):
Moderator(s):
Abstract:
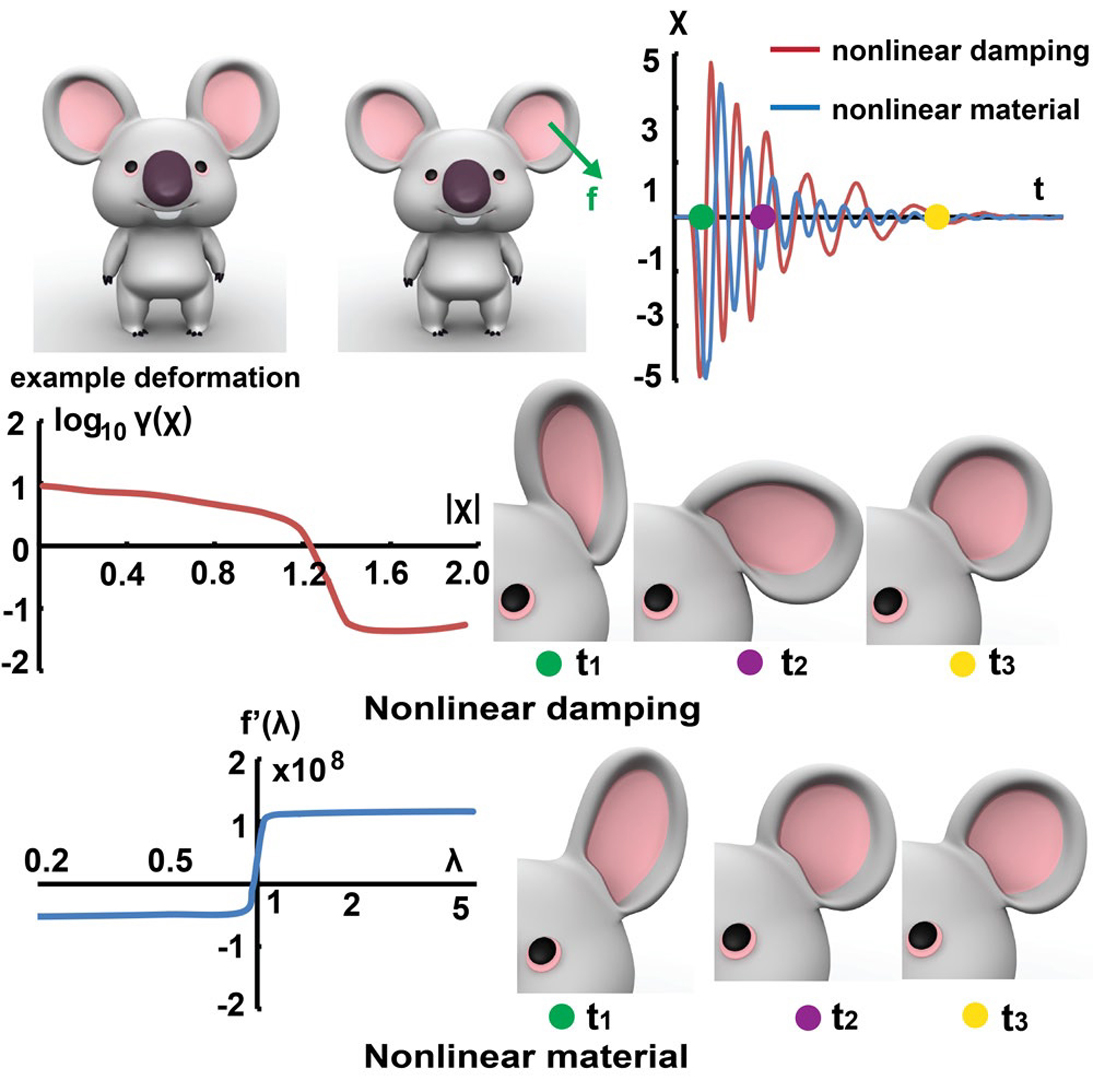
To date, material modeling in physically based computer animation has largely focused on mass and stiffness material properties. However, deformation dynamics is largely affected also by the damping properties. In this paper, we propose an interactive design method for nonlinear isotropic and anisotropic damping of complex three-dimensional solids simulated using the Finite Element Method (FEM). We first give a damping design method and interface whereby the user can set the damping properties so that motion aligned with each of a few chosen example deformations is damped by an independently prescribed amount, whereas the rest of the deformation space follows standard Rayleigh damping, or any viscous damping. Next, we demonstrate how to design nonlinear damping that depends on the magnitude of the deformation along each example deformation, by editing a single spline curve for each example deformation. Our user interface enables an art-directed and intuitive approach to controlling damping in solid simulations. We mathematically prove that our nonlinear anisotropic damping generalizes the frequency-dependent Caughey damping model, when starting from the Rayleigh damping. Finally, we give an inverse design method whereby the damping curve parameters can be inferred automatically from high-level user input, such as the amount of amplitude loss in one oscillation cycle along each of the chosen example deformations. To minimize numerical damping for implicit integration, we introduce an accurate and stable implicit integrator, which removes spurious high-frequency oscillations while only introducing a minimal amount of numerical damping. Our damping can generate effects not possible with previous methods, such as controllable nonlinear decaying envelopes whereby large deformations are damped faster or slower than small deformations, and damping anisotropic effects. We also fit our damping to videos of real-world objects undergoing large deformations, capturing their nonlinear and anisotropic damping dynamics.
References:
1. Sondipon Adhikari. 2001. Damping models for structural vibration. Ph.D. Dissertation. University of Cambridge.Google Scholar
2. David Baraff and Andrew P. Witkin. 1998. Large Steps in Cloth Simulation. In Proc. of ACM SIGGRAPH 98. 43–54. Google ScholarDigital Library
3. Jernej Barbič, Marco da Silva, and Jovan Popović. 2009. Deformable Object Animation Using Reduced Optimal Control. ACM Trans. on Graphics (SIGGRAPH 2009) 28, 3 (2009).Google Scholar
4. Jernej Barbič and Doug L. James. 2005. Real-time subspace integration for St. Venant-Kirchhoff deformable models. ACM Trans. on Graphics (SIGGRAPH 2005) 24, 3 (2005), 982–990.Google Scholar
5. Adam W Bargteil, Chris Wojtan, Jessica K Hodgins, and Greg Turk. 2007. A finite element method for animating large viscoplastic flow. ACM Trans. on Graphics (SIGGRAPH 2007) 26, 3 (2007), 16.Google Scholar
6. Klaus-Jürgen Bathe. 2007. Conserving energy and momentum in nonlinear dynamics: a simple implicit time integration scheme. Computers & structures 85, 7 (2007), 437–445. Google ScholarDigital Library
7. Markus Becker and Matthias Teschner. 2007. Robust and efficient estimation of elasticity parameters using the linear Finite Element Method. In Simulation und Visualisierung Conf. (SimVis). 15–28.Google Scholar
8. Kiran S Bhat, Christopher D Twigg, Jessica K Hodgins, Pradeep K Khosla, Zoran Popović, and Steven M Seitz. 2003. Estimating cloth simulation parameters from video. In Symp. on Computer Animation (SCA). 37–51.Google Scholar
9. B. Bickel, M. Baecher, M. Otaduy, W. Matusik, H. Pfister, and M. Gross. 2009. Capture and Modeling of Non-Linear Heterogeneous Soft Tissue. ACM Trans. on Graphics (SIGGRAPH 2009) 28, 3 (2009), 89:1–89:9.Google Scholar
10. TK Caughey. 1960. Classical normal modes in damped linear dynamic systems. Journal of Applied Mechanics 27, 2 (1960), 269–271. Google ScholarCross Ref
11. TK Caughey and MEJ O’Kelly. 1965. Classical normal modes in damped linear dynamic systems. Journal of Applied Mechanics 32, 3 (1965), 583–588. Google ScholarCross Ref
12. Clarence W De Silva. 2007. Vibration damping, control, and design. CRC Press.Google Scholar
13. Gilles Debunne, Mathieu Desbrun, Marie-Paule Cani, and Alan H. Barr. 2001. Dynamic Real-Time Deformations Using Space & Time Adaptive Sampling. In Proc. of ACM SIGGRAPH 2001. 31–36. Google ScholarDigital Library
14. SJ Elliott, M Ghandchi Tehrani, and RS Langley. 2015. Nonlinear damping and quasi-linear modelling. Phil. Trans. R. Soc. A 373, 2051 (2015), 20140402.Google ScholarCross Ref
15. E Hairer, SP Nørsett, and G Wanner. 1993. Solving ordinary differential equations I: nonstiff problems, vol. 8. Springer (1993).Google Scholar
16. G. Irving, J. Teran, and R. Fedkiw. 2004. Invertible Finite Elements for Robust Simulation of Large Deformation. In Symp. on Computer Animation (SCA). 131–140. Google ScholarDigital Library
17. Ben Jones, Nils Thuerey, Tamar Shinar, and Adam W Bargteil. 2016. Example-based plastic deformation of rigid bodies. ACM Trans. on Graphics (TOG) 35, 4 (2016), 34.Google ScholarDigital Library
18. C. Kane, J. E. Marsden, M. Ortiz, and M. West. 2000. Variational integrators and the Newmark algorithm for conservative and dissipative mechanical systems. Internat. J. Numer. Methods Engrg. 49, 10 (2000), 1295–1325. Google ScholarCross Ref
19. Timothy Lahey. 2002. Modelling hysteresis in the bending of fabrics. (2002).Google Scholar
20. Siwang Li, Jin Huang, Fernando de Goes, Xiaogang Jin, Hujun Bao, and Mathieu Desbrun. 2014. Space-time editing of elastic motion through material optimizationand reduction. ACM Trans. on Graphics (SIGGRAPH 2014) 33, 4 (2014), 108:1–108:10.Google Scholar
21. Yijing Li and Jernej Barbič. 2014. Stable Orthotropic Materials. In Symp. on Computer Animation (SCA). 41–46.Google Scholar
22. Yijing Li, Hongyi Xu, and Jernej Barbic. 2016. Enriching Triangle Mesh Animations With Physically Based Simulation. IEEE Transactions on Visualization and Computer Graphics (2016).Google Scholar
23. D Brandon Lloyd, Nikunj Raghuvanshi, and Naga K Govindaraju. 2011. Sound synthesis for impact sounds in video games. In Symp. on Interactive 3D Graphics and Games.Google ScholarDigital Library
24. J. E. Marsden and M. West. 2001. Discrete Mechanics and Variational Integrators. Acta Numerica 10 (2001), 357–514. Google ScholarCross Ref
25. Sebastian Martin, Bernhard Thomaszewski, Eitan Grinspun, and Markus Gross. 2011. Example-based elastic materials. ACM Trans. on Graphics (SIGGRAPH 2011) 30, 4 (2011), 72.Google Scholar
26. Antoine McNamara, Adrien Treuille, Zoran Popović, and Jos Stam. 2004. Fluid control using the adjoint method. ACM Trans. on Graphics (SIGGRAPH 2004) 23, 3 (2004), 449–456.Google Scholar
27. Eder Miguel, David Miraut, and Miguel A. Otaduy. 2016. Modeling and Estimation of Energy-Based Hyperelastic Objects. Computer Graphics Forum 35, 2 (2016), 385–396. Google ScholarDigital Library
28. Eder Miguel, Rasmus Tamstorf, Derek Bradley, Sara C Schvartzman, Bernhard Thomaszewski, Bernd Bickel, Wojciech Matusik, Steve Marschner, and Miguel A Otaduy. 2013. Modeling and estimation of internal friction in cloth. ACM Transactions on Graphics (SIGGRAPH Asia 2013) 32, 6 (2013), 212.Google Scholar
29. M. Müller and M. Gross. 2004. Interactive Virtual Materials. In Proc. of Graphics Interface 2004. 239–246.Google ScholarDigital Library
30. James O’Brien, Adam Bargteil, and Jessica Hodgins. 2002. Graphical modeling and animation of ductile fracture. ACM Trans. on Graphics (SIGGRAPH 2002) 21, 3 (2002), 291–294.Google Scholar
31. J.F. O’Brien and J.K. Hodgins. 1999. Graphical Modeling and Animation of Brittle Fracture. In Proc. of ACM SIGGRAPH 1999. 111–120. Google ScholarDigital Library
32. Dinesh K. Pai, Kees van den Doel, Doug L. James, Jochen Lang, John E. Lloyd, Joshua L. Richmond, and Som H. Yau. 2001. Scanning Physical Interaction Behavior of 3D Objects. In Proc. of ACM SIGGRAPH 2001. 87–96. Google ScholarDigital Library
33. John William Strutt Baron Rayleigh. 1896. The theory of sound. Vol. 2. Macmillan.Google Scholar
34. Zhimin Ren, Hengchin Yeh, and Ming C Lin. 2013. Example-guided physically based modal sound synthesis. ACM Transactions on Graphics (TOG) 32, 1 (2013), 1.Google ScholarDigital Library
35. Christian Schumacher, Bernhard Thomaszewski, Stelian Coros, Sebastian Martin, Robert Sumner, and Markus Gross. 2012. Efficient simulation of example-based materials. In Symp. on Computer Animation (SCA). 1–8.Google Scholar
36. Auston Sterling and Ming C Lin. 2016. Interactive modal sound synthesis using generalized proportional damping. In Symp. on Interactive 3D Graphics and Games.Google ScholarDigital Library
37. Robert W Sumner and Jovan Popović. 2004. Deformation transfer for triangle meshes. ACM Trans. on Graphics (SIGGRAPH 2004) 23, 3 (2004), 399–405.Google Scholar
38. Joseph Teran, Eftychios Sifakis, Geoffrey Irving, and Ronald Fedkiw. 2005. Robust Quasistatic Finite Elements and Flesh Simulation. In Symp. on Computer Animation (SCA). 181–190. Google ScholarDigital Library
39. Demetri Terzopoulos, John Platt, Alan Barr, and Kurt Fleischer. 1987. Elastically Deformable Models. Computer Graphics (Proc. of ACM SIGGRAPH 87) 21(4) (1987), 205–214.Google Scholar
40. Bin Wang, Longhua Wu, KangKang Yin, Uri Ascher, Libin Liu, and Hui Huang. 2015. Deformation capture and modeling of soft objects. ACM Trans. on Graphics (SIGGRAPH 2015) 34, 4 (2015), 94.Google Scholar
41. Huamin Wang, Florian Hecht, Ravi Ramamoorthi, and James F O’Brien. 2010. Example-based wrinkle synthesis for clothing animation. ACM Trans. on Graphics (SIGGRAPH 2010) 29, 4 (2010), 107.Google Scholar
42. Li-Yi Wei, Sylvain Lefebvre, Vivek Kwatra, and Greg Turk. 2009. State of the art in example-based texture synthesis. In Eurographics 2009, State of the Art Report, EG-STAR. Eurographics Association, 93–117.Google Scholar
43. Robert W Williams. 2010. Measuring and modeling the anisotropic, nonlinear and hysteretic behavior of woven fabrics. Ph.D. Dissertation. University of Iowa.Google Scholar
44. Max Woodbury. 1950. Inverting modified matrices. Memorandum report 42 (1950), 106.Google Scholar
45. J Woodhouse. 1998. Linear damping models for structural vibration. Journal of Sound and Vibration 215, 3 (1998), 547–569. Google ScholarCross Ref
46. Peter Wriggers. 2002. Computational Contact Mechanics. John Wiley & Sons, Ltd.Google Scholar
47. Hongyi Xu and Jernej Barbič. 2016. Pose-space subspace dynamics. ACM Trans. on Graphics (SIGGRAPH 2016) 35, 4 (2016), 35.Google Scholar
48. Hongyi Xu, Yijing Li, Yong Chen, and Jernej Barbič. 2015a. Interactive material design using model reduction. ACM Trans. on Graphics (TOG) 34, 2 (2015), 18.Google ScholarDigital Library
49. Hongyi Xu, Funshing Sin, Yufeng Zhu, and Jernej Barbič. 2015b. Nonlinear material design using principal stretches. ACM Trans. on Graphics (SIGGRAPH 2015) 34, 4 (2015), 75.Google Scholar