“Estimation of yarn-level simulation models for production fabrics” by Sperl, Sánchez-Banderas, Li, Wojtan and Otaduy

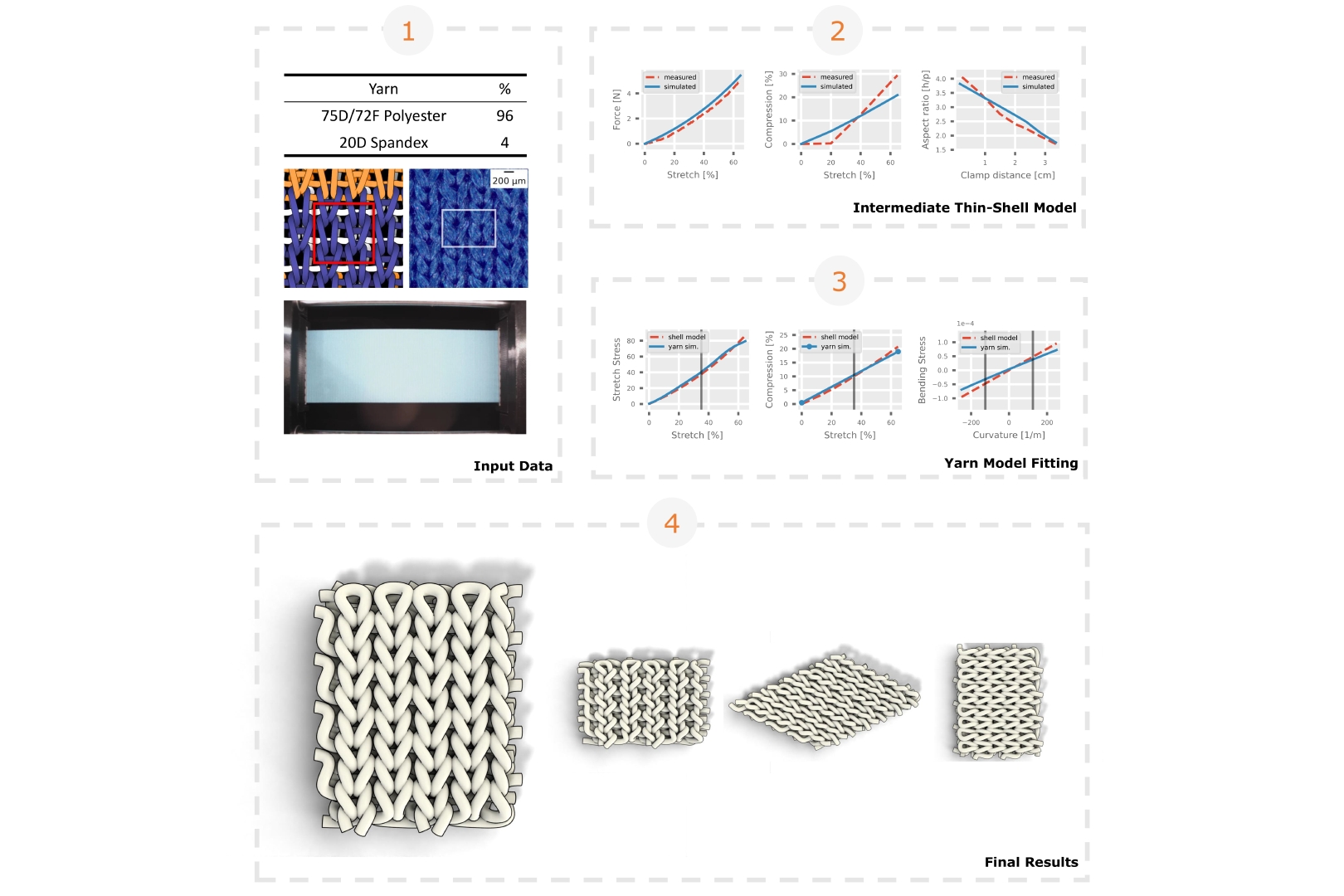
This paper introduces a methodology for inverse-modeling of yarn-level mechanics of cloth, based on the mechanical response of fabrics in the real world. We compiled a database from physical tests of several different knitted fabrics used in the textile industry. These data span different types of complex knit patterns, yarn compositions, and fabric finishes, and the results demonstrate diverse physical properties like stiffness, nonlinearity, and anisotropy.We then develop a system for approximating these mechanical responses with yarn-level cloth simulation. To do so, we introduce an efficient pipeline for converting between fabric-level data and yarn-level simulation, including a novel swatch-level approximation for speeding up computation, and some small-but-necessary extensions to yarn-level models used in computer graphics. The dataset used for this paper can be found at http://mslab.es/projects/YarnLevelFabrics.

1. Miklós Bergou, Basile Audoly, Etienne Vouga, Max Wardetzky, and Eitan Grinspun. 2010. Discrete Viscous Threads. ACM Trans. Graph. 29, 4, Article 116 (2010), 116:1–116:10 pages.Google ScholarDigital Library
2. Miklós Bergou, Max Wardetzky, Stephen Robinson, Basile Audoly, and Eitan Grinspun. 2008. Discrete Elastic Rods. ACM Transactions on Graphics (SIGGRAPH) 27, 3 (2008), 63:1–63:12.Google ScholarDigital Library
3. Kiran S. Bhat, Christopher D. Twigg, Jessica K. Hodgins, Pradeep K. Khosla, Zoran Popović, and Steven M. Seitz. 2003. Estimating Cloth Simulation Parameters from Video. In Proceedings of the 2003 ACM SIGGRAPH/Eurographics Symposium on Computer Animation (San Diego, California) (SCA ’03). Eurographics Association, Goslar, DEU, 37–51.Google Scholar
4. Javier Bonet and Richard D. Wood. 2008. Nonlinear Continuum Mechanics for Finite Element Analysis (2 ed.). Cambridge University Press.Google Scholar
5. Mohammad Reza Bonyadi and Zbigniew Michalewicz. 2017. Particle swarm optimization for single objective continuous space problems: a review. Evolutionary computation 25, 1 (2017), 1–54.Google ScholarDigital Library
6. Katherine L. Bouman, Bei Xiao, Peter Battaglia, and William T. Freeman. 2013. Estimating the Material Properties of Fabric from Video. In Proceedings of the IEEE International Conference on Computer Vision (ICCV).Google Scholar
7. Juan J. Casafranca, Gabriel Cirio, Alejandro Rodríguez, Eder Miguel, and Miguel A. Otaduy. 2020. Mixing Yarns and Triangles in Cloth Simulation. Computer Graphics Forum 39, 2 (2020).Google Scholar
8. Gabriel Cirio, Jorge Lopez-Moreno, David Miraut, and Miguel A. Otaduy. 2014. Yarn-Level Simulation of Woven Cloth. ACM Trans. on Graphics (Proc. of ACM SIGGRAPH Asia) 33, 6 (2014).Google Scholar
9. G. Cirio, J. Lopez-Moreno, and M. A. Otaduy. 2017. Yarn-Level Cloth Simulation with Sliding Persistent Contacts. IEEE Transactions on Visualization and Computer Graphics 23, 2 (2017), 1152–1162.Google ScholarDigital Library
10. Alexandre Derouet-Jourdan, Florence Bertails-Descoubes, Gilles Daviet, and Joëlle Thollot. 2013. Inverse dynamic hair modeling with frictional contact. ACM Transactions on Graphics (TOG) 32, 6 (2013), 1–10.Google ScholarDigital Library
11. Alexandre Derouet-Jourdan, Florence Bertails-Descoubes, and Joëlle Thollot. 2010. Stable inverse dynamic curves. ACM Transactions on Graphics (TOG) 29, 6 (2010), 1–10.Google ScholarDigital Library
12. Eitan Grinspun, Anil N. Hirani, Mathieu Desbrun, and Peter Schröder. 2003. Discrete Shells. In Proceedings of the 2003 ACM SIGGRAPH/Eurographics Symposium on Computer Animation (San Diego, California) (SCA ’03). Eurographics Association, Goslar, DEU, 62–67.Google Scholar
13. Sunil Hadap. 2006. Oriented strands: dynamics of stiff multi-body system. In Proceedings of the 2006 ACM SIGGRAPH/Eurographics symposium on Computer animation. 91–100.Google Scholar
14. Jonathan M. Kaldor, Doug L. James, and Steve Marschner. 2008. Simulating Knitted Cloth at the Yarn Level. ACM Trans. Graph. 27, 3, Article 65 (2008), 65:1–65:9 pages.Google ScholarDigital Library
15. Jonathan M. Kaldor, Doug L. James, and Steve Marschner. 2010. Efficient Yarn-based Cloth with Adaptive Contact Linearization. ACM Transactions on Graphics 29, 4 (July 2010), 105:1–105:10.Google ScholarDigital Library
16. Levi Kapllani, Chelsea Amanatides, Genevieve Dion, Vadim Shapiro, and David E. Breen. 2021. TopoKnit: A Process-Oriented Representation for Modeling the Topology of Yarns in Weft-Knitted Textiles. Graphical Models 118 (2021), 101114.Google ScholarDigital Library
17. S. Kawabata. 1980. The standardization and analysis of hand evaluation. Textile Machinery Soc. Japan.Google Scholar
18. Jonathan Leaf, Rundong Wu, Eston Schweickart, Doug L. James, and Steve Marschner. 2018. Interactive Design of Periodic Yarn-Level Cloth Patterns. ACM Trans. Graph. 37, 6, Article 202 (2018).Google ScholarDigital Library
19. Minchen Li, Zachary Ferguson, Teseo Schneider, Timothy Langlois, Denis Zorin, Daniele Panozzo, Chenfanfu Jiang, and Danny M. Kaufman. 2020. Incremental Potential Contact: Intersection-and Inversion-Free, Large-Deformation Dynamics. ACM Trans. Graph. 39, 4, Article 49 (jul 2020).Google Scholar
20. Junbang Liang, Ming C. Lin, and Vladlen Koltun. 2019. Differentiable Cloth Simulation for Inverse Problems. In Conference on Neural Information Processing Systems (NeurIPS).Google Scholar
21. D. Liu, S. Koric, and A. Kontsos. 2018. Parallelized Finite Element Analysis of Knitted Textile Mechanical Behavior. Journal of Engineering Materials and Technology 141, 2 (12 2018).Google ScholarCross Ref
22. D. S. Lyle. 1977. Performance of Textiles. John Wiley & Sons, New York.Google Scholar
23. E. Miguel, D. Bradley, B. Thomaszewski, B. Bickel, W. Matusik, M. A. Otaduy, and S. Marschner. 2012. Data-Driven Estimation of Cloth Simulation Models. Comput. Graph. Forum 31, 2pt2 (2012), 519–528.Google Scholar
24. Eder Miguel, Rasmus Tamstorf, Derek Bradley, Sara C. Schvartzman, Bernhard Thomaszewski, Bernd Bickel, Wojciech Matusik, Steve Marschner, and Miguel A. Otaduy. 2013. Modeling and Estimation of Internal Friction in Cloth. ACM Trans. Graph. 32, 6, Article 212 (2013).Google ScholarDigital Library
25. Zahra Montazeri, Chang Xiao, Yun Fei, Changxi Zheng, and Shuang Zhao. 2019. Mechanics-aware modeling of cloth appearance. IEEE transactions on visualization and computer graphics 27, 1 (2019), 137–150.Google ScholarDigital Library
26. Vidya Narayanan, Kui Wu, Cem Yuksel, and James McCann. 2019. Visual Knitting Machine Programming. ACM Trans. Graph. 38, 4, Article 63 (2019).Google ScholarDigital Library
27. W Oberkampf and Christopher Roy. 2010. Verification and Validation in Scientific Computing. Cambridge University Press.Google Scholar
28. F. T. Peirce. 1930. The “Handle” of Cloth as a Measurable Quantity. Journal of the Textile Institute Transactions 21, 9 (1930), T377–T416.Google ScholarCross Ref
29. Jesús Pérez, Miguel A Otaduy, and Bernhard Thomaszewski. 2017. Computational design and automated fabrication of kirchhoff-plateau surfaces. ACM Transactions on Graphics (TOG) 36, 4 (2017), 1–12.Google ScholarDigital Library
30. Jesús Pérez, Bernhard Thomaszewski, Stelian Coros, Bernd Bickel, José A Canabal, Robert Sumner, and Miguel A Otaduy. 2015. Design and fabrication of flexible rod meshes. ACM Transactions on Graphics (TOG) 34, 4 (2015), 1–12.Google ScholarDigital Library
31. Michael JD Powell. 1994a. A direct search optimization method that models the objective and constraint functions by linear interpolation. In Advances in optimization and numerical analysis. Springer, 51–67.Google Scholar
32. M. J. D. Powell. 1994b. A Direct Search Optimization Method That Models the Objective and Constraint Functions by Linear Interpolation. Springer Netherlands, Dordrecht, 51–67.Google Scholar
33. Abdullah Haroon Rasheed, Victor Romero, Florence Bertails-Descoubes, Stefanie Wuhrer, Jean-Sebastien Franco, and Arnaud Lazarus. 2020. Learning to Measure the Static Friction Coefficient in Cloth Contact. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR).Google Scholar
34. Yannick Remion, Jean-Michel Nourrit, and Didier Gillard. 1999. Dynamic Animation Of Spline Like Objects. In Proc. of WSCG.Google Scholar
35. Victor Romero, Mickaël Ly, Abdullah Haroon Rasheed, Raphaël Charrondière, Arnaud Lazarus, Sébastien Neukirch, and Florence Bertails-Descoubes. 2021. Physical Validation of Simulators in Computer Graphics: A New Framework Dedicated to Slender Elastic Structures and Frictional Contact. ACM Trans. Graph. 40, 4, Article 66 (2021).Google ScholarDigital Library
36. Tom F. H. Runia, Kirill Gavrilyuk, Cees G. M. Snoek, and Arnold W. M. Smeulders. 2020. Cloth in the Wind: A Case Study of Physical Measurement Through Simulation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR).Google Scholar
37. Christian Schumacher, Steve Marschner, Markus Gross, and Bernhard Thomaszewski. 2018. Mechanical Characterization of Structured Sheet Materials. ACM Trans. Graph. 37, 4, Article 148 (2018).Google ScholarDigital Library
38. Breannan Smith, Fernando De Goes, and Theodore Kim. 2018. Stable Neo-Hookean Flesh Simulation. ACM Trans. Graph. 37, 2, Article 12 (2018).Google ScholarDigital Library
39. Georg Sperl, Rahul Narain, and Chris Wojtan. 2020. Homogenized Yarn-Level Cloth. ACM Transactions on Graphics (TOG) 39, 4 (2020).Google ScholarDigital Library
40. Georg Sperl, Rahul Narain, and Chris Wojtan. 2021. Mechanics-Aware Deformation of Yarn Pattern Geometry. ACM Transactions on Graphics (TOG) 40, 4 (2021).Google ScholarDigital Library
41. Rosa M. Sánchez-Banderas, Alejandro Rodríguez, Héctor Barreiro, and Miguel A. Otaduy. 2020. Robust Eulerian-on-Lagrangian Rods. ACM Trans. Graph. 39, 4, Article 59 (2020).Google ScholarDigital Library
42. Pascal Volino, Nadia Magnenat-Thalmann, and Francois Faure. 2009. A Simple Approach to Nonlinear Tensile Stiffness for Accurate Cloth Simulation. ACM Trans. Graph. 28, 4, Article 105 (2009).Google ScholarDigital Library
43. Paras Wadekar, Vignesh Perumal, Genevieve Dion, Antonios Kontsos, and David Breen. 2020. An optimized yarn-level geometric model for Finite Element Analysis of weft-knitted fabrics. Computer Aided Geometric Design 80 (2020), 101883.Google ScholarCross Ref
44. Huamin Wang, James F. O’Brien, and Ravi Ramamoorthi. 2011. Data-Driven Elastic Models for Cloth: Modeling and Measurement. In ACM SIGGRAPH 2011 Papers (Vancouver, British Columbia, Canada) (SIGGRAPH ’11). Association for Computing Machinery, New York, NY, USA, Article 71.Google ScholarDigital Library
45. X. Wang, X. Liu, and C. Hurren Deakin. 2008. Physical and mechanical testing of textiles. In Fabric Testing, Jinlian Hu (Ed.). Woodhead Publishing, 90–124.Google Scholar
46. Max Wardetzky, Miklós Bergou, David Harmon, Denis Zorin, and Eitan Grinspun. 2007. Discrete Quadratic Curvature Energies. Comput. Aided Geom. Des. 24, 8–9 (2007), 499–518.Google ScholarDigital Library
47. Kui Wu, Hannah Swan, and Cem Yuksel. 2019. Knittable Stitch Meshes. ACM Trans. Graph. 38, 1, Article 10 (2019).Google ScholarDigital Library
48. Rundong Wu, Joy Xiaoji Zhang, Jonathan Leaf, Xinru Hua, Ante Qu, Claire Harvey, Emily Holtzman, Joy Ko, Brooks Hagan, Doug James, François Guimbretière, and Steve Marschner. 2020. Weavecraft: An Interactive Design and Simulation Tool for 3D Weaving. ACM Trans. Graph. 39, 6, Article 210 (2020).Google ScholarDigital Library
49. Shan Yang, Junbang Liang, and Ming C. Lin. 2017. Learning-Based Cloth Material Recovery From Video. In Proceedings of the IEEE International Conference on Computer Vision (ICCV).Google Scholar
50. Cem Yuksel, Jonathan M. Kaldor, Doug L. James, and Steve Marschner. 2012. Stitch Meshes for Modeling Knitted Clothing with Yarn-level Detail. ACM Trans. Graph. 31, 4 (2012), 37:1–37:12.Google ScholarDigital Library
51. Jonas Zehnder, Stelian Coros, and Bernhard Thomaszewski. 2016. Designing structurally-sound ornamental curve networks. ACM Transactions on Graphics (TOG) 35, 4 (2016), 1–10.Google ScholarDigital Library