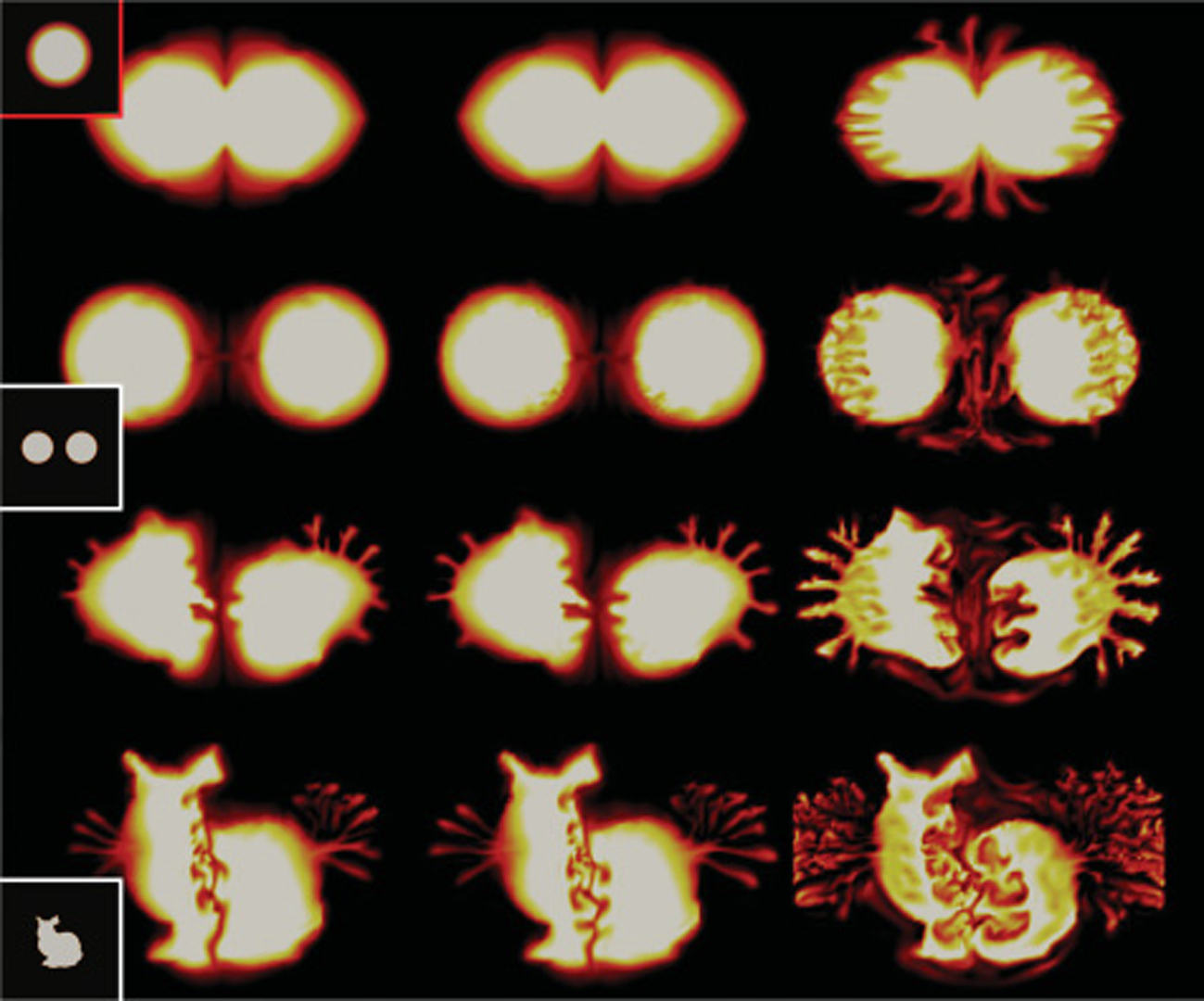
“Efficient Solver for Spacetime Control of Smoke” by Manocha and Pan
Conference:
Type(s):
Title:
- Efficient Solver for Spacetime Control of Smoke
Session/Category Title: Fluid Control & Synthesis
Presenter(s)/Author(s):
Abstract:
We present a novel algorithm to control the physically-based animation of smoke. Given a set of keyframe smoke shapes, we compute a dense sequence of control force fields that can drive the smoke shape to match several keyframes at certain time instances. Our approach formulates this control problem as a spacetime optimization constrained by partial differential equations. In order to compute the locally optimal control forces, we alternatively optimize the velocity fields and density fields using an alternating direction method of multiplier (ADMM) optimizer. In order to reduce the high complexity of multiple passes of fluid resimulation during velocity field optimization, we utilize the coherence between consecutive fluid simulation passes. We demonstrate the benefits of our approach by computing accurate solutions on 2D and 3D benchmarks. In practice, we observe up to an order of magnitude improvement over prior optimal control methods.
References:
1. Edward H. Adelson, Charles H. Anderson, James R. Bergen, Peter J. Burt, and Joan M. Ogden. 1984. Pyramid methods in image processing. RCA Engineer 29, 6 (1984), 33–41.Google Scholar
2. Alexis Angelidis, Fabrice Neyret, Karan Singh, and Derek Nowrouzezahrai. 2006. A controllable, fast and stable basis for vortex based smoke simulation. In Proceedings of the 2006 ACM SIGGRAPH/Eurographics Symposium on Computer Animation (SCA’06). Eurographics Association, 25–32. Google ScholarDigital Library
3. Hans Georg Bock and Karl-Josef Plitt. 1984. A multiple shooting algorithm for direct solution of optimal control problems. In Proceedings of the IFAC World Congress.Google ScholarCross Ref
4. Alfio Borzi and R. Griesse. 2005. Experiences with a space–time multigrid method for the optimal control of a chemical turbulence model. International Journal for Numerical Methods in Fluids 47, 8–9 (2005), 879–885.Google ScholarCross Ref
5. Stephen Boyd, Neal Parikh, Eric Chu, Borja Peleato, and Jonathan Eckstein. 2011. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Foundations and Trends® in Machine Learning 3, 1 (2011), 1–122. Google ScholarDigital Library
6. Achi Brandt and Oren E. Livne. 2011. Multigrid Techniques: 1984 Guide With Applications to Fluid Dynamics. Vol. 67. SIAM.Google Scholar
7. Richard H. Byrd, Peihuang Lu, Jorge Nocedal, and Ciyou Zhu. 1995. A limited memory algorithm for bound constrained optimization. SIAM Journal on Scientific Computing 16, 5 (1995), 1190–1208. Google ScholarDigital Library
8. Nuttapong Chentanez, Bryan E. Feldman, François Labelle, James F. O’Brien, and Jonathan R. Shewchuk. 2007. Liquid simulation on lattice-based tetrahedral meshes. In Proceedings of the 2007 ACM SIGGRAPH/Eurographics Symposium on Computer Animation. Eurographics Association, 219–228. Google ScholarDigital Library
9. Nuttapong Chentanez and Matthias Müller. 2011. Real-time eulerian water simulation using a restricted tall cell grid. In ACM Transactions on Graphics (TOG), Vol. 30. ACM, 82. Google ScholarDigital Library
10. Raanan Fattal and Dani Lischinski. 2004. Target-Driven Smoke Animation. In ACM Transactions on Graphics (TOG), Vol. 23. ACM, 441–448. Google ScholarDigital Library
11. Ronald Fedkiw, Jos Stam, and Henrik Wann Jensen. 2001. Visual simulation of smoke. In Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques. ACM, 15–22. Google ScholarDigital Library
12. James Gregson, Ivo Ihrke, Nils Thuerey, and Wolfgang Heidrich. 2014. From capture to simulation: Connecting forward and inverse problems in fluids. ACM Trans. Graph. 33, 4, Article 139 (July 2014), 11 pages. Google ScholarDigital Library
13. F. H. Harlow and J. E. Welch. 1965. Numerical calculation of time-dependent viscous incompressible flow of fluid with free surfaces. Physics of Fluids 8 (1965), 2182–2188.Google ScholarCross Ref
14. Roland Herzog and Karl Kunisch. 2010. Algorithms for PDE-constrained optimization. GAMM-Mitteilungen 33, 2 (2010), 163–176.Google ScholarCross Ref
15. Michael Hinze, Michael Köster, and Stefan Turek. 2012. A space-time multigrid method for optimal flow control. In Constrained Optimization and Optimal Control for Partial Differential Equations. Springer, 147–170.Google Scholar
16. Michael Lentine, Matthew Cong, Saket Patkar, and Ronald Fedkiw. 2012. Simulating free surface flow with very large time steps. In Proceedings of the ACM SIGGRAPH/Eurographics Symposium on Computer Animation (SCA’12). Eurographics Association, Aire-la-Ville, Switzerland, 107–116. http://dl.acm.org/citation.cfm?id=2422356.2422373. Google ScholarDigital Library
17. Brian P. Leonard. 1979. A stable and accurate convective modelling procedure based on quadratic upstream interpolation. Computer Methods in Applied Mechanics and Engineering 19, 1 (1979), 59–98. Google ScholarDigital Library
18. David Q. Mayne and Hannah Michalska. 1990. Receding horizon control of nonlinear systems. Automatic Control, IEEE Transactions on 35, 7 (1990), 814–824.Google ScholarCross Ref
19. Antoine McNamara, Adrien Treuille, Zoran Popović, and Jos Stam. 2004. Fluid control using the adjoint method. In ACM Transactions On Graphics (TOG), Vol. 23. ACM, 449–456. Google ScholarDigital Library
20. Igor Mordatch, Emanuel Todorov, and Zoran Popović. 2012. Discovery of complex behaviors through contact-invariant optimization. ACM Transactions on Graphics (TOG) 31, 4 (2012), 43. Google ScholarDigital Library
21. Rahul Narain, Matthew Overby, and George E. Brown. 2016. ADMM ⊇ rojective dynamics: Fast simulation of general constitutive models. In Proceedings of the ACM SIGGRAPH/Eurographics Symposium on Computer Animation (SCA’16). Eurographics Association, Aire-la-Ville, Switzerland, 21–28. http://dl.acm.org/citation.cfm?id=2982818.2982822. Google ScholarDigital Library
22. Michael B. Nielsen and Robert Bridson. 2011. Guide shapes for high resolution naturalistic liquid simulation. In ACM Transactions on Graphics (TOG), Vol. 30. ACM, 83. Google ScholarDigital Library
23. Michael B. Nielsen and Brian B. Christensen. 2010. Improved Variational Guiding of Smoke Animations. In Computer Graphics Forum, Vol. 29. Wiley Online Library, 705–712.Google Scholar
24. Jorge Nocedal and Stephen Wright. 2006. Numerical Optimization. Springer Science 8 Business Media.Google Scholar
25. Zherong Pan, Jin Huang, Yiying Tong, Changxi Zheng, and Hujun Bao. 2013. Interactive localized liquid motion editing. ACM Transactions on Graphics (TOG) 32, 6 (2013), 184. Google ScholarDigital Library
26. Dmitry Pavlov, Patrick Mullen, Yiying Tong, Eva Kanso, Jerrold E. Marsden, and Mathieu Desbrun. 2011. Structure-preserving discretization of incompressible fluids. Physica D: Nonlinear Phenomena 240, 6 (2011), 443–458.Google ScholarCross Ref
27. Nick Rasmussen, Doug Enright, Duc Nguyen, Sebastian Marino, Nigel Sumner, Willi Geiger, Samir Hoon, and Ron Fedkiw. 2004. Directable photorealistic liquids. In Proceedings of the 2004 ACM SIGGRAPH/Eurographics Symposium on Computer Animation. Eurographics Association, 193–202. Google ScholarDigital Library
28. Karthik Raveendran, Nils Thuerey, Chris Wojtan, and Greg Turk. 2012. Controlling liquids using meshes. In Proceedings of the ACM SIGGRAPH/Eurographics Symposium on Computer Animation. Eurographics Association, 255–264. Google ScholarDigital Library
29. Karthik Raveendran, Chris Wojtan, Nils Thuerey, and Greg Turk. 2014. Blending liquids. ACM Transactions on Graphics (TOG) 33, 4 (2014), 137. Google ScholarDigital Library
30. Lin Shi and Yizhou Yu. 2005. Taming liquids for rapidly changing targets. In Proceedings of the 2005 ACM SIGGRAPH/Eurographics Symposium on Computer Animation. ACM, 229–236. Google ScholarDigital Library
31. Adrien Treuille, Antoine McNamara, Zoran Popović, and Jos Stam. 2003. Keyframe control of smoke simulations. ACM Transactions on Graphics (TOG) 22 (2003), 716–723. Google ScholarDigital Library
32. S. P. Vanka. 1983. Fully Coupled Calculation of Fluid Flows with Limited Use of Computer Storage. Technical Report. Argonne National Lab., IL.Google Scholar
33. Xinxin Zhang and Robert Bridson. 2014. A PPPM fast summation method for fluids and beyond. ACM Transactions on Graphics (TOG) 33, 6 (2014), 206. Google ScholarDigital Library
34. Yongning Zhu and Robert Bridson. 2005. Animating sand as a fluid. In ACM Transactions on Graphics (TOG), Vol. 24. ACM, 965–972. Google ScholarDigital Library