“Editing the topology of 3D models by sketching” by Ju, Zhou and Hu

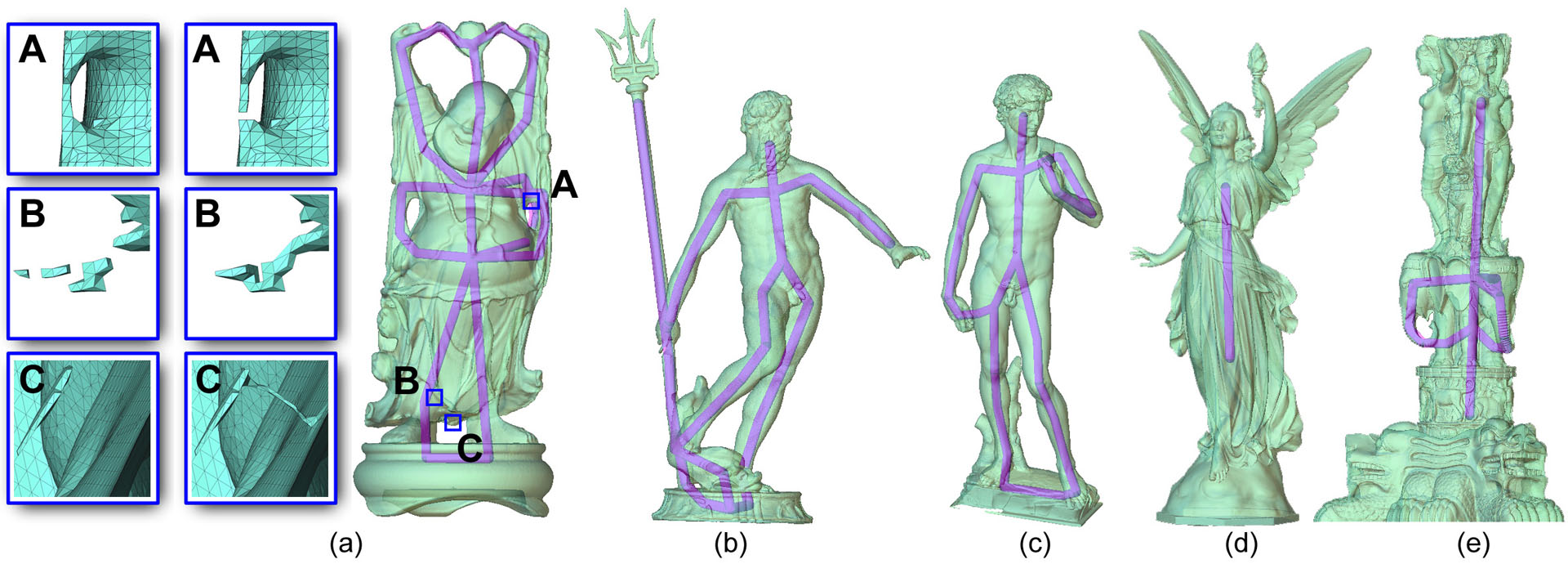
We present a method for modifying the topology of a 3D model with user control. The heart of our method is a guided topology editing algorithm. Given a source model and a user-provided target shape, the algorithm modifies the source so that the resulting model is topologically consistent with the target. Our algorithm permits removing or adding various topological features (e.g., handles, cavities and islands) in a common framework and ensures that each topological change is made by minimal modification to the source model. To create the target shape, we have also designed a convenient 2D sketching interface for drawing 3D line skeletons. As demonstrated in a suite of examples, the use of sketching allows more accurate removal of topological artifacts than previous methods, and enables creative designs with specific topological goals.

1. Aktouf, Z., Bertrand, G., and Perroton, L. 1996. A 3d-hole closing algorithm. In 6th International Workshop on Discrete Geometry for Computer Imagery, 36–47. Google ScholarDigital Library
2. Andujar, C., Brunet, P., and Ayala, D. 2002. Topology-reducing surface simplification using a discrete solid representation. ACM Trans. Graph. 21, 2, 88–105. Google ScholarDigital Library
3. Bischoff, S., and Kobbelt, L. 2002. Isosurface reconstruction with topology control. In Pacific Conference on Computer Graphics and Applications, 246–255. Google ScholarDigital Library
4. Bischoff, S., Pavic, D., and Kobbelt, L. 2005. Automatic restoration of polygon models. ACM Trans. Graph. 24, 4, 1332–1352. Google ScholarDigital Library
5. Davis, J., Agrawala, M., Chuang, E., Popovi;, Z., and Salesin, D. 2003. A sketching interface for articulated figure animation. In SCA ’03: Proceedings of the 2003 ACM SIG-GRAPH/Eurographics symposium on Computer animation, Eurographics Association, Aire-la-Ville, Switzerland, Switzerland, 320–328. Google ScholarDigital Library
6. Diefenbach, P. J. 1996. Pipeline rendering: interaction and realism through hardware-based multi-pass rendering. PhD thesis, Philadelphia, PA, USA. Google ScholarDigital Library
7. El-Sana, J., and Varshney, A. 1997. Controlled simplification of genus for polygonal models. In IEEE Visualization, 403–412. Google ScholarDigital Library
8. Guskov, I., and Wood, Z. J. 2001. Topological noise removal. In Graphics Interface, 19–26. Google ScholarDigital Library
9. Han, X., Xu, C., Braga-Neto, U., and Prince, J. L. 2002. Topology correction in brain cortex segmentation using a multi-scale, graph-based algorithm. IEEE Trans. Med. Imaging 21, 2, 109–121.Google ScholarCross Ref
10. Hatcher, A. 2002. Algebraic Topology. Cambridge University Pres.Google Scholar
11. Igarashi, T., Matsuoka, S., and Tanaka, H. 1999. Teddy: A sketching interface for 3d freeform design. In SIGGRAPH, 409–416. Google ScholarDigital Library
12. Ju, T., Losasso, F., Schaefer, S., and Warren, J. 2002. Dual contouring of hermite data. In SIGGRAPH ’02: Proceedings of the 29th annual conference on Computer graphics and interactive techniques, ACM Press, New York, NY, USA, 339–346. Google ScholarDigital Library
13. Ju, T. 2004. Robust repair of polygonal models. ACM Trans. Graph. 23, 3, 888–895. Google ScholarDigital Library
14. Kho, Y, and Garland, M. 2005. Sketching mesh deformations. In SI3D, 147–154. Google ScholarDigital Library
15. Kriegeskorte, N., and Goebel, R. 2001. An efficient algorithm for topologically correct segmentation of the cortical sheet in anatomical mr volumes. Neuroimage 14, 2 (August), 329–346.Google ScholarCross Ref
16. Mammen, A. 1989. Transparency and antialiasing algorithms implemented with the virtual pixel maps technique. IEEE Comput. Graph. Appl. 9, 4, 43–55. Google ScholarDigital Library
17. Mangin, J.-F., Frouin, V., Bloch, I., Regis, J., and Lopez-Krahe, J. 1995. From 3d magnetic resonance images to structural representations of the cortex topography using topology preserving deformations. Journal of Mathematical Imaging and Vision 5, 297–318. Google ScholarDigital Library
18. Matveev, S. 2003. Algorithmic Topology and Classification of 3-Manifolds. Springer-Verlag Berlin. Google ScholarDigital Library
19. Nealen, A., Sorkine, O., Alexa, M., and Cohen-Or, D. 2005. A sketch-based interface for detail-preserving mesh editing. ACM Trans. Graph. 24, 3, 1142–1147. Google ScholarDigital Library
20. Nooruddin, F. S., and Turk, G. 2003. Simplification and repair of polygonal models using volumetric techniques. IEEE Trans. Vis. Comput. Graph. 9, 2, 191–205. Google ScholarDigital Library
21. Sharf, A., Lewiner, T., Shamir, A., Kobbelt, L., and Cohen-Or, D. 2006. Competing fronts for coarse-to-fine surface reconstruction. In Eurographics, 389–398.Google Scholar
22. Shattuck, D. W., and Leahy, R. M. 2001. Automated graph based analysis and correction of cortical volume topology. IEEE Trans. Med. Imaging 20, 11, 1167–1177.Google ScholarCross Ref
23. Szymczak, A., and Vanderhyde, J. 2003. Extraction of topologically simple isosurfaces from volume datasets. In IEEE Visualization, 67–74. Google ScholarDigital Library
24. Wood, Z. J., Hoope, H., Desbrun, M., and Schröder, P. 2004. Removing excess topology from isosurfaces. ACM Trans. Graph. 23, 2, 190–208. Google ScholarDigital Library
25. Zhou, Q.-Y., Ju, T., and Hu, S.-M. 2007. Topology repair of solid models using skeletons. IEEE Transactions on Visualization and Computer Graphics, to appear. Google ScholarDigital Library