“Discrete multiscale vector field decomposition” by Tong, Lombeyda, Hirani and Desbrun

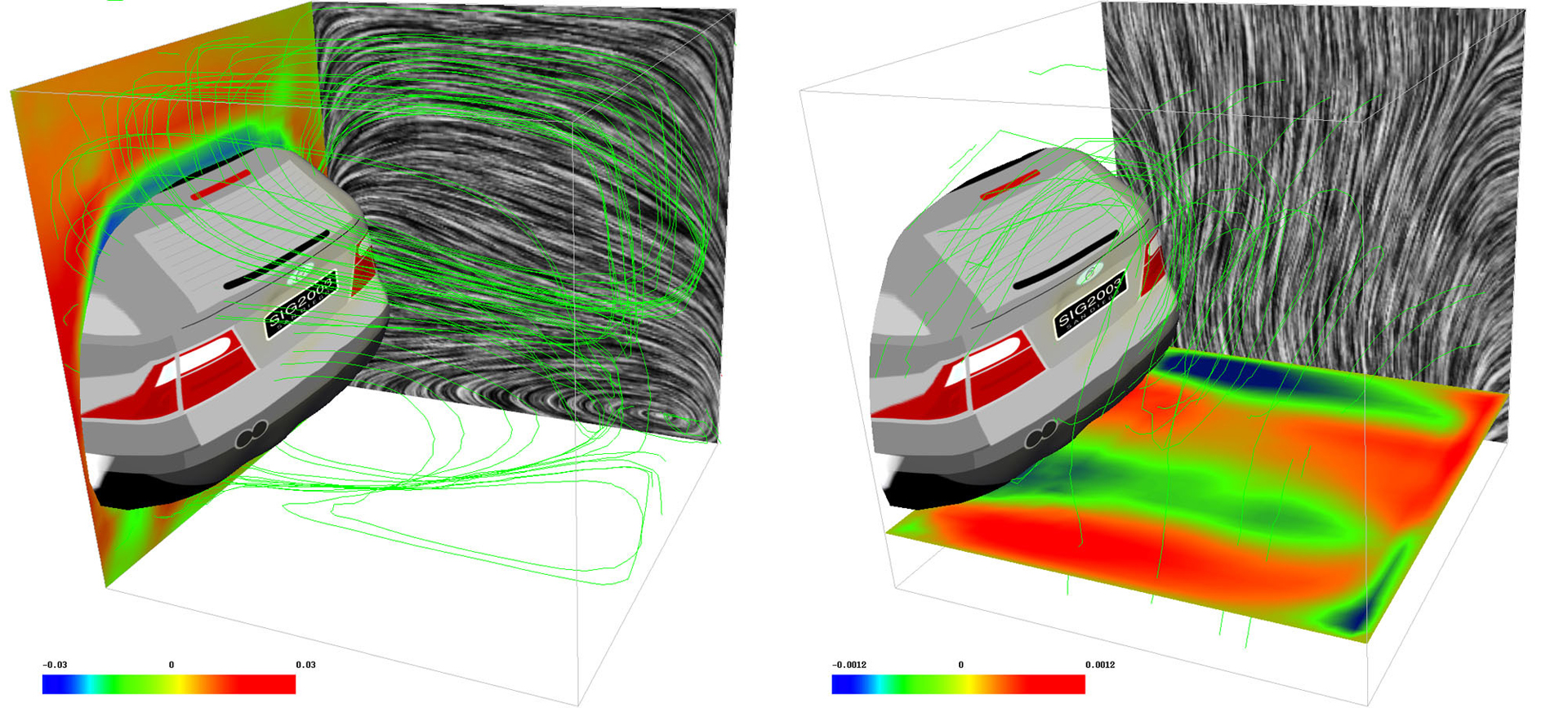
While 2D and 3D vector fields are ubiquitous in computational sciences, their use in graphics is often limited to regular grids, where computations are easily handled through finite-difference methods. In this paper, we propose a set of simple and accurate tools for the analysis of 3D discrete vector fields on arbitrary tetrahedral grids. We introduce a variational, multiscale decomposition of vector fields into three intuitive components: a divergence-free part, a curl-free part, and a harmonic part. We show how our discrete approach matches its well-known smooth analog, called the Helmotz-Hodge decomposition, and that the resulting computational tools have very intuitive geometric interpretation. We demonstrate the versatility of these tools in a series of applications, ranging from data visualization to fluid and deformable object simulation.

1. ABRAHAM, R., MARSDEN, J., AND RATIU, T., Eds. Manifolds, Tensor Analysis, and Applications. Applied Mathematical Sciences Vol. 75, Springer, 1988. Google ScholarDigital Library
2. ABRAHAM, R., AND SHAW, C., Eds. Dynamics: The Geometry of Behavior. Ariel Press (Santa Cruz, CA), 1984.Google Scholar
3. AMROUCHE, C., BERNARDI, C., DAUGE, M., AND GIRAULT, V. Vector Potentials in Three-Dimensional Non-smooth Domains. Math. Meth. Appl. Sci. 21 (1998), pp.823–864.Google Scholar
4. BAUER, D., AND PEIKERT, R. Vortex Tracking in Scale-Space. Symposium on Visualization (Joint Eurographics-IEEE TVCG) (2002). Google ScholarDigital Library
5. CABRAL, B., AND LEEDOM, L. C. Imaging Vector Fields Using Line Integral Convolution. In Proceedings of SIGGRAPH (1993), pp.263–272. Google Scholar
6. DEBUNNE, G., DESBRUN, M., CANI, M.-P., AND BARR, A. H. Dynamic Real-Time Deformations Using Space & Time Adaptive Sampling. In Proceedings of ACM SIGGRAPH (August 2001), pp. 31–36. Google Scholar
7. DESBRUN, M., MEYER, M., SCHRÖDER, P., AND BARR, A. H. Implicit Fairing of Arbitrary Meshes using Diffusion and Curvature Flow. In Proceedings of ACM SIGGRAPH (1999), pp.317–324. Google Scholar
8. DESBRUN, M., MEYER, M., SCHRÖDER, P., AND BARR, A. H. Anisotropic Feature-Preserving Denoising of Height Fields and Bivariate Data. In Graphics Interface (2000), pp. 145–152.Google Scholar
9. DIEWALD, U., PREUER, T., AND RUMPF, M. Anisotropic Diffusion in Vector Field Visualization on Euclidean Domains and Surfaces. In IEEE Trans. on Vis. and Computer Graphics (2000), pp. 139–149. Google ScholarDigital Library
10. FEDKIW, R., STAM, J., AND JENSEN, H. W. Visual Simulation of Smoke. In Proceedings of ACM SIGGRAPH (2001), pp. 23–30. Google Scholar
11. GLOBUS, A., LEVIT, C., AND LASINSKI, T. A Tool for Visualizing the Topology of Three-Dimensional Vector Fields. In Proceedings of IEEE Visualization (1991), pp. 33–40. Google ScholarDigital Library
12. GUSKOV, I., SWELDENS, W., AND SCHRÖDER, P. Multiresolution Signal Processing for Meshes. In Proceedings of ACM SIGGRAPH (August 1999), pp. 325–334. Google Scholar
13. HIRANI, A. N. Discrete Exterior Calculus. PhD thesis, Caltech, 2003. Google ScholarDigital Library
14. LEEUW, W. C. D., AND LIERE, R. V. Collapsing Flow Topology using Area Metrics. In Proceedings of Visualization (1999), pp. 349–354. Google ScholarDigital Library
15. LINDEBERG, T. Scale-Space Theory: A Basic Tool for Analysing Structures at Different Scales. Journal of Applied Statistics 21, 2 (1994), pp. 225–270.Google ScholarCross Ref
16. MANN, S., AND ROCKWOOD, A. Computing Singularities of 3D Vector Fields with Geometric Algebra. In Proceedings of IEEE Visualization (2002), pp. 283–289. Google ScholarDigital Library
17. MCCORMICK, S. F. Multilevel Adaptive Methods for Partial Differential Equations — Chapter 2: The Finite Volume Method, vol. 6. SIAM, 1989.Google Scholar
18. MEYER, M., DESBRUN, M., SCHRÖDER, P., AND BARR, A. H. Discrete Differential-Geometry Operators for Triangulated 2-Manifolds. In Proceedings of VisMath (2002).Google Scholar
19. PERONA, P., AND MALIK, J. Scale-space and Edge Detection using Anisotropic Diffusion. IEEE Transactions on Pattern Analysis and Machine Intelligence 12, 7 (1990), pp. 629–639. Google ScholarDigital Library
20. PINKALL, U., AND POLTHIER, K. Computing Discrete Minimal Surfaces. Experimental Mathematics 2, 1 (1993), pp. 15–36.Google Scholar
21. POLTHIER, K. Computational Aspects of Discrete Minimal Surfaces. Proceedings of the Clay Summer School on Global Theory of Minimal Surfaces (Hass, Hoffman, Jaffe, Rosenberg, Schoen, and Wolf Editors) (2002).Google Scholar
22. POLTHIER, K., AND PREUSS, E. Variational Approach to Vector Field Decomposition. Scientific Visualization, Springer Verlag (Proc. of Eurographics Workshop on Scientific Visualization) (2000).Google Scholar
23. POLTHIER, K., AND PREUSS, E. Identifying Vector Fields Singularities using a Discrete Hodge Decomposition. Visualization and Mathematics III, Eds: H. C. Hege, K. Polthier, Springer Verlag (2002).Google Scholar
24. PREUER, T., AND RUMPF, M. Anisotropic Nonlinear Diffusion in Flow Visualization. In Proceedings of Visualization (1999), pp. 325–332. Google ScholarDigital Library
25. STAM, J. Stable fluids. In Proceedings of ACM SIGGRAPH (1999), pp. 121–128. Google ScholarDigital Library
26. TAUBIN, G. Linear Anisotropic Mesh Filtering. Tech. Rep. IBM Reserach Report RC2213, 2001.Google Scholar
27. TRICOCHE, X., SCHEUERMANN, G., AND HAGEN, H. A Topology Simplification Method for 2D Vector Fields. In Proceedings of IEEE Visualization (2000), pp. 359–366. Google ScholarDigital Library
28. VAN WIJK, J. J. Image-based Flow Visualization. In Proceedings of ACM SIGGRAPH (2002), pp. 745–754. Google Scholar
29. WESTERMANN, R., JOHNSON, C., AND ERTL, T. A Level-set Method for Visualization. In Proceedings of Visualization (2000), pp. 147–154. Google ScholarDigital Library