“Discrete Beta-splines” by Joe

  • ©

Conference:


Type(s):


Title:

    Discrete Beta-splines

Presenter(s)/Author(s):


Abstract:


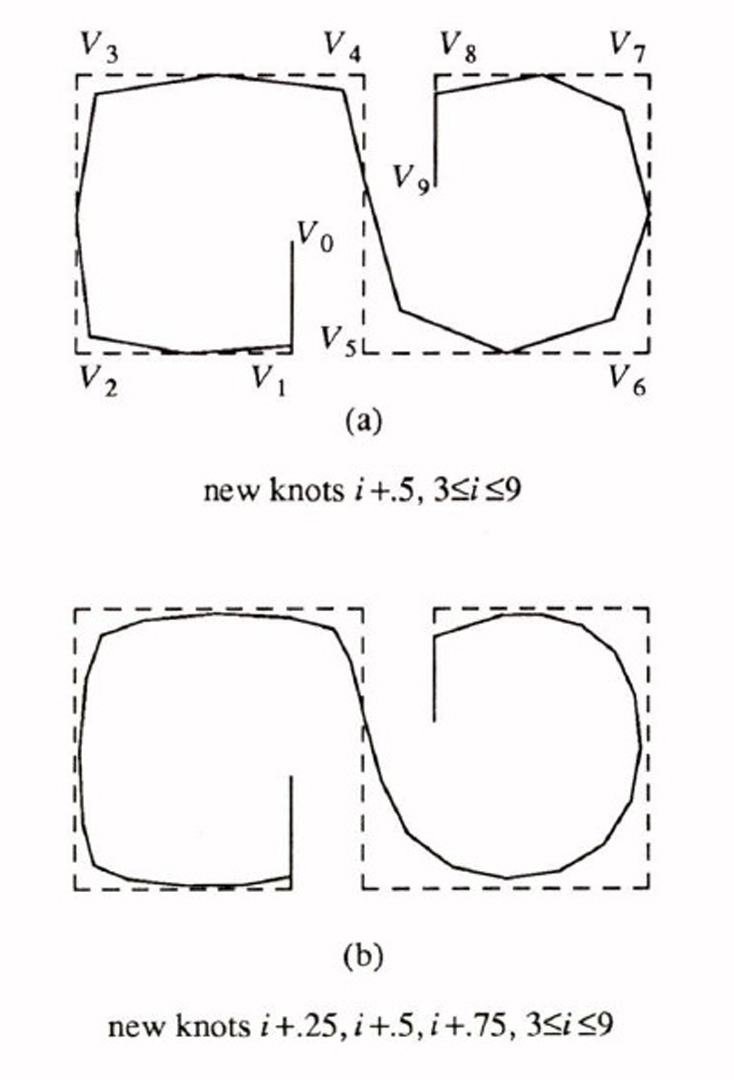
    Goodman (1985) and Joe (1986) have given explicit formulas for (cubic) Beta-splines on uniform knot sequences with varying ß1 and ß2 values at the knots, and nonuniform knot sequences with varying ß2 values at the knots, respectively. The advantage of the latter formula is that it can also be used for knot sequences with multiple knots. Discrete Beta-splines arise when a Beta-spline curve is subdivided, i.e. the knot sequence is refined so that the curve is expressed in terms of a larger number of control vertices and Beta-splines. We prove that discrete Beta-splines satisfy the same properties as discrete B-splines, and present an algorithm for computing discrete Beta-splines and the new control vertices using the explicit formula of Joe (1986).

References:


    1. B. A. Barsky (1981), The Beta-sptine: a local representation based on shape parameters and fundamental geometric measures, Ph.D. Dissertation, Dept. of CompUter Science, Univ. of Utah.]] 
    2. B. A. Barsky and J. C. Beatty (1983), Local control of bias and tension in Beta-splines, ACM Transactions on Graphics, 2, pp. 109-134.]] 
    3. B. A. Barsky (1986), Computer Graphics and Geometric Modelling Using Beta-splines, Springer-Verlag, Tokyo.]] 
    4. R. H. Barrels and J. C. Beatty (1984), Beta-splines with a difference, Technical Report CS-83-40, Dept. of Computer Science, Univ. of Waterloo.]]
    5. R. H. Bartels, J. C. Beatty, and B. A. Barsky (1987), An Introduction to the Use of Splines in Computer Graphics, to be published by Morgan Kaufman Publishers, Los Altos, Califor- Ilia.]] 
    6. W. Boehm (1980), Inserting new knots into B-spline curves, Computer-AidedDesign, 12, pp. 199-201.]]
    7. W. Boehm and H. Prautzsch (1985), The insertion algorithm, Computer-AidedDesign, 17, pp. 58-59.]]
    8. W. Boehm (1985), Curvature continuous curves and surface~, Computer Aided Geometric Design, 2, pp. 313-323.]]
    9. E. Cohen, T. Lyche, and R. Riesenfeld (1980), Discrete B-splines and subdivision techniques in computer-aided geometric design and computer graphics, Computer Graphics and Image Processing, 14, pp. 87-111.]]
    10. G. Farin (1982), Visually C 2 cubic splines, Computer-Aided Design, 14, pp. 137-139.]]
    11. G. Farin (1985), Some remarks on V2-splines, Computer Aided Geometric Design, 2, pp. 325-328.]] 
    12. T. N. T. Goodman (1985), Properties of Beta-splines, J. Approximation Theory, 44, pp. 132-153.]]
    13. T. N. T. Goodman and K. Unsworth (1985), Generation of Betaspline curves using a recurrence relation, in Fundamental Algorithms for Computer Graphics, Springer-Vedag, Berlin, pp. 325-357.]]
    14. T. N. T. Goodman and K. Unsworth (1986), Manipulating shape and producing geometric continuity in Beta-spline curves, IEEE Computer Graphics and Applications, 6, No. 2, pp. 50-56.]]
    15. B. Joe (1986), An explicit formula for nonuniform Beta-splines, Technical Report TR86-21, Dept. of Computing Science, Univ. of Alberta.]]
    16. B. Joe (1987), Rational Beta-spline curves and surfaces and discrete Beta-splines, Technical Report TR87-04, Dept. of Computing Science, Univ. of Alberta.]]
    17. T. Lyche and K. Morken (1986), Making the Oslo algorithm more efficient, SIAM J. Numer. Anal., 23, pp. 663-675.]] 
    18. H. Prautzsch (1984), A short proof of the Oslo algorithm, Computer Aided Geometric Design, 1, pp. 95-96.]]
    19. H. Prautzsch (1985), Letter to the editor, Computer Aided Geometric Design, 2, p. 329.]]
    20. G. W. Stewart (1973), Introduction to Matrix Computations, Academic Press, New York.]]

ACM Digital Library Publication:


Overview Page: