“Discovery of complex behaviors through contact-invariant optimization” by Mordatch, Todorov and Popovic

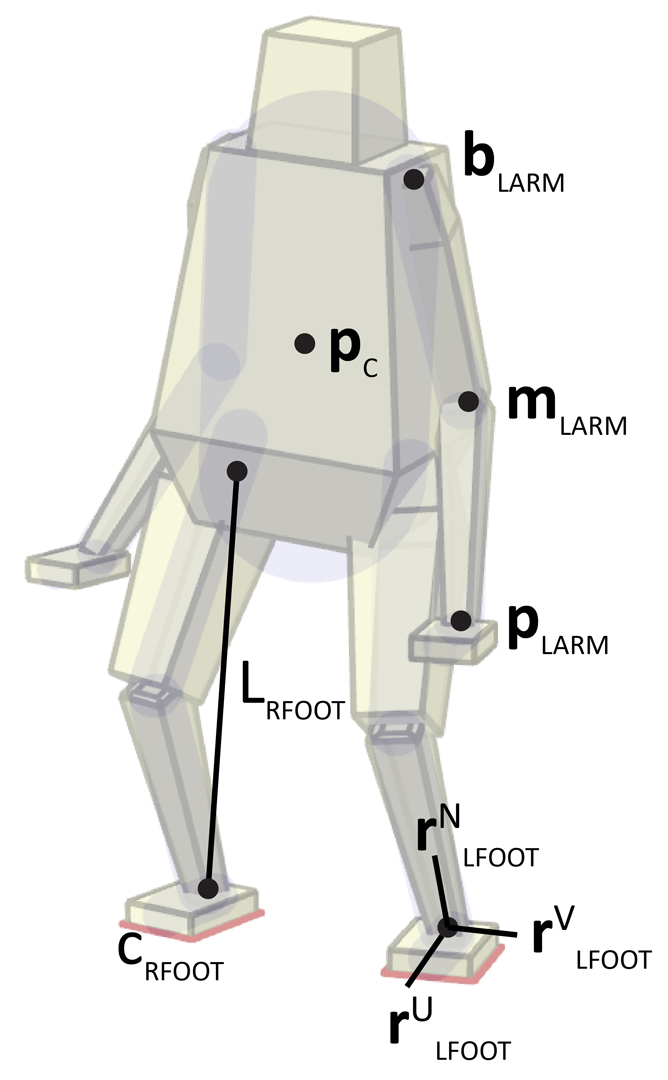
We present a motion synthesis framework capable of producing a wide variety of important human behaviors that have rarely been studied, including getting up from the ground, crawling, climbing, moving heavy objects, acrobatics (hand-stands in particular), and various cooperative actions involving two characters and their manipulation of the environment. Our framework is not specific to humans, but applies to characters of arbitrary morphology and limb configuration. The approach is fully automatic and does not require domain knowledge specific to each behavior. It also does not require pre-existing examples or motion capture data.At the core of our framework is the contact-invariant optimization (CIO) method we introduce here. It enables simultaneous optimization of contact and behavior. This is done by augmenting the search space with scalar variables that indicate whether a potential contact should be active in a given phase of the movement. These auxiliary variables affect not only the cost function but also the dynamics (by enabling and disabling contact forces), and are optimized together with the movement trajectory. Additional innovations include a continuation scheme allowing helper forces at the potential contacts rather than the torso, as well as a feature-based model of physics which is particularly well-suited to the CIO framework. We expect that CIO can also be used with a full physics model, but leave that extension for future work.

1. Bouyarmane, K., and Kheddar, A. 2011. Multi-contact stances planning for multiple agents. In ICRA, 5246–5253.Google Scholar
2. Brubaker, M. A., Sigal, L., and Fleet, D. J. 2009. Estimating contact dynamics. In ICCV, 2389–2396.Google Scholar
3. Chestnutt, J. 2007. Navigation Planning for Legged Robots. PhD thesis, Carnegie Mellon University.Google Scholar
4. Chi Wu, J., and Popovic, Z. 2010. Terrain-adaptive bipedal locomotion control. ACM Trans. Graph. 29, 4. Google ScholarDigital Library
5. Coros, S., Beaudoin, P., and van de Panne, M. 2009. Robust task-based control policies for physics-based characters. ACM Trans. Graph. 28, 5. Google ScholarDigital Library
6. Coros, S., Karpathy, A., Jones, B., Revéret, L., and van de Panne, M. 2011. Locomotion skills for simulated quadrupeds. ACM Trans. Graph. 30, 4, 59. Google ScholarDigital Library
7. da Silva, M., Durand, F., and Popovic, J. 2009. Linear bellman combination for control of character animation. ACM Trans. Graph. 28, 3. Google ScholarDigital Library
8. de Lasa, M., Mordatch, I., and Hertzmann, A. 2010. Feature-Based Locomotion Controllers. ACM Trans. Graphics 29, 3. Google ScholarDigital Library
9. Erez, T., Tassa, Y., and Todorov, E. 2011. Infinite-horizon model predictive control for periodic tasks with contacts. In Robotics: Science and Systems.Google Scholar
10. Faloutsos, P., van de Panne, M., and Terzopoulos, D. 2001. Composable controllers for physics-based character animation. In SIGGRAPH, 251–260. Google ScholarDigital Library
11. Fang, A. C., and Pollard, N. S. 2003. Efficient synthesis of physically valid human motion. ACM Trans. Graph. 22, 3, 417–426. Google ScholarDigital Library
12. Grassia, F. S. 1998. Practical parameterization of rotations using the exponential map. J. Graph. Tools 3 (March), 29–48. Google ScholarDigital Library
13. Hauser, K. K., Bretl, T., Latombe, J.-C., Harada, K., and Wilcox, B. 2008. Motion planning for legged robots on varied terrain. I. J. Robotic Res. 27, 11–12, 1325–1349.Google ScholarCross Ref
14. Hodgins, J. K., and Pollard, N. S. 1997. Adapting simulated behaviors for new characters. In SIGGRAPH, 153–162. Google ScholarDigital Library
15. Hodgins, J. K., Wooten, W. L., Brogan, D. C., and O’Brien, J. F. 1995. Animating human athletics. In SIGGRAPH, 71–78. Google ScholarDigital Library
16. Jain, S., and Liu, C. K. 2011. Controlling physics-based characters using soft contacts. ACM Trans. Graph. (SIGGRAPH Asia) 30 (Dec.), 163:1–163:10. Google ScholarDigital Library
17. Kajita, S., Matsumoto, O., and Saigo, M. 2001. Real-time 3D walking pattern generation for a biped robot with telescopic legs. In Proc. ICRA, 2299–2306.Google Scholar
18. Kalisiak, M., and van de Panne, M. 2001. A grasp-based motion planning algorithm for character animation. Journal of Visualization and Computer Animation 12, 3, 117–129.Google ScholarCross Ref
19. Kolter, J. Z., Rodgers, M. P., and Ng, A. Y. 2008. A control architecture for quadruped locomotion over rough terrain. In ICRA, 811–818.Google Scholar
20. Kuffner, J. J., Nishiwaki, K., Kagami, S., Inaba, M., and Inoue, H. 2003. Motion planning for humanoid robots. In ISRR, 365–374.Google Scholar
21. Kuo, A. D., Donelan, J. M., and Ruina, A. 2005. Energetic consequences of walking like an inverted pendulum: step-to-step transitions. Exercise and sport sciences reviews 33, 2 (Apr.), 88–97.Google Scholar
22. Lee, S.-H., and Goswami, A. 2010. Ground reaction force control at each foot: A momentum-based humanoid balance controller for non-level and non-stationary ground. In IROS, 3157–3162.Google Scholar
23. Liu, C. K., Hertzmann, A., and Popovic, Z. 2005. Learning physics-based motion style with nonlinear inverse optimization. ACM Trans. Graph. 24, 3, 1071–1081. Google ScholarDigital Library
24. Liu, C. K., Hertzmann, A., and Popovic, Z. 2006. Composition of complex optimal multi-character motions. In Symposium on Computer Animation, 215–222. Google ScholarDigital Library
25. Liu, C. K. 2009. Dextrous manipulation from a grasping pose. ACM Trans. Graph. 28, 3. Google ScholarDigital Library
26. Manchester, I. R., Mettin, U., Iida, F., and Tedrake, R. 2011. Stable dynamic walking over uneven terrain. I. J. Robotic Res. 30, 3, 265–279. Google ScholarDigital Library
27. Mordatch, I., de Lasa, M., and Hertzmann, A. 2010. Robust physics-based locomotion using low-dimensional planning. ACM Trans. Graph. 29, 4. Google ScholarDigital Library
28. Muico, U., Lee, Y., Popović, J., and Popović, Z. 2009. Contact-aware Nonlinear Control of Dynamic Characters. ACM Trans. Graphics 28, 3, 81. Google ScholarDigital Library
29. Muico, U., Popovic, J., and Popovic, Z. 2011. Composite control of physically simulated characters. ACM Trans. Graph. 30, 3, 16. Google ScholarDigital Library
30. Popovic, Z., and Witkin, A. P. 1999. Physically based motion transformation. In SIGGRAPH, 11–20. Google ScholarDigital Library
31. Pratt, J., Carff, J., and Drakunov, S. 2006. Capture point: A step toward humanoid push recovery. In in 6th IEEE-RAS International Conference on Humanoid Robots, 200–207.Google Scholar
32. Safonova, A., Hodgins, J. K., and Pollard, N. S. 2004. Synthesizing physically realistic human motion in low-dimensional, behavior-specific spaces. ACM Trans. Graph. 23, 3, 514–521. Google ScholarDigital Library
33. Seipel, J. E., and Holmes, P. 2005. Running in three dimensions: Analysis of a point-mass sprung-leg model. I. J. Robotic Res. 24, 8, 657–674. Google ScholarDigital Library
34. Srinivasan, M., and Ruina, A. 2005. Computer optimization of a minimal biped model discovers walking and running. Nature (Sept.).Google Scholar
35. Stephens, B. 2011. Push Recovery Control for Force-Controlled Humanoid Robots. PhD thesis, Carnegie Mellon University.Google Scholar
36. Sutton, R., Precup, D., and Singh, S. 1999. Between mdps and semi-mdps: A framework for temporal abstraction in reinforcement learning. Artificial Intelligence 112, 181–211. Google ScholarDigital Library
37. Todorov, E. 2011. A convex, smooth and invertible contact model for trajectory optimization. In ICRA, 1071–1076.Google Scholar
38. Van De Panne, M., and Lamouret, A. 1995. Guided optimization for balanced locomotion. In 6th Eurographics Workshop on Animation and Simulation, Computer Animation and Simulation, September, 1995, Springer, Maastricht, Pays-Bas, D. Terzopoulos and D. Thalmann, Eds., Eurographics, 165–177.Google ScholarCross Ref
39. Vukobratovic, M., and Borovac, B. 2004. Zero-moment point – thirty five years of its life. I. J. Humanoid Robotics 1, 1, 157–173.Google ScholarCross Ref
40. Wampler, K., and Popovic, Z. 2009. Optimal gait and form for animal locomotion. ACM Trans. Graph. 28, 3. Google ScholarDigital Library
41. Wang, J. M., Fleet, D. J., and Hertzmann, A. 2009. Optimizing Walking Controllers. ACM Trans. Graphics 28, 5, 168. Google ScholarDigital Library
42. Witkin, A., and Kass, M. 1988. Spacetime Constraints. In Proc. SIGGRAPH, vol. 22, 159–168. Google ScholarDigital Library
43. Wooten, W. L., and Hodgins, J. K. 2000. Simulating leaping, tumbling, landing, and balancing humans. In ICRA, 656–662.Google Scholar
44. Ye, Y., and Liu, C. K. 2010. Optimal feedback control for character animation using an abstract model. ACM Trans. Graph. 29, 4. Google ScholarDigital Library
45. Yin, K., Loken, K., and Van de Panne, M. 2007. Simbicon: simple biped locomotion control. ACM Trans. Graph. 26, 3, 105. Google ScholarDigital Library
46. Yin, K., Coros, S., Beaudoin, P., and van de Panne, M. 2008. Continuation methods for adapting simulated skills. ACM Trans. Graph. 27, 3. Google ScholarDigital Library