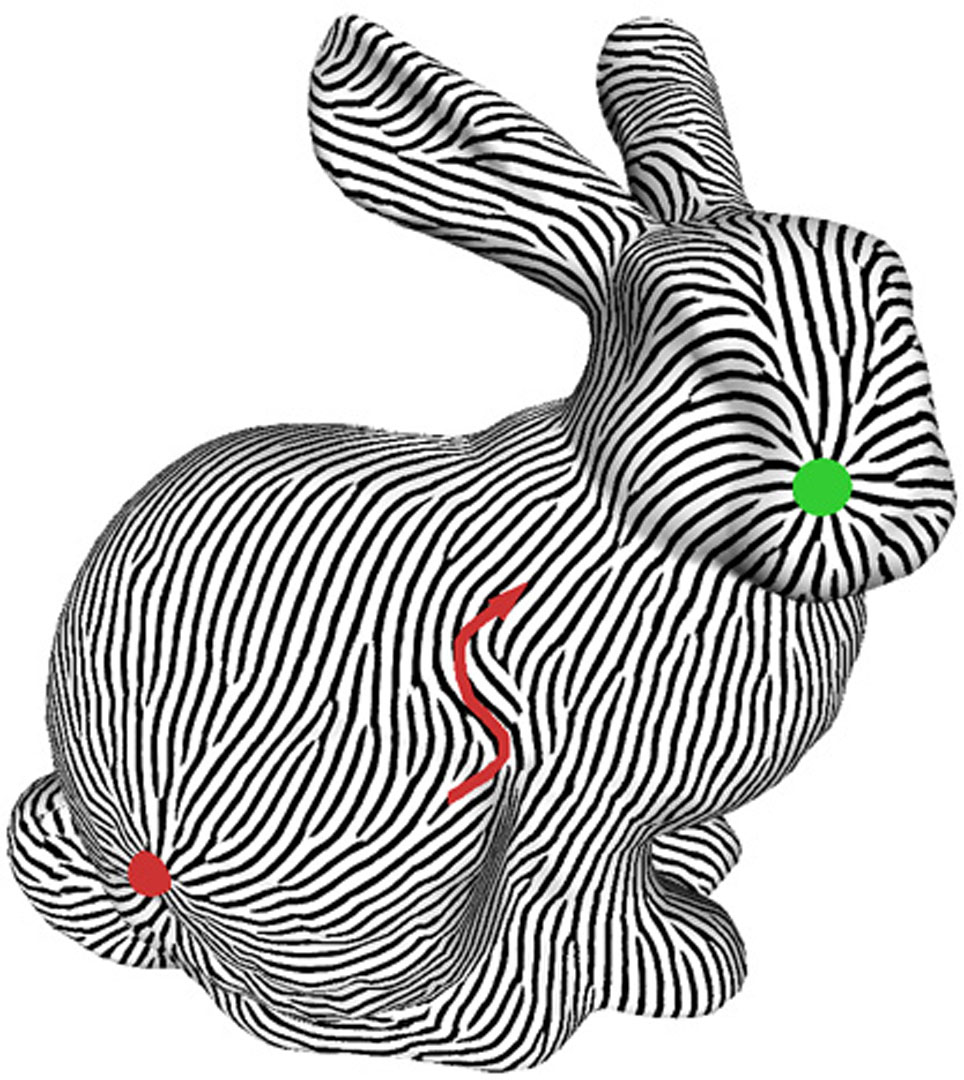
“Design of tangent vector fields” by Fisher, Schröder, Desbrun and Hoppe

Tangent vector fields are an essential ingredient in controlling surface appearance for applications ranging from anisotropic shading to texture synthesis and non-photorealistic rendering. To achieve a desired effect one is typically interested in smoothly varying fields that satisfy a sparse set of user-provided constraints. Using tools from Discrete Exterior Calculus, we present a simple and efficient algorithm for designing such fields over arbitrary triangle meshes. By representing the field as scalars over mesh edges (i.e., discrete 1-forms), we obtain an intrinsic, coordinate-free formulation in which field smoothness is enforced through discrete Laplace operators. Unlike previous methods, such a formulation leads to a linear system whose sparsity permits efficient pre-factorization. Constraints are incorporated through weighted least squares and can be updated rapidly enough to enable interactive design, as we demonstrate in the context of anisotropic texture synthesis.

1. Arnold, D. N., Brezzi, F., Cockburn, B., and Marini, D. 2000. Discontinuous Galerkin Methods for Elliptic Problems. In Discontinuous Galerkin Methods: Theory, Comp. and Appl., vol. 11 of LNCSE. Springer Verlag, 101–89.Google Scholar
2. Arnold, D. N., Falk, R. S., and Winther, R. 2006. Finite Element Exterior Calculus, Homological Techniques, and Applications. Acta Numerica 15, 1–155.Google ScholarCross Ref
3. Bobenko, A. I., and Springborn, B. A. A Discrete Laplace-Beltrami Operator for Simplicial Surfaces. Preprint (2005) http://www.arxiv.org/math/0503219; to appear in Discr. & Comp. Geom. Google ScholarCross Ref
4. Bossavit, A., and Kettunen, L. 1999. Yee-Schemes on a Tetrahedral Mesh, with Diagonal Lumping. Int. J. Num. Model. 12, 129–142.Google ScholarCross Ref
5. Botsch, M., and Kobbelt, L. 2004. An Intuitive Framework for Real-Time Freeform Modeling. ACM Trans. Graph. 23, 3, 630–634. Google ScholarDigital Library
6. Botsch, M., Bommes, D., and Kobbelt, L. 2005. Efficient Linear System Solvers for Mesh Processing. In Mathematics of Surfaces XI, vol. 3604 of LNCS. Springer Verlag, 62–83. Google ScholarDigital Library
7. Cabral, B., and Leedom, L. C. 1993. Imaging Vector Fields Using Line Integral Convolution. In Proc. ACM/SIGGRAPH Conf., 263–270. Google ScholarDigital Library
8. Cook, R. L., and DeRose, T. 2005. Wavelet Noise. ACM Trans. Graph. 24, 3, 803–811. Google ScholarDigital Library
9. Davis, T. A., and Hager, W. M. 1999. Modifying a Sparse Cholesky Factorization. SIAM J. Matr. Anal. Appl. 20, 3, 606–627. Google ScholarDigital Library
10. Davis, T. A., and Hager, W. M. 2001. Multiple-Rank Modifications of a Sparse Cholesky Factorization. SIAM J. Matr. Anal. Appl. 22, 4, 997–1013. Google ScholarDigital Library
11. Desbrun, M., Kanso, E., and Tong, Y. 2006. Discrete Differential Forms for Computational Modeling. In Grainspun et al. {2006}. Google ScholarDigital Library
12. Dodziuk, J., and Patodi, V. K. 1976. Riemannian Structures and Triangulations of Manifolds. J. Ind. Math. Soc. 40, 1–4, 1–52.Google Scholar
13. Elcott, S., and Schröder, P. 2006. Building Your Own DEC at Home. In Grinspun et al. {2006}. Google ScholarDigital Library
14. Elcott, S., Tong, Y., Kanso, E., Schröder, P., and Desbrun, M. 2007. Stable, Circulation-Preserving, Simplicial Fluids. ACM Trans. Graph. 26, 1. Google ScholarDigital Library
15. Fisher, M., Springborn, B., Bobenko, A. I., and Schröder, P. 2006. An Algorithm for the Construction of Intrinsic Delaunay Triangulations with Applications to Digital Geometry Processing. In Grinspun et al. {2006}. Google ScholarDigital Library
16. Gortler, S. J., Gotsman, C., and Thurston, D. 2006. Discrete One-Forms on Meshes and Applications to 3D Mesh Parameterization. Comput. Aided Geom. Des. 33, 2, 83–112. Google ScholarCross Ref
17. Grinspun, E., Schröder, P., and Desbrun, M., Eds. 2006. Discrete Differential Geometry. Course Notes. ACM SIGGRAPH. Google ScholarDigital Library
18. Gu, X., and Yau, S.-T. 2003. Global Conformal Surface Parameterization. In Proc. Symp. Geom. Proc., 127–137. Google ScholarDigital Library
19. Hertzmann, A., and Zorin, D. 2000. Illustrating Smooth Surfaces. In Proc. ACM/SIGGRAPH Conf., 517–526. Google ScholarDigital Library
20. Hildebrandt, K., Polthier, K., and Wardetzky, M. 2006. On the Convergence of Metric and Geometric Properties of Polyhedral Surfaces. Tech. Rep. ZR-05-24, Konrad-Zuse-Zentrum für Informationstechnik, Berlin.Google Scholar
21. Hirani, A. N. 2003. Discrete Exterior Calculus. PhD thesis, Caltech. Google ScholarDigital Library
22. Lefebvre, S., and Hoppe, H. 2006. Appearance-Space Texture Synthesis. ACM Trans. Graph. 25, 3, 541–548. Google ScholarDigital Library
23. Mebarki, A., Alliez, P., and Devillers, O. 2005. Farthest Point Seeding for Efficient Placement of Streamlines. In IEEE Visualization, 479–486.Google Scholar
24. Mercat, C. 2001. Discrete Riemann Surfaces and the Ising Model. Comm. in Math. Physics 218, 1, 177–216.Google ScholarCross Ref
25. Meyer, M., Desbrun, M., Schröder, P., and Barr, A. 2002. Discrete Differential-Geometry Operators for Triangulated 2-Manifolds. In Vis. and Math. III, H.-C. Hege and K. Polthier, Eds. Springer Verlag, 35–57.Google Scholar
26. Pedersen, H. K. 1995. Decorating Implicit Surfaces. In Proc. ACM/SIGGRAPH Conf., 291–300. Google ScholarDigital Library
27. Polthier, K., and Preuß, E. 2003. Identifying Vector Field Singularities using a Discrete Hodge Decomposition. In Vis. and Math. III, H. C. Hege and K. Polthier, Eds. Springer Verlag, 113–134.Google Scholar
28. Praun, E., Finkelstein, A., and Hoppe, H. 2000. Lapped Textures. In Proc. ACM/SIGGRAPH Conf., 465–470. Google ScholarDigital Library
29. Schlick, C. 1994. An Inexpensive BRDF Model for Physically-Based Rendering. Comp. Graph. Forum 13, 3, 233–246.Google ScholarCross Ref
30. Sorkine, O., Cohen-Or, D., Irony, D., and Toledo, S. 2005. Geometry-Aware Bases for Shape Approximation. IEEE Trans. Vis. Comp. Graph. 11, 2, 171–180. Google ScholarDigital Library
31. Theisel, H. 2002. Designing 2D Vector Fields of Arbitrary Topology. Comp. Graph. Forum 21, 3, 595–604.Google ScholarCross Ref
32. Toledo, S., 2003. TAUCS. Software at http://www.tau.ac.il/~stoledo/taucs/.Google Scholar
33. Tong, Y., Lombeyda, S., Hirani, A. N., and Desbrun, M. 2003. Discrete Multiscale Vector Field Decomposition. ACM Trans. Graph. 22, 3, 445–452. Google ScholarDigital Library
34. Tong, Y., Alliez, P., Cohen-Steiner, D., and Desbrun, M. 2006. Designing Quadrangulations with Discrete Harmonic Forms. In Proc. Symp. Geom. Proc., 201–210. Google ScholarDigital Library
35. Turk, G. 2001. Texture Synthesis on Surfaces. In Proc. ACM/SIGGRAPH Conf., 347–354. Google ScholarDigital Library
36. van Wijk, J. J. 1991. Spot Noise Texture Synthesis for Data Visualization. Comp. Graph. (Proc. of ACM/SIGGRAPH Conf.) 25, 4, 309–318. Google ScholarDigital Library
37. Wang, K., Weiwei, Tong, Y., Desbrun, M., and Schröder, P. 2006. Edge Subdivision Schemes and the Construction of Smooth Vector Fields. ACM Trans. Graph. 25, 3, 1041–1048. Google ScholarDigital Library
38. Wei, L.-Y., and Levoy, M. 2001. Texture Synthesis over Arbitrary Manifold Surfaces. In Proc. ACM/SIGGRAPH Conf., 355–360. Google ScholarDigital Library
39. Whitney, H. 1957. Geometric Integration Theory. Princeton University Press.Google Scholar
40. Zhang, E., Mischaikow, K., and Turk, G. 2006. Vector Field Design on Surfaces. ACM Trans. Graph. 25, 4, 1294–1326. Google ScholarDigital Library