“Deformable curve and surface finite-elements for free-form shape design” by Celniker and Gossard

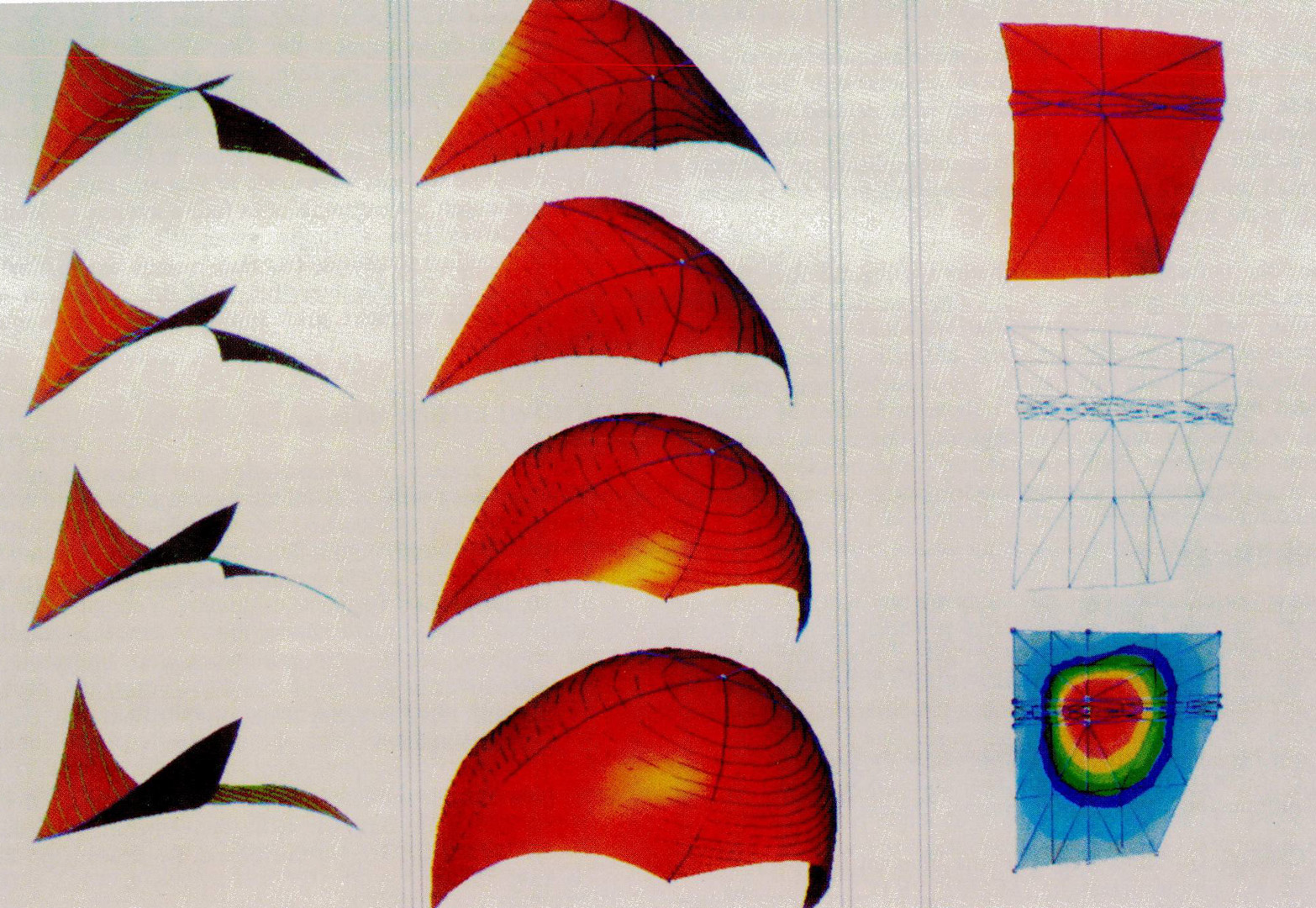
The finite element method is applied to generate primitives that build continuous deformable shapes designed to support a new free-form modeling paradigm. The primitives autonomously deform to minimize an energy functional subject to user controlled geometric constraints and loads. The approach requires less user input than conventional free-form modeling approaches because the shape can be parameterized independently of the number of degrees of freedom needed to describe the shape.Both a curve and a surface finite element are developed. The properties of these geometric primitives have been engineered to support an interactive three phase approach for defining very fair free-form shapes as found in automobiles, ship hulls and car bodies. The shape’s character lines or folds and edges are defined with deformable curve segments. These character lines are then “skinned” with a deformable surface. The final shape is sculpted interactively by applying loads to the surface to control the surface shape between character lines. Shapes created with this technique enjoy the advantage that they are already meshed for further finite element analysis.

1. Bloor, M.I.G. and Wilson, M.J., “Blend Design as a Boundary-Value Problem”, Theory and Practice of Geometric Modeling, Wolfgang Staber and Hans-Peter Seidel (Eds.), 1989
2. Celniker G., Gossard D., “Energy-Based Models for Free-Form Surface Shape Design”, ASME Design Automation Conference, Montreal Canada. Sep. 1989
3. Celniker G., ShapeWright: Finite Element Based Free- Form Shape Design, M.I.T. Ph.D., Dept. of Mechanical Engineering, September, 1990
4. Farin, Gerald and Sapidis, Nickolas, “Shape Representation of Sculpted Objects: the Fairness of Curves and Surfaces”, Proceeding of Sea Grant Conference, MIT, October, 1988
5. Farin, Gerald, Curves and Surfaces for Computer Aided Geometric Design, Academic Press Inc., Harcourt Brace Jovanovich Publishers, Boston, 1988
6. Hagen, H., and Schulze, G., “Automatic Smoothing with Geometric Surface Patches”, Computer Aided Geometric Design, Vol. 4, pp. 231-236, 1987
7. Kass, Michael and Witkin, Andrew, and Terzopoulos, Demetri, “Snakes” Active Contour Models”, International Journal of Computer Vision, 1988
8. Kallay, Michael and Ravani B., “Optimal twist vectors as a tool for interpolation a Network of curves with a minimal energy surface”, CAGD, 1990
9. Kjellander, J.A., “Smoothing of bicubic parametric surfaces”, Computer-Aided Design, Vol. 15, pp. 288- 293, 1983
10. Kjellander, J.A.P., “Smoothing of cubic parametric splines”, Computer-Aided Design, vol 15, No. 3, May, 1983
11. Lott, N.J. and Pullin, D.I., “Methods for fairing B- Spline surfaces”, Computer-Aided Design, vol. 20, no. 10, December, 1988
12. Nielson, G.M., “Some piecewise polynomial alternatives to splines in tension”, in Bamhill, RE and Riesenfeld, RF (eds) Computer Aided Geometric Design, Academic Press, 1974
13. Nowacki, H. and Reese, D., “Design and fairing of ship surfaces”, in Barnhill R.E. and Boehm, W. (eds), Surfaces in CAGD, North-Holland, Amsterdam, pp 121- 134, 1983
14. Pramila. A., “Ship Hull Surface design using finite elements”, Int. Shipbuild. Prog. Vol. 25 No. 284, pp. 97-I07, 1978
15. Sacks, E., and Stoops, D. and Roberts, A., “3-Draw: A Three Dimensional Computer Aided Design Tool”, proceedings IEEE international conference of systems, man, and cybernetics, pp 1194-1196, November 1989
16. Sapidis, N. and Farin, G., “Automatic fairing algorithm for B-spline curves”, Computer-Aided Design, Vol. 22, No. 2 pp. 121-129, March 1990
17. Schweikert, D.G., “An interpolation curve using a spline in tension”, Journal of Math and Phys. No 45, pp. 312-317, 1966
18. Strang, Gilbert, Introduction to Applied Mathematics, Wellesley-Cambridge Press, Massachusetts, 1986
19. Terzopoulos, Demetri and Plait, John and Barr, Alan and Fleischer, Kurt, “Elastic Deformable Models”, ACM, Computer Graphics, vol. 21, no. 4, July, 1987
20. Zienkiewicz, The Finite Element Method, third edition, McGraw-Hill Book Co., U.K., 1967