“Data-Free Learning of Reduced-Order Kinematics” by Sharp, Romero, Jacobson, Vouga, Kry, et al. …
Conference:
Type(s):
Title:
- Data-Free Learning of Reduced-Order Kinematics
Session/Category Title: Most Def: Fast, Large, and Learn Deformables
Presenter(s)/Author(s):
- Nicholas Sharp
- Cristian Romero
- Alec Jacobson
- Etienne Vouga
- Paul G. Kry
- David I. W. Levin
- Justin M. Solomon
Moderator(s):
Abstract:
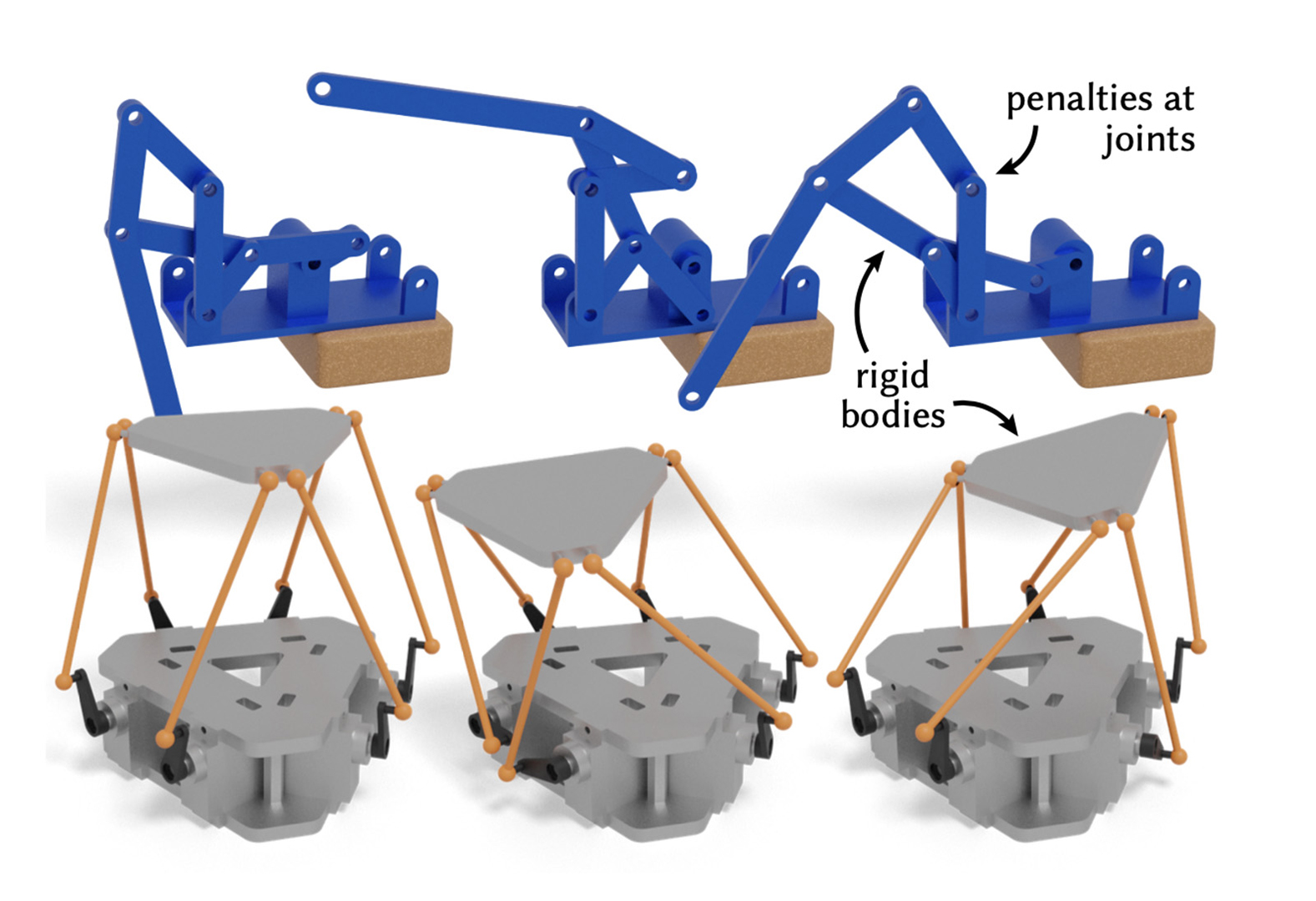
Physical systems ranging from elastic bodies to kinematic linkages are defined on high-dimensional configuration spaces, yet their typical low-energy configurations are concentrated on much lower-dimensional subspaces. This work addresses the challenge of identifying such subspaces automatically: given as input an energy function for a high-dimensional system, we produce a low-dimensional map whose image parameterizes a diverse yet low-energy submanifold of configurations. The only additional input needed is a single seed configuration for the system to initialize our procedure; no dataset of trajectories is required. We represent subspaces as neural networks that map a low-dimensional latent vector to the full configuration space, and propose a training scheme to fit network parameters to any system of interest. This formulation is effective across a very general range of physical systems; our experiments demonstrate not only nonlinear and very low-dimensional elastic body and cloth subspaces, but also more general systems like colliding rigid bodies and linkages. We briefly explore applications built on this formulation, including manipulation, latent interpolation, and sampling.
References:
1. S. S. An, T. Kim, and D. L. James. 2008. Optimizing Cubature for Efficient Integration of Subspace Deformations. ACM Trans. Graph. 27, 5, Article 165 (dec 2008), 10 pages. https://doi.org/10.1145/1409060.1409118
2. M. Arjovsky, S. Chintala, and L. Bottou. 2017. Wasserstein Generative Adversarial Networks. In Proceedings of the 34th International Conference on Machine Learning(Proceedings of Machine Learning Research), Doina Precup and Yee Whye Teh (Eds.). Vol. 70. PMLR, 214–223. https://proceedings.mlr.press/v70/arjovsky17a.html
3. J. Barbič and D. L. James. 2005. Real-Time Subspace Integration for St. Venant-Kirchhoff Deformable Models. ACM Trans. Graph. 24, 3 (jul 2005), 982–990. https://doi.org/10.1145/1073204.1073300
4. P. Benner, S. Gugercin, and K. Willcox. 2015. A survey of projection-based model reduction methods for parametric dynamical systems. SIAM review 57, 4 (2015), 483–531.
5. H. Bertiche, M. Madadi, and S. Escalera. 2021. PBNS: physically based neural simulation for unsupervised garment pose space deformation. ACM Transactions on Graphics (TOG) 40, 6 (2021), 1–14.
6. H. Bertiche, M. Madadi, and S. Escalera. 2022. Neural Cloth Simulation. ACM Transactions on Graphics (TOG) 41, 6 (2022), 1–14.
7. F. Boukouvala, Y. Gao, F. Muzzio, and M. G. Ierapetritou. 2013. Reduced-order discrete element method modeling. Chemical Engineering Science 95 (2013), 12–26.
8. J. Bradbury, R. Frostig, P. Hawkins, M. J. Johnson, C. Leary, D. Maclaurin, G. Necula, A. Paszke, J. VanderPlas, S. Wanderman-Milne, and Q. Zhang. 2018. JAX: composable transformations of Python+NumPy programs. http://github.com/google/jax
9. C. Brandt, E. Eisemann, and K. Hildebrandt. 2018. Hyper-reduced projective dynamics. ACM Transactions on Graphics (TOG) 37, 4 (2018), 1–13.
10. C. Brandt, C. von Tycowicz, and K. Hildebrandt. 2016. Geometric flows of curves in shape space for processing motion of deformable objects. In Computer Graphics Forum, Vol. 35. Wiley Online Library, 295–305.
11. M. M. Bronstein, J. Bruna, T. Cohen, and P. Veličković. 2021. Geometric deep learning: Grids, groups, graphs, geodesics, and gauges. arXiv preprint arXiv:2104.13478 (2021).
12. M. G. Choi and H.-S. Ko. 2005. Modal warping: Real-time simulation of large rotational deformation and manipulation. IEEE Transactions on Visualization and Computer Graphics 11, 1 (2005), 91–101.
13. Y. Du, K. Collins, J. Tenenbaum, and V. Sitzmann. 2021. Learning signal-agnostic manifolds of neural fields. Advances in Neural Information Processing Systems 34 (2021), 8320–8331.
14. L. Fulton, V. Modi, D. Duvenaud, D. I. W. Levin, and A. Jacobson. 2019. Latent-space Dynamics for Reduced Deformable Simulation. Computer Graphics Forum (2019).
15. H. Gao, L. Sun, and J.-X. Wang. 2021. Super-resolution and denoising of fluid flow using physics-informed convolutional neural networks without high-resolution labels. Physics of Fluids 33, 7 (2021), 073603.
16. E. Grinspun, A. N. Hirani, M. Desbrun, and P. Schröder. 2003. Discrete shells. In Proceedings of the 2003 ACM SIGGRAPH/Eurographics symposium on Computer animation. Citeseer, 62–67.
17. R. Grzeszczuk, D. Terzopoulos, and G. Hinton. 1998. Neuroanimator: Fast neural network emulation and control of physics-based models. In Proceedings of the 25th annual conference on Computer graphics and interactive techniques. 9–20.
18. F. Hahn, S. Martin, B. Thomaszewski, R. Sumner, S. Coros, and M. Gross. 2012. Rig-space physics. ACM transactions on graphics (TOG) 31, 4 (2012), 1–8.
19. F. Hahn, B. Thomaszewski, S. Coros, R. W. Sumner, F. Cole, M. Meyer, T. DeRose, and M. Gross. 2014. Subspace clothing simulation using adaptive bases. ACM Transactions on Graphics (TOG) 33, 4 (2014), 1–9.
20. K. Hildebrandt, C. Schulz, C. v. Tycowicz, and K. Polthier. 2011. Interactive surface modeling using modal analysis. ACM Transactions on Graphics (TOG) 30, 5 (2011), 1–11.
21. D. Holden, B. C. Duong, S. Datta, and D. Nowrouzezahrai. 2019. Subspace Neural Physics: Fast Data-Driven Interactive Simulation. In Proceedings of the 18th Annual ACM SIGGRAPH/Eurographics Symposium on Computer Animation(SCA ’19). Association for Computing Machinery, New York, NY, USA, Article 6, 12 pages. https://doi.org/10.1145/3309486.3340245
22. D. L. James, J. Barbič, and D. K. Pai. 2006. Precomputed acoustic transfer: output-sensitive, accurate sound generation for geometrically complex vibration sources. ACM Transactions on Graphics (TOG) 25, 3 (2006), 987–995.
23. D. L. James and D. K. Pai. 2002. DyRT: Dynamic Response Textures for Real Time Deformation Simulation with Graphics Hardware. ACM Trans. Graph. 21, 3 (jul 2002), 582–585. https://doi.org/10.1145/566654.566621
24. T. Kim. 2020. A Finite Element Formulation of Baraff-Witkin Cloth. In Computer Graphics Forum, Vol. 39. Wiley Online Library, 171–179.
25. D. P. Kingma and J. Ba. 2014. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980 (2014).
26. D. Kochkov, J. A. Smith, A. Alieva, Q. Wang, M. P. Brenner, and S. Hoyer. 2021. Machine learning–accelerated computational fluid dynamics. Proceedings of the National Academy of Sciences 118, 21 (2021).
27. C.-H. Lee and J.-S. Chen. 2013. Proper orthogonal decomposition-based model order reduction via radial basis functions for molecular dynamics systems. International journal for numerical methods in engineering 96, 10 (2013), 599–627.
28. K. Lee and K. T. Carlberg. 2020. Model reduction of dynamical systems on nonlinear manifolds using deep convolutional autoencoders. J. Comput. Phys. 404 (2020), 108973.
29. Y. Li, J. Wu, R. Tedrake, J. B. Tenenbaum, and A. Torralba. 2018. Learning particle dynamics for manipulating rigid bodies, deformable objects, and fluids. arXiv preprint arXiv:1810.01566 (2018).
30. Y. Li, J. Wu, J.-Y. Zhu, J. B. Tenenbaum, A. Torralba, and R. Tedrake. 2019. Propagation networks for model-based control under partial observation. In 2019 International Conference on Robotics and Automation (ICRA). IEEE, 1205–1211.
31. H. Lin, F. M. Chitalu, and T. Komura. 2022. Isotropic ARAP energy using Cauchy-Green invariants. ACM Transactions on Graphics (TOG) 41, 6 (2022), 1–14.
32. D. C. Liu and J. Nocedal. 1989. On the Limited Memory BFGS Method for Large Scale Optimization. MATHEMATICAL PROGRAMMING 45 (1989), 503–528.
33. A. K. Noor and J. M. Peters. 1980. Reduced basis technique for nonlinear analysis of structures. Aiaa journal 18, 4 (1980), 455–462.
34. T. Pfaff, M. Fortunato, A. Sanchez-Gonzalez, and P. W. Battaglia. 2020. Learning mesh-based simulation with graph networks. arXiv preprint arXiv:2010.03409 (2020).
35. C. R. Qi, H. Su, K. Mo, and L. J. Guibas. 2017. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE conference on computer vision and pattern recognition. 652–660.
36. C. Romero, D. Casas, J. Pérez, and M. Otaduy. 2021. Learning contact corrections for handle-based subspace dynamics. ACM Transactions on Graphics (TOG) 40, 4 (2021), 1–12.
37. C. Romero, M. A. Otaduy, D. Casas, and J. Perez. 2020. Modeling and estimation of nonlinear skin mechanics for animated avatars. In Computer Graphics Forum, Vol. 39. Wiley Online Library, 77–88.
38. I. Santesteban, M. A. Otaduy, and D. Casas. 2022. SNUG: Self-Supervised Neural Dynamic Garments. IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (2022).
39. A. A. Shabana. 1991. Theory of vibration. Vol. 2. Springer.
40. S. Shen, Y. Yang, T. Shao, H. Wang, C. Jiang, L. Lan, and K. Zhou. 2021. High-Order Differentiable Autoencoder for Nonlinear Model Reduction. ACM Trans. Graph. 40, 4, Article 68 (jul 2021), 15 pages. https://doi.org/10.1145/3450626.3459754
41. B. Smith, F. D. Goes, and T. Kim. 2018. Stable Neo-Hookean Flesh Simulation. ACM Trans. Graph. 37, 2, Article 12 (mar 2018), 15 pages. https://doi.org/10.1145/3180491
42. B. Smith, F. D. Goes, and T. Kim. 2019. Analytic eigensystems for isotropic distortion energies. ACM Transactions on Graphics (TOG) 38, 1 (2019), 1–15.
43. S. G. Srinivasan, Q. Wang, J. Rojas, G. Klár, L. Kavan, and E. Sifakis. 2021. Learning active quasistatic physics-based models from data. ACM Transactions on Graphics (TOG) 40, 4 (2021), 1–14.
44. J. Tompson, K. Schlachter, P. Sprechmann, and K. Perlin. 2017. Accelerating eulerian fluid simulation with convolutional networks. In International Conference on Machine Learning. PMLR, 3424–3433.
45. C. Von-Tycowicz, C. Schulz, H.-P. Seidel, and K. Hildebrandt. 2015. Real-Time Nonlinear Shape Interpolation. ACM Trans. Graph. 34, 3, Article 34 (may 2015), 10 pages. https://doi.org/10.1145/2729972
46. Y. Wang, Y. Sun, Z. Liu, S. E. Sarma, M. M. Bronstein, and J. M. Solomon. 2019. Dynamic graph cnn for learning on point clouds. Acm Transactions On Graphics (tog) 38, 5 (2019), 1–12.
47. Y. Xie, T. Takikawa, S. Saito, O. Litany, S. Yan, N. Khan, F. Tombari, J. Tompkin, V. Sitzmann, and S. Sridhar. 2022. Neural Fields in Visual Computing and Beyond. Computer Graphics Forum (2022). https://doi.org/10.1111/cgf.14505
48. Y. Yang, D. Li, W. Xu, Y. Tian, and C. Zheng. 2015. Expediting precomputation for reduced deformable simulation. ACM Trans. Graph 34, 6 (2015).
49. M. Zhang, T. Y. Wang, D. Ceylan, and N. J. Mitra. 2021. Dynamic Neural Garments. ACM Trans. Graph. 40, 6, Article 235 (dec 2021), 15 pages. https://doi.org/10.1145/3478513.3480497
50. M. Zheng, Y. Zhou, D. Ceylan, and J. Barbic. 2021. A deep emulator for secondary motion of 3d characters. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 5932–5940.