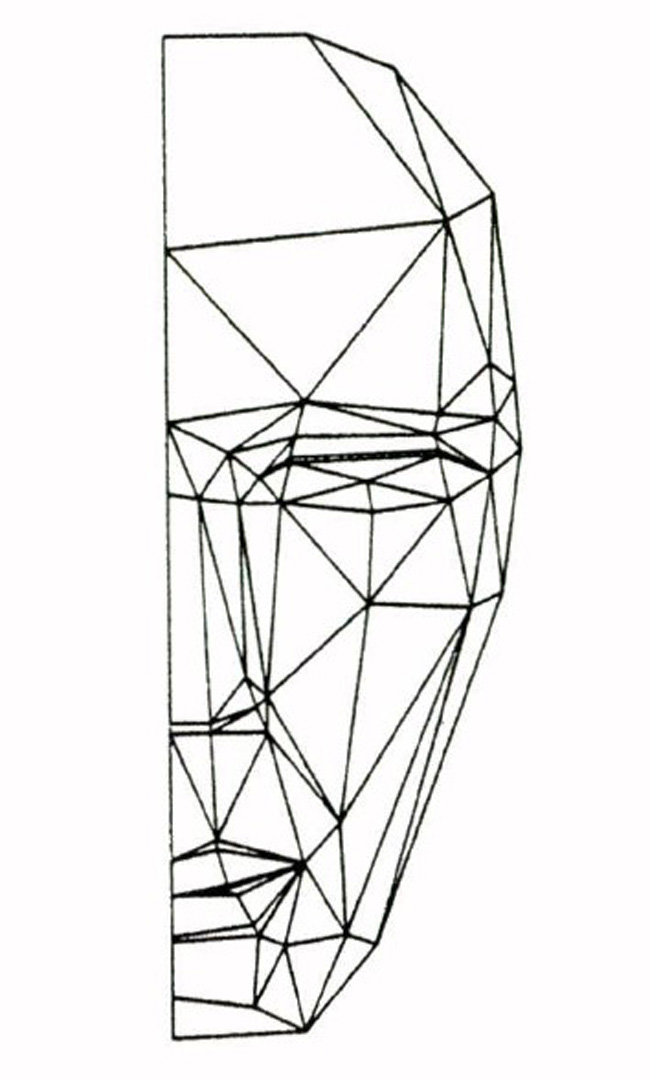
“Creating volume models from edge-vertex graphs” by Hanrahan

The design of complex geometric models has been and will continue to be one of the limiting factors in computer graphics. A careful enumeration of the properties of topologically correct models, so that they may be automatically enforced, can greatly speed this process. An example of the problems inherent in these methods is the “wire frame” problem, the automatic generation of a volume model from an edge-vertex graph. The solution to this problem has many useful applications in geometric modelling and scene recognition. This paper shows that the “wire frame” problem is equivalent to finding the embedding of a graph on a closed orientable surface. Such an embedding satisfies all the topological properties of physical volumes. Unfortunately graphical embeddings are not necessarily unique. But when we restrict the embedding surface so that it is equivalent to a sphere, and require that the input graph be three-connected, the resulting object is unique. Given these restrictions there exists a linear time algorithm to automatically convert the “wire frame” to the winged edge representation, a very powerful data structure. Applications of this algorithm are discussed and several examples shown.

1. Baumgart, B. G. Geometric Modelling for Computer Vision. Stanford Artificial Intelligence Project, Research Memo No. 249. Computer Sciences Department, Stanford University. 1974.
2. Catmull, E., and Clark, J. Recursively generated B-spline surfaces on arbitrary meshes. Computer Aided Design. 10(6) 1978.
3. Demoucron, G., Malgrange, Y., and Pertuiset, R. Graphes plainaires: reconaissance et constructien de representations planares topologiques. Rev. Francaise Recherche Operationelle. 8 pp. 33-47. 1964.
4. Edmonds, J. A Combinatorial Representation for Polyhedral Surfaces. Notices Amer. Math. Soc. 7 p. 646 1960.
5. Falk, G. Computer Interpretation of Imperfect Line Data as a Three Dimensional Scene. Stanford Artificial Intelligence Project, Research Memo No. 132. Computer Sciences Department, Stanford University. 1970.
6. Filotti, I. S., Miller, G. L. and Reif J. On Determining the Genus of a Graph in O(vO(g)) Steps. Eleventh Annual Symposium on the Theory of Computing. pp. 27-37 1979.
7. Ganter, M. A. Techniques for Converting Wire-Frame to Solid-Geometric Representations. Masters Thesis. University of Wisconsin – Madison. 1981.
8. Liardet, M. PICAX – Polyhedron Input to the Computer Using an Axonometric Drawing. Interactive Techniques in Computer Aided Design. pp. 344-355 1978.
9. Markowsky, G. and Wesley, M.A. Fleshing out Wire Frames. IBM J. Res. Develop. 24(5):582-597 1980.
10. Rubin, F. An Improved Algorithm for Testing Graph Planarity. IEEE Trans. Comp. C24:113-121 1975.
11. Waltz, D. L. Generating Semantic Descriptions from Line Drawings of Scenes with Shadows. Ph.D. thesis. Department of Electrical Engineering, Massachusetts Institute of Technology. Cambridge, Mass.