“Continuous projection for fast L1 reconstruction” by Preiner, Mattausch, Arikan, Pajarola and Wimmer
Conference:
Type(s):
Title:
- Continuous projection for fast L1 reconstruction
Session/Category Title: Points & Reconstruction
Presenter(s)/Author(s):
Abstract:
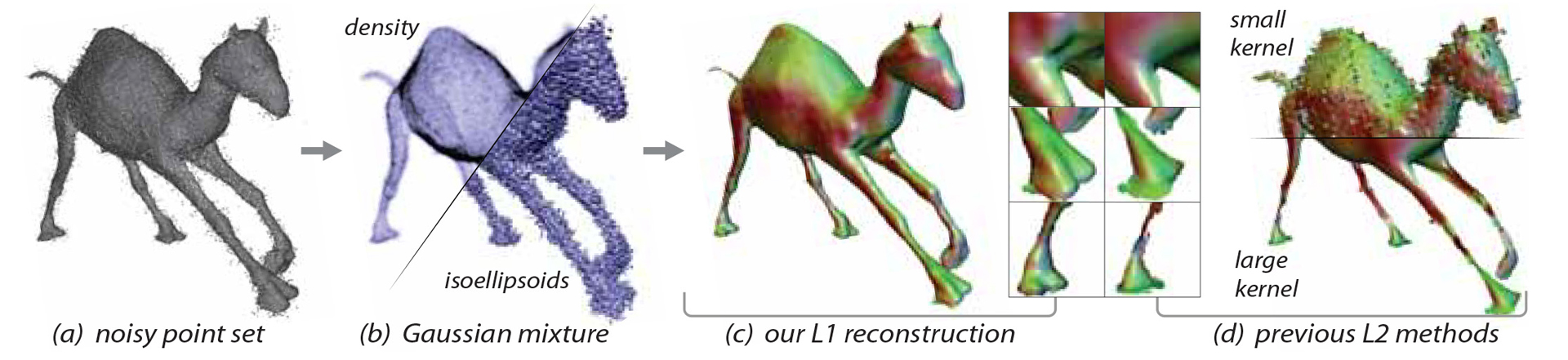
With better and faster acquisition devices comes a demand for fast robust reconstruction algorithms, but no L1-based technique has been fast enough for online use so far. In this paper, we present a novel continuous formulation of the weighted locally optimal projection (WLOP) operator based on a Gaussian mixture describing the input point density. Our method is up to 7 times faster than an optimized GPU implementation of WLOP, and achieves interactive frame rates for moderately sized point clouds. We give a comprehensive quality analysis showing that our continuous operator achieves a generally higher reconstruction quality than its discrete counterpart. Additionally, we show how to apply our continuous formulation to spherical mixtures of normal directions, to also achieve a fast robust normal reconstruction.
References:
1. Alexa, M., Behr, J., Cohen-Or, D., Fleishman, S., Levin, D., and Silva, C. T. 2003. Computing and rendering point set surfaces. IEEE Transactions on Visualization and Computer Graphics 9, 1 (Jan.), 3–15. Google ScholarDigital Library
2. Amenta, N., and Kil, Y. J. 2004. Defining point-set surfaces. ACM Trans. Graph. 23, 3 (Aug.), 264–270. Google ScholarDigital Library
3. Avron, H., Sharf, A., Greif, C., and Cohen-Or, D. 2010. L1-sparse reconstruction of sharp point set surfaces. ACM Trans. Graph. 29, 5 (Nov.), 135:1–135:12. Google ScholarDigital Library
4. Banerjee, A., Dhillon, I. S., Ghosh, J., and Sra, S. 2005. Clustering on the unit hypersphere using von mises-fisher distributions. J. Mach. Learn. Res. 6 (Dec.), 1345–1382. Google ScholarDigital Library
5. Berger, M., Levine, J. A., Nonato, L. G., Taubin, G., and Silva, C. T. 2013. A benchmark for surface reconstruction. ACM Trans. Graph. 32, 2 (Apr.), 20:1–20:17. Google ScholarDigital Library
6. Boulch, A., and Marlet, R. 2012. Fast and robust normal estimation for point clouds with sharp features. Computer Graphics Forum 31, 5, 1765–1774. Google ScholarDigital Library
7. Brown, B. J., and Rusinkiewicz, S. 2007. Global non-rigid alignment of 3-d scans. ACM Trans. Graph. 26, 3 (July). Google ScholarDigital Library
8. Carr, J. C., Beatson, R. K., Cherrie, J. B., Mitchell, T. J., Fright, W. R., McCallum, B. C., and Evans, T. R. 2001. Reconstruction and representation of 3d objects with radial basis functions. In Proceedings of Conference on Computer graphics and interactive techniques, ACM, SIGGRAPH ’01, 67–76. Google ScholarDigital Library
9. Dempster, A. P., Laird, N. M., and Rubin, D. B. 1977. Maximum likelihood from incomplete data via the em algorithm. Journal of the Royal Statistical Society Series B 39, 1, 1–38.Google ScholarCross Ref
10. Dey, T. K., and Sun, J. 2006. Normal and feature approximations from noisy point clouds. In Proceedings of Conference on Foundations of Software Technology and Theoretical Computer Science, vol. 4337 of Lecture Notes in Computer Science, 21–32. Google ScholarDigital Library
11. Fleishman, S., Cohen-Or, D., and Silva, C. T. 2005. Robust moving least-squares fitting with sharp features. ACM Trans. Graph. 24, 3 (July), 544–552. Google ScholarDigital Library
12. Garcia, V., Nielsen, F., and Nock, R. 2010. Hierarchical Gaussian mixture model. In IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP).Google Scholar
13. Hartley, R., Aftab, K., and Trumpf, J. 2011. L1 rotation averaging using the weiszfeld algorithm. In Proceedings of IEEE Conference on Computer Vision and Pattern Recognition, CVPR ’11, 3041–3048. Google ScholarDigital Library
14. Hoppe, H., DeRose, T., Duchamp, T., McDonald, J., and Stuetzle, W. 1992. Surface reconstruction from unorganized points. In Proceedings of the 19th annual conference on Computer graphics and interactive techniques, ACM, SIGGRAPH ’92, 71–78. Google ScholarDigital Library
15. Huang, H., Li, D., Zhang, H., Ascher, U., and Cohen-Or, D. 2009. Consolidation of unorganized point clouds for surface reconstruction. ACM Trans. Graph. 28, 5 (Dec.), 176:1–176:7. Google ScholarDigital Library
16. Izadi, S., Kim, D., Hilliges, O., Molyneaux, D., Newcombe, R., Kohli, P., Shotton, J., Hodges, S., Freeman, D., Davison, A., and Fitzgibbon, A. 2011. Kinect-fusion: real-time 3d reconstruction and interaction using a moving depth camera. In Proceedings of Symposium on User Interface Software and Technology, ACM, UIST ’11, 559–568. Google ScholarDigital Library
17. Jakob, W., Regg, C., and Jarosz, W. 2011. Progressive expectation–maximization for hierarchical volumetric photon mapping. Computer Graphics Forum 30, 4 (June). Google ScholarDigital Library
18. Kalogerakis, E., Simari, P., Nowrouzezahrai, D., and Singh, K. 2007. Robust statistical estimation of curvature on discretized surfaces. In Proceedings of the Eurographics Symposium on Geometry Processing, SGP ’07, 13–22. Google ScholarDigital Library
19. Kazhdan, M., and Hoppe, H. 2013. Screened poisson surface reconstruction. ACM Trans. Graph. 32, 3 (July), 29:1–29:13. Google ScholarDigital Library
20. Kazhdan, M., Bolitho, M., and Hoppe, H. 2006. Poisson surface reconstruction. In Eurographics Symposium on Geometry Processing, SGP ’06, 61–70. Google ScholarDigital Library
21. Li, B., Schnabel, R., Klein, R., Cheng, Z., Dang, G., and Shiyao, J. 2010. Robust normal estimation for point clouds with sharp features. Computers & Graphics 34, 2 (Apr.), 94–106. Google ScholarDigital Library
22. Liao, B., Xiao, C., Jin, L., and Fu, H. 2013. Efficient feature-preserving local projection operator for geometry reconstruction. Computer-Aided Design 45, 5, 861–874.Google ScholarCross Ref
23. Lipman, Y., Cohen-Or, D., Levin, D., and Tal-Ezer, H. 2007. Parameterization-free projection for geometry reconstruction. ACM Trans. Graph. 26, 3 (July). Google ScholarDigital Library
24. Mardia, K., and Jupp, P. 2009. Directional Statistics. Wiley Series in Probability and Statistics. Wiley.Google Scholar
25. Oztireli, C., Guennebaud, G., and Gross, M. 2009. Feature preserving point set surfaces based on non-linear kernel regression. Computer Graphics Forum 28, 2.Google ScholarCross Ref
26. Petersen, K. B., and Pedersen, M. S., 2012. The matrix cookbook, nov. Version 20121115.Google Scholar
27. Preiner, R., Jeschke, S., and Wimmer, M. 2012. Auto Splats: Dynamic point cloud visualization on the GPU. In Proceedings of Eurographics Symposium on Parallel Graphics and Visualization, 139–148.Google Scholar
28. Vasconcelos, N. 1998. Learning mixture hierarchies. In Proceedings of Advances in Neural Information Processing Systems, MIT Press, NIPS’98, 606–612. Google ScholarDigital Library
29. Walter, B., Bala, K., Kulkarni, M., and Pingali, K. 2008. Fast agglomerative clustering for rendering. In IEEE Symposium on Interactive Ray Tracing, 81–86.Google Scholar
30. Zheng, Q., Sharf, A., Wan, G., Li, Y., Mitra, N. J., Cohen-Or, D., and Chen, B. 2010. Non-local scan consolidation for 3d urban scenes. ACM Trans. Graph. 29 (July), 94:1–94:9. Google ScholarDigital Library
31. Zhou, K., Hou, Q., Wang, R., and Guo, B. 2008. Real-time kd-tree construction on graphics hardware. ACM Trans. Graph. 27, 5 (Dec.), 126:1–126:11. Google ScholarDigital Library