“Contact and friction simulation for computer graphics” Chaired by
Conference:
Type(s):
Title:
- Contact and friction simulation for computer graphics
Presenter(s)/Author(s):
Entry Number:
- 03
Abstract:
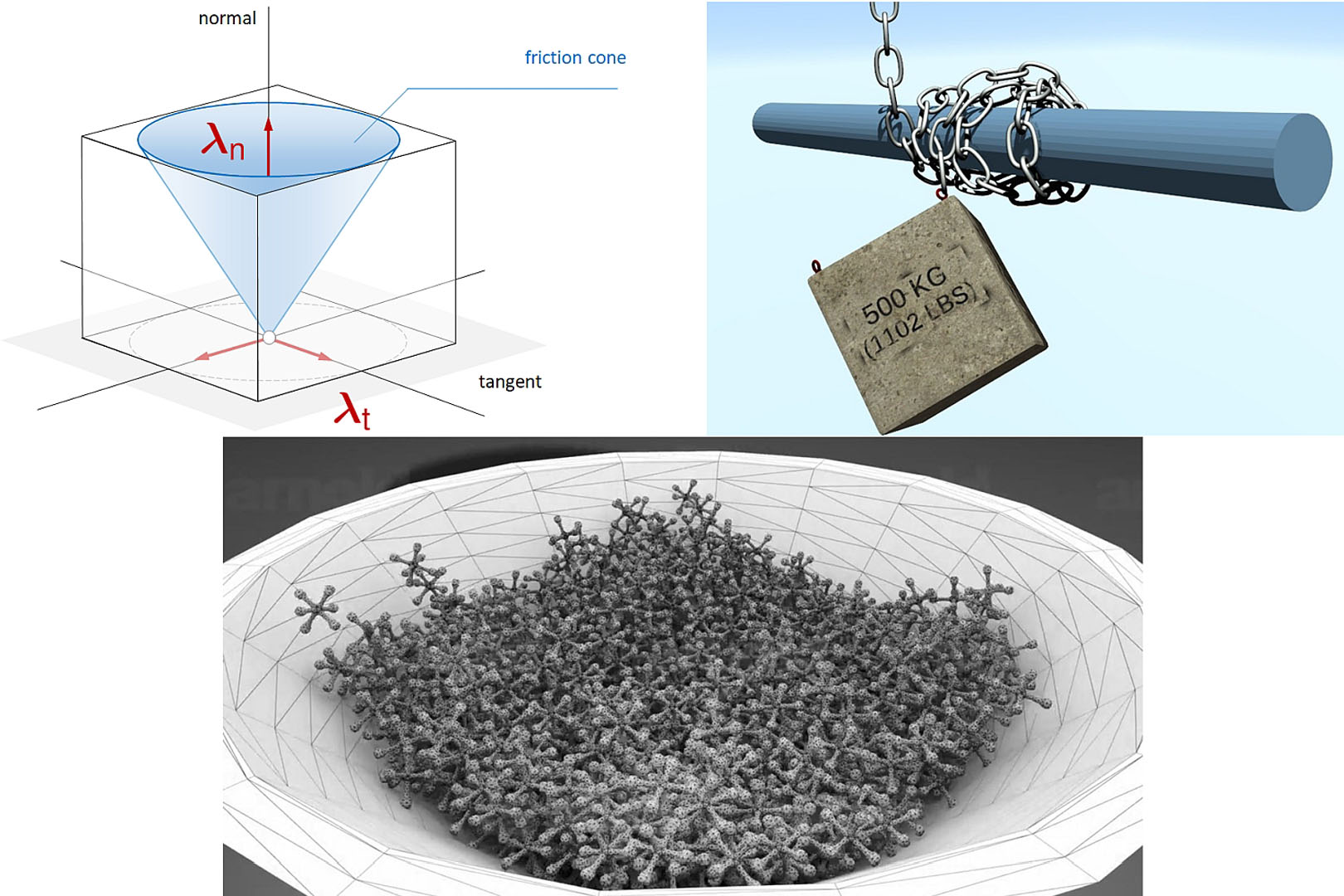
Efficient simulation of contact is of interest for numerous physics-based animation applications. For instance, virtual reality training, video games, rapid digital prototyping, and robotics simulation are all examples of applications that involve contact modeling and simulation. However, despite its extensive use in modern computer graphics, contact simulation remains one of the most challenging problems in physics-based animation.
This course covers fundamental topics on the nature of contact modeling and simulation for computer graphics. Specifically, we provide mathematical details about formulating contact as a complementarity problem in rigid body and soft body animations. We briefly cover several approaches for contact generation using discrete collision detection. Then, we present a range of numerical techniques for solving the associated LCPs and NCPs. The advantages and disadvantages of each technique are further discussed in a practical manner, and best practices for implementation are discussed. Finally, we conclude the course with several advanced topics such as methods for soft body contact problems, barrier functions, and anisotropic friction modeling. Programming examples are provided in our appendix as well as on the course website to accompany the course notes.
References:
- V. Acary, F. Cadoux, C. Lemaréchal, and J. Malick. 2011. A formulation of the linear discrete Coulomb friction problem via convex optimization. ZAMM-Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik 91, 2 (2011), 155–175.
- S. Ainsley, E. Vouga, E. Grinspun, and R. Tamstorf. 2012. Speculative parallel asynchronous contact mechanics. ACM Trans. Graph. 31, 6, Article 151 (Nov. 2012), 8 pages.
- S. Andrews, K. Erleben, P. G. Kry, and M. Teichmann. 2017. Constraint reordering for iterative multi-body simulation with contact. In ECCOMAS ’17: Proc. of the Multibody Dynamics 2007 ECCOMAS Thematic Conference. ECCOMAS, Prague, Czech Republic.
- S. Andrews, L. Nassif, K. Erleben, and P. G. Kry. 2021. Coupling Friction with Visual Appearance. Proc. of the ACM on Computer Graphics and Interactive Techniques 4, 3 (2021), 20.
- M. Anitescu and G. D. Hart. 2004. A constraint-stabilized time-stepping approach for rigid multibody dynamics with joints, contact and friction. Intl. Journal for Numerical Methods in Engineering 60, 14 (2004), 2335–2371.
- M. Anitescu and F. A. Potra. 1997. Formulating Dynamic Multi-Rigid-Body Contact Problems with Friction as Solvable Linear Complementarity Problems. Nonlinear Dynamics 14 (1997), 231–247. Issue 3.
- M. Anitescu and A. Tasora. 2010. An iterative approach for cone complementarity problems for nonsmooth dynamics. Computational Optimization and Applications 47, 2 (October 2010), 207–235.
- L. Armijo. 1966. Minimization of functions having Lipschitz continuous first partial derivatives. Pacific J. Math. 16, 1 (1966), 1 — 3.
- D. Baraff. 1989. Analytical Methods for Dynamic Simulation of Non-Penetrating Rigid Bodies. In Proceedings of the 16th Annual Conference on Computer Graphics and Interactive Techniques (SIGGRAPH ’89). Association for Computing Machinery, New York, NY, USA, 223–232.
- D. Baraff. 1993. Issues in computing contact forces for nonpenetrating rigid bodies. Algorithmica. An Intl. Journal in Computer Science 10, 2–4 (1993), 292–352.
- D. Baraff. 1994. Fast contact force computation for nonpenetrating rigid bodies. In Proc. of the 21st Annual Conference on Computer Graphics and Interactive Techniques (SIGGRAPH ’94). ACM, New York, NY, USA, 23–34.
- D. Baraff and A. Witkin. 1998. Large Steps in Cloth Simulation. In Proc. of the 25th Annual Conference on Computer Graphics and Interactive Techniques (SIGGRAPH ’98). ACM, New York, NY, USA, 43–54.
- A. W. Bargteil, T. Shinar, and P. G. Kry. 2020. An Introduction to Physics-Based Animation. In SIGGRAPH Asia 2020 Courses (Virtual Event) (SA ’20). ACM, New York, NY, USA, Article 5, 57 pages.
- C. Batty, F. Bertails, and R. Bridson. 2007. A fast variational framework for accurate solid-fluid coupling. ACM Trans. Graph. 26, Article 100 (July 2007). Issue 3.
- J. Baumgarte. 1972. Stabilization of constraints and integrals of motion in dynamical systems. Computer Methods in Applied Mechanics and Engineering 1, 1 (1972), 1–16.
- J. Bender, K. Erleben, and J. Trinkle. 2014. Interactive Simulation of Rigid Body Dynamics in Computer Graphics. Comp. Graph. Forum 33, 1 (2014), 246–270.
- S. Bouaziz, S. Martin, T. Liu, L. Kavan, and M. Pauly. 2014. Projective Dynamics: Fusing Constraint Projections for Fast Simulation. ACM Trans. Graph. 33, 4 (July 2014), 154:1–154:11.
- S. Boyd and L. Vandenberghe. 2004. Convex Optimization. Cambridge University Press, Cambridge.
- R. Bridson, R. Fedkiw, and J. Anderson. 2002. Robust Treatment of Collisions, Contact and Friction for Cloth Animation. ACM Trans. Graph. 21, 3 (July 2002), 594–603.
- T. Brochu, E. Edwards, and R. Bridson. 2012. Efficient Geometrically Exact Continuous Collision Detection. ACM Trans. Graph. 31, 4, Article 96 (July 2012), 7 pages.
- D. T. Chen and D. Zeltzer. 1992. Pump It up: Computer Animation of a Biomechanically Based Model of Muscle Using the Finite Element Method. In Proc. of the 19th Annual Conference on Computer Graphics and Interactive Techniques (SIGGRAPH ’92). ACM, New York, NY, USA, 89–98.
- Y. Chen, M. Li, L. Lan, H. Su, Y. Yang, and C. Jiang. 2022. A Unified Newton Barrier Method for Multibody Dynamics. ACM Trans. Graph. (SIGGRAPH) 41, 4, Article 66 (2022).
- Z. Chen, R. Feng, and H. Wang. 2013. Modeling Friction and Air Effects Between Cloth and Deformable Bodies. ACM Trans. Graph. 32, 4, Article 88 (July 2013), 8 pages.
- M. B. Cline and D. K. Pai. 2003. Post-stabilization for rigid body simulation with contact and constraints. In 2003 IEEE Intl. Conference on Robotics and Automation, Vol. 3. IEEE, Taipei, Taiwan, 3744–3751.
- CM Labs Simulations. 2017. Theory Guide: Vortex Software’s Multibody Dynamics Engine. Technical Report. https://www.cm-labs.com/vortexstudiodocumentation/Vortex_User_Documentation/Content/Concepts/theoryguide.html
- R. Cottle. 1968. Complementary Pivot Theory of Mathematical Programming. Linear Algebra and Its Applications 1 (1968), 103–125.
- R. Cottle, J.-S. Pang, and R. E. Stone. 1992. The Linear Complementarity Problem. Academic Press, Boston.
- E. Coumans. 2005. The Bullet Physics Library. http://www.pybullet.org.
- H. Courtecuisse, J. Allard, C. Duriez, and S. Cotin. 2011. Preconditioner-Based Contact Response and Application to Cataract Surgery. In Proceedings of the 14th International Conference on Medical Image Computing and Computer-Assisted Intervention – Volume Part I (Toronto, Canada) (MICCAI’11). Springer-Verlag, Berlin, Heidelberg, 315–322.
- G. Daviet. 2020. Simple and Scalable Frictional Contacts for Thin Nodal Objects. ACM Trans. Graph. 39, 4, Article 61 (July 2020), 16 pages.
- G. Daviet, F. Bertails-Descoubes, and L. Boissieux. 2011. A hybrid iterative solver for robustly capturing coulomb friction in hair dynamics. ACM Trans. Graph. 30, 6, Article 139 (Dec. 2011), 12 pages.
- A. Enzenhoefer, N. Lefebvre, and S. Andrews. 2019. Efficient Block Pivoting for Multibody Simulations with Contact. In Proc. of the 2019 ACM SIGGRAPH Symposium on Interactive 3D Graphics and Games (Montreal, Quebec, Canada) (I3D ’19). ACM, New York, NY, USA, Article 2, 9 pages.
- K. Erleben. 2005. Stable, Robust, and Versatile Multibody Dynamics Animation. Ph.D. Dissertation. Department of Computer Science, University of Copenhagen (DIKU).
- K. Erleben. 2007. Velocity-Based Shock Propagation for Multibody Dynamics Animation. ACM Trans. Graph. 26, 2 (June 2007), 12–es.
- K. Erleben. 2017. Rigid Body Contact Problems Using Proximal Operators. In Proc. of the 2017 ACM SIGGRAPH / Eurographics Symposium on Computer Animation (Los Angeles, California) (SCA ’17). ACM, New York, NY, USA, Article 13, 12 pages.
- K. Erleben, M. Andersen, N. S., and S. M. 2011. num4lcp. https://github.com/erleben/num4lcp.
- K. Erleben, M. Macklin, S. Andrews, and P. G. Kry. 2020. The Matchstick Model for Anisotropic Friction Cones. Comp. Graph. Forum 39, 1 (2020), 450–461.
- Z. Ferguson et al. 2020. IPC Toolkit. https://ipc-sim.github.io/ipc-toolkit/
- Z. Ferguson, M. Li, T. Schneider, F. Gil-Ureta, T. Langlois, C. Jiang, D. Zorin, D. M. Kaufman, and D. Panozzo. 2021. Intersection-Free Rigid Body Dynamics. ACM Trans. Graph. (SIGGRAPH) 40, 4, Article 183 (jul 2021), 16 pages.
- M. C. Ferris and T. S. Munson. 1999. Interfaces to PATH 3.0: Design, Implementation and Usage. Comput. Optim. Appl. 12 (January 1999), 207–227. Issue 1–3.
- A. Fischer. 1992. A special newton-type optimization method. Optimization 24, 3–4 (1992), 269–284.
- M. Foerg, T. Geier, L. Neumann, and H. Ulbrich. 2006. r-Factor Strategies for the Augmented Lagrangian Approach in Multi-Body Contact Mechanics. In III European Conference on Computational Mechanics. Springer Netherlands, Dordrecht, NL, 316.
- M. Fratarcangeli and F. Pellacini. 2015. Scalable Partitioning for Parallel Position Based Dynamics. Comput. Graph. Forum 34, 2 (May 2015), 405–413.
- S. F. Frisken, R. N. Perry, A. P. Rockwood, and T. R. Jones. 2000. Adaptively Sampled Distance Fields: A General Representation of Shape for Computer Graphics. In Proc. of the 27th Annual Conference on Computer Graphics and Interactive Techniques (SIGGRAPH ’00). ACM Press/Addison-Wesley Publishing Co., USA, 249–254.
- M. Geilinger, D. Hahn, J. Zehnder, M. Bächer, B. Thomaszewski, and S. Coros. 2020. ADD: Analytically Differentiable Dynamics for Multi-Body Systems with Frictional Contact. ACM Trans. Graph. 39, 6, Article 190 (Nov. 2020), 15 pages.
- E. G. Gilbert, D. W. Johnson, and S. S. Keerthi. 1988. A fast procedure for computing the distance between complex objects in three-dimensional space. IEEE Journal on Robotics and Automation 4, 2 (1988), 193–203.
- H. Goldstein, C. Poole, and J. Safko. 2002. Classical mechanics. Addison-Wesley, USA. 638 pages.
- S. Goyal, A. Ruina, and J. Papadopoulos. 1989. Limit Surface and Moment Funktion Descriptions of Planar Sliding. In Proc. of the 1989 IEEE Intl. Conference on Robotics and Automation (Vol. 2). IEEE, Scottsdale, AZ, 794–799.
- D. Harmon, E. Vouga, B. Smith, R. Tamstorf, and E. Grinspun. 2009. Asynchronous Contact Mechanics. ACM Trans. Graph. 28, 3, Article 87, 12 pages.
- D. Harmon, E. Vouga, R. Tamstorf, and E. Grinspun. 2008. Robust Treatment of Simultaneous Collisions. ACM Trans. Graph. 27, 3 (aug 2008), 1–4.
- S. Hasegawa, N. Fujii, Y. Koike, and M. Sato. 2003. Real-Time Rigid Body Simulation Based on Volumetric Penalty Method. In HAPTICS ’03: Proc. of the 11th Symposium on Haptic Interfaces for Virtual Environment and Teleoperator Systems. IEEE Computer Society, Los Alamitos, CA, USA, 326.
- J. Jansson and J. S. M. Vergeest. 2002. A discrete mechanics model for deformable bodies. Computer-Aided Design 34, 12 (2002), 913–928.
- J. Jansson and J. S. M. Vergeest. 2003. Combining Deformable- and Rigid-Body Mechanics Simulation. Vis. Comput. 19, 5 (Aug. 2003), 280–290.
- M. Jean. 1999. The non-smooth contact dynamics method. Computer Methods in Applied Mechanics and Engineering 177, 3–4 (July 1999), 235–257.
- M. W. Jones, J. A. Baerentzen, and M. Sramek. 2006. 3D distance fields: A survey of techniques and applications. IEEE Transactions on visualization and Computer Graphics 12, 4 (2006), 581–599.
- F. Jourdan, P. Alart, and M. Jean. 1998. A Gauss-Seidel like algorithm to solve frictional contact problems. Computer Methods in Applied Mechanics and Engineering 155, 1 (1998), 31 — 47.
- J. J. Júdice and F. M. Pires. 1994. A block principal pivoting algorithm for large-scale strictly monotone linear complementarity problems. Computers & operations research 21, 5 (1994), 587–596.
- C. Kane, E. A. Repetto, M. Ortiz, and J. E. Marsden. 1999. Finite element analysis of nonsmooth contact. CMAME 180, 1–2 (1999).
- D. M. Kaufman, S. Sueda, D. L. James, and D. K. Pai. 2008. Staggered Projections for Frictional Contact in Multibody Systems. ACM Trans. Graph. 27, 5, Article Article 164 (Dec. 2008), 11 pages.
- T. Kim and D. Eberle. 2020. Dynamic Deformables: Implementation and Production Practicalities. In ACM SIGGRAPH 2020 Courses (Virtual Event, USA) (SIGGRAPH ’20). ACM, New York, NY, USA, Article 23, 182 pages.
- Y. J. Kim, M. A. Otaduy, M. C. Lin, and D. Manocha. 2002. Fast Penetration Depth Computation for Physically-Based Animation. In Proc. of the 2002 ACM SIGGRAPH/Eurographics Symposium on Computer Animation (San Antonio, Texas) (SCA ’02). ACM, New York, NY, USA, 23–31.
- D. Koschier, C. Deul, and J. Bender. 2016. Hierarchical Hp-Adaptive Signed Distance Fields. In Proc. of the 2016 ACM SIGGRAPH/Eurographics Symposium on Computer Animation (Zurich, Switzerland) (SCA ’16). Eurographics Association, Goslar, DEU, 189–198.
- C. Lacoursiere and M. Linde. 2011. Spook: a variational time-stepping scheme for rigid multibody systems subject to dry frictional contacts. Technical Report. HPC2N and Department of Computer Science, Umeaa University, Sweeden.
- L. Lan, D. M. Kaufman, M. Li, C. Jiang, and Y. Yang. 2022. Affine Body Dynamics: Fast, Stable & Intersection-free Simulation of Stiff Materials. ACM Trans. Graph. (SIGGRAPH) 41, 4, Article 67 (2022).
- L. Lan, Y. Yang, D. Kaufman, J. Yao, M. Li, and C. Jiang. 2021. Medial IPC: Accelerated Incremental Potential Contact with Medial Elastics. ACM Trans. Graph. (SIGGRAPH) 40, 4, Article 158 (July 2021), 16 pages.
- R. I. Leine and C. Glocker. 2003. A set-valued force law for spatial coulomb-contensou friction. European Journal of Mechanics – A/Solids 22, 2 (2003), 193–216.
- M. Li, Z. Ferguson, T. Schneider, T. Langlois, D. Zorin, D. Panozzo, C. Jiang, and D. M. Kaufman. 2020. Incremental Potential Contact: Intersection- and Inversion-free Large Deformation Dynamics. ACM Trans. Graph. (SIGGRAPH) 39, 4 (2020).
- M. Li, D. M. Kaufman, and C. Jiang. 2021. Codimensional Incremental Potential Contact. ACM Trans. Graph. (SIGGRAPH) 40, 4, Article 170 (July 2021), 24 pages.
- X. Li, Y. Fang, M. Li, and C. Jiang. 2022a. BFEMP: Interpenetration-free MPM-FEM coupling with barrier contact. Computer Methods in Applied Mechanics and Engineering 390 (2022), 114350.
- X. Li, M. Li, and C. Jiang. 2022b. Energetically Consistent Inelasticity for Optimization Time Integration. ACM Trans. Graph. (SIGGRAPH) 41, 4, Article 52 (2022).
- J. Lloyd. 2005. Fast Implementation of Lemke’s Algorithm for Rigid Body Contact Simulation. In ICRA ’05: Proc. of the 2005 IEEE Intl. Conference on Robotics and Automation. IEEE, Barcelona, Spain, 4538–4543.
- P. Lötstedt. 1984. Numerical Simulation of Time-Dependent Contact and Friction Problems in Rigid Body Mechanics. SIAM journal on scientific and statistical computing 5, 2 (1984), 370–393.
- M. Macklin, K. Erleben, M. Müller, N. Chentanez, S. Jeschke, and Z. Corse. 2020a. Local Optimization for Robust Signed Distance Field Collision. Proc. of the ACM on Computer Graphics and Interactive Techniques 3, 1 (2020), 1–17.
- M. Macklin, K. Erleben, M. Müller, N. Chentanez, S. Jeschke, and T. Y. Kim. 2020b. Primal/Dual Descent Methods for Dynamics. In Proc. of the 2020 ACM SIGGRAPH/Eurographics Symposium on Computer Animation (Virtual Event, Canada) (SCA ’20). Eurographics Association, Goslar, DEU, Article 9, 12 pages.
- M. Macklin, K. Erleben, M. Müller, N. Chentanez, S. Jeschke, and V. Makoviychuk. 2019. Non-Smooth Newton Methods for Deformable Multi-Body Dynamics. ACM Trans. Graph. 38, 5, Article Article 140 (Oct. 2019), 20 pages.
- H. Mazhar, T. Heyn, D. Negrut, and A. Tasora. 2015. Using Nesterov’s Method to Accelerate Multibody Dynamics with Friction and Contact. ACM Trans. Graph. 34, 3, Article 32 (May 2015), 14 pages.
- M. McKenna and D. Zeltzer. 1990. Dynamic simulation of autonomous legged locomotion. In Proc. of the 17th Annual Conference on Computer Graphics and Interactive Techniques (SIGGRAPH ’90). ACM, Dallas, TX, USA, 29–38.
- X. Merlhiot. 2007. A robust, efficient and time-stepping compatible collision detection method for non-smooth contact between rigid bodies of arbitrary shape. In ECCOMAS ’07: Proc. of the 2007 Multibody Dynamics ECCOMAS Thematic Conference. ECCOMAS, Milano, Italy, 20.
- M. Moore and J. Wilhelms. 1988. Collision detection and response for computer animationr3. In Proc. of the 15th annual conference on Computer graphics and interactive techniques (SIGGRAPH ’88). ACM, New York, NY, USA, 289–298.
- J. J. Moreau. 1999. Numerical aspects of the sweeping process. Computer Methods in Applied Mechanics and Engineering 177, 3–4 (July 1999), 329–349.
- M. Müller, N. Chentanez, T.-Y. Kim, and M. Macklin. 2015. Air Meshes for Robust Collision Handling. ACM Trans. Graph. (SIGGRAPH) 34, 4, Article 133 (July 2015).
- T. S. Munson, F. Facchinei, M. C. Ferris, A. Fischer, and C. Kanzow. 2001. The Semismooth Algorithm for Large Scale Complementarity Problems. INFORMS Journal on Computing 13, 4 (2001), 294–311.
- K. G. Murty. 1974. Note on a Bard-type scheme for solving the complementarity problem. Opsearch 11, 2–3 (1974), 123–130.
- K. G. Murty and F.-T. Yu. 1988. Linear Complementarity, Linear and Nonlinear Programming. Vol. 3. Helderman-Verlag, Berlin, Germany. 629 pages.
- R. Narain, M. Overby, and G. E. Brown. 2016. ADMM ⊇ Projective Dynamics: Fast Simulation of General Constitutive Models. In Proc. of the 2016 ACM SIGGRAPH/Eurographics Symposium on Computer Animation (Zurich, Switzerland) (SCA ’16). Eurographics Association, 21–28.
- X. Ni, L. V. Kale, and R. Tamstorf. 2015. Scalable Asynchronous Contact Mechanics Using Charm++. In 2015 IEEE International Parallel and Distributed Processing Symposium. 677–686.
- S. M. Niebe. 2014. Rigid Bodies in Contact: and Everything in Between. Ph.D. Dissertation. Department of Computer Science, Faculty of Science, University of Copenhagen.
- J. Nocedal and S. J. Wright. 2006. Numerical optimization. Springer-Verlag, New York. 664 pages.
- M. Otaduy, R. Tamstorf, D. Steinemann, and M. Gross. 2009a. Implicit Contact Handling for Deformable Objects. Comp. Graph. Forum 28 (04 2009).
- M. A. Otaduy, R. Tamstorf, D. Steinemann, and M. Gross. 2009b. Implicit Contact Handling for Deformable Objects. Comp. Graph. Forum (Proc. of Eurographics) 28, 2 (apr 2009). http://www.gmrv.es/Publications/2009/OTSG09
- S. Pabst, B. Thomaszewski, and W. Straßer. 2009. Anisotropic Friction for Deformable Surfaces and Solids. In Proc. of the 2009 ACM SIGGRAPH/Eurographics Symposium on Computer Animation (New Orleans, Louisiana) (SCA ’09). ACM, New York, NY, USA, 149–154.
- N. Parikh and S. Boyd. 2014. Proximal Algorithms. Found. Trends Optim. 1, 3 (Jan. 2014), 127–239.
- A. Peiret, S. Andrews, J. Kovecses, P. G. Kry, and M. Teichmann. 2019. Schur Complement-based Substructuring of Stiff Multibody Systems with Contact. ACM Trans. Graph. 38, 5, Article 150 (2019), 17 pages.
- M. Poulsen, S. Niebe, and K. Erleben. 2010. Heuristic Convergence Rate Improvements of the Projected Gauss-Seidel Method for Frictional Contact Problems. In WSCG ’10: In Proc. of the 18th Intl. Conf. in Central Europe on Computer Graphics, Visualization and Computer Vision. University of West Bohemia, Plzen, Czech Republic, 135–142.
- S. Redon, A. Kheddar, and S. Coquillart. 2002. Fast Continuous Collision Detection between Rigid Bodies. Computer Graphics Forum 21 (May 2002).
- T. Schneider, J. Dumas, X. Gao, D. Zorin, and D. Panozzo. 2019. Polyfem.
- G. Sheng Chen and X. Liu. 2016. Chapter 3 – Friction. In Friction Dynamics, Gang Sheng Chen and Xiandong Liu (Eds.). Woodhead Publishing, Cambridge, UK, 91–159.
- E. Sifakis and J. Barbic. 2012. FEM Simulation of 3D Deformable Solids: A Practitioner’s Guide to Theory, Discretization and Model Reduction. In ACM SIGGRAPH 2012 Courses (Los Angeles, California) (SIGGRAPH ’12). ACM, New York, NY, USA, Article 20, 50 pages.
- M. Silcowitz, S. Niebe, and K. Erleben. 2009. Nonsmooth Newton Method for Fischer Function Reformulation of Contact Force Problems for Interactive Rigid Body Simulation. In Proc. of the 6th Workshop on Virtual Reality Interaction and Physical Simulation (Karlsruhe, DE) (VRIPHYS ’09). The Eurographics Association, Karlsruhe, DE, 105–114.
- M. Silcowitz, S. Niebe, and K. Erleben. 2010a. A nonsmooth nonlinear conjugate gradient method for interactive contact force problems. The Visual Computer 26, 6 (2010), 893–901.
- M. Silcowitz, S. Niebe, and K. Erleben. 2010b. Projected Gauss-Seidel Subspace Minimization Method for Interactive Rigid Body Dynamics. In VISIGRAPP ’10: Proc. of the 5th Intl. Conference on Computer Graphics Theory and Applications. Springer Berlin Heidelberg, Angers, France, 218–229.
- M. Silcowitz-Hansen. 2010. Jinngine: a Physics Engine Written In Java. https://github.com/rzel/jinngine
- J. M. Snyder. 1992. Interval Analysis for Computer Graphics. In Proceedings of the 19th Annual Conference on Computer Graphics and Interactive Techniques (SIGGRAPH ’92). Association for Computing Machinery, New York, NY, USA, 121–130.
- D. E. Stewart and J. C. Trinkle. 1996. An Implicit Time-Stepping Scheme for Rigid Body Dynamics with Inelastic Collisions and Coulomb Friction. Intl. Journal of Numerical Methods in Engineering 39, 15 (1996), 2673–2691.
- C. W. Studer. 2008. Augmented Time-stepping Integration of Non-smooth Dynamical Systems. Ph.D. Dissertation. ETH Zurich.
- I. E. Sutherland and G. W. Hodgman. 1974. Reentrant polygon clipping. Commun. ACM 17, 1 (1974), 32–42.
- M. Tang, R. Tong, Z. Wang, and D. Manocha. 2014. Fast and Exact Continuous Collision Detection with Bernstein Sign Classification. ACM Trans. Graph. 33 (Nov. 2014), 186:1–186:8. Issue 6.
- A. Tasora, D. Mangoni, S. Benatti, and R. Garziera. 2021. Solving variational inequalities and cone complementarity problems in nonsmooth dynamics using the alternating direction method of multipliers. Intl. Journal for Numerical Methods in Engineering 122, 16 (2021).
- J. Teran, E. Sifakis, G. Irving, and R. Fedkiw. 2005. Robust Quasistatic Finite Elements and Flesh Simulation. In Proceedings of the 2005 ACM SIGGRAPH/Eurographics Symposium on Computer Animation (Los Angeles, California) (SCA ’05). Association for Computing Machinery, New York, NY, USA, 181–190.
- D. Terzopoulos, J. Platt, A. Barr, and K. Fleischer. 1987. Elastically Deformable Models. In Proc. of the 14th Annual Conference on Computer Graphics and Interactive Techniques (SIGGRAPH ’87). Association for Computing Machinery, New York, NY, USA, 205–214.
- E. Todorov, T. Erez, and Y. Tassa. 2012. MuJoCo: A physics engine for model-based control. In 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems. 5026–5033.
- G. Van Den Bergen. 2003. Collision detection in interactive 3D environments. CRC Press, San Francisco, USA. 277 pages.
- M. Verschoor and A. C. Jalba. 2019. Efficient and accurate collision response for elastically deformable models. ACM Trans. Graph. 38, 2 (2019), 1–20.
- B. Wang, Z. Ferguson, X. Jiang, M. Attene, D. Panozzo, and T. Schneider. 2022. Fast and Exact Root Parity for Continuous Collision Detection. Computer Graphics Forum (Proceedings of Eurographics) 41, 2 (2022), 9.
- B. Wang, Z. Ferguson, T. Schneider, X. Jiang, M. Attene, and D. Panozzo. 2021. A Large-Scale Benchmark and an Inclusion-Based Algorithm for Continuous Collision Detection. ACM Trans. Graph. 40, 5, Article 188 (sep 2021), 16 pages.
- H. Wang. 2015. A Chebyshev Semi-iterative Approach for Accelerating Projective and Position-based Dynamics. ACM Trans. Graph. 34, 6 (Oct. 2015), 246:1–246:9.
- H. Xu and J. Barbič. 2014. Signed distance fields for polygon soup meshes. In Proc. of the 40th Graphics Interface Conference (GI ’14). Canadian Information Processing Society, Montreal, Canada, 35–41.
- H. Xu, Y. Zhao, and J. Barbič. 2014. Implicit Multibody Penalty-based Distributed Contact. IEEE Transactions on Visualization and Computer Graphics 20, 9 (Sep. 2014), 1266–1279.
- Y. Zhao, J. Choo, Y. Jiang, M. Li, C. Jiang, and K. Soga. 2022. A barrier method for frictional contact on embedded interfaces. Computer Methods in Applied Mechanics and Engineering 393 (2022), 114820.