“Computing self-supporting surfaces by regular triangulation” by Liu, Pan, Snyder, Wang and Guo
Conference:
Type(s):
Title:
- Computing self-supporting surfaces by regular triangulation
Session/Category Title: Building Structures & Layouts
Presenter(s)/Author(s):
Moderator(s):
Abstract:
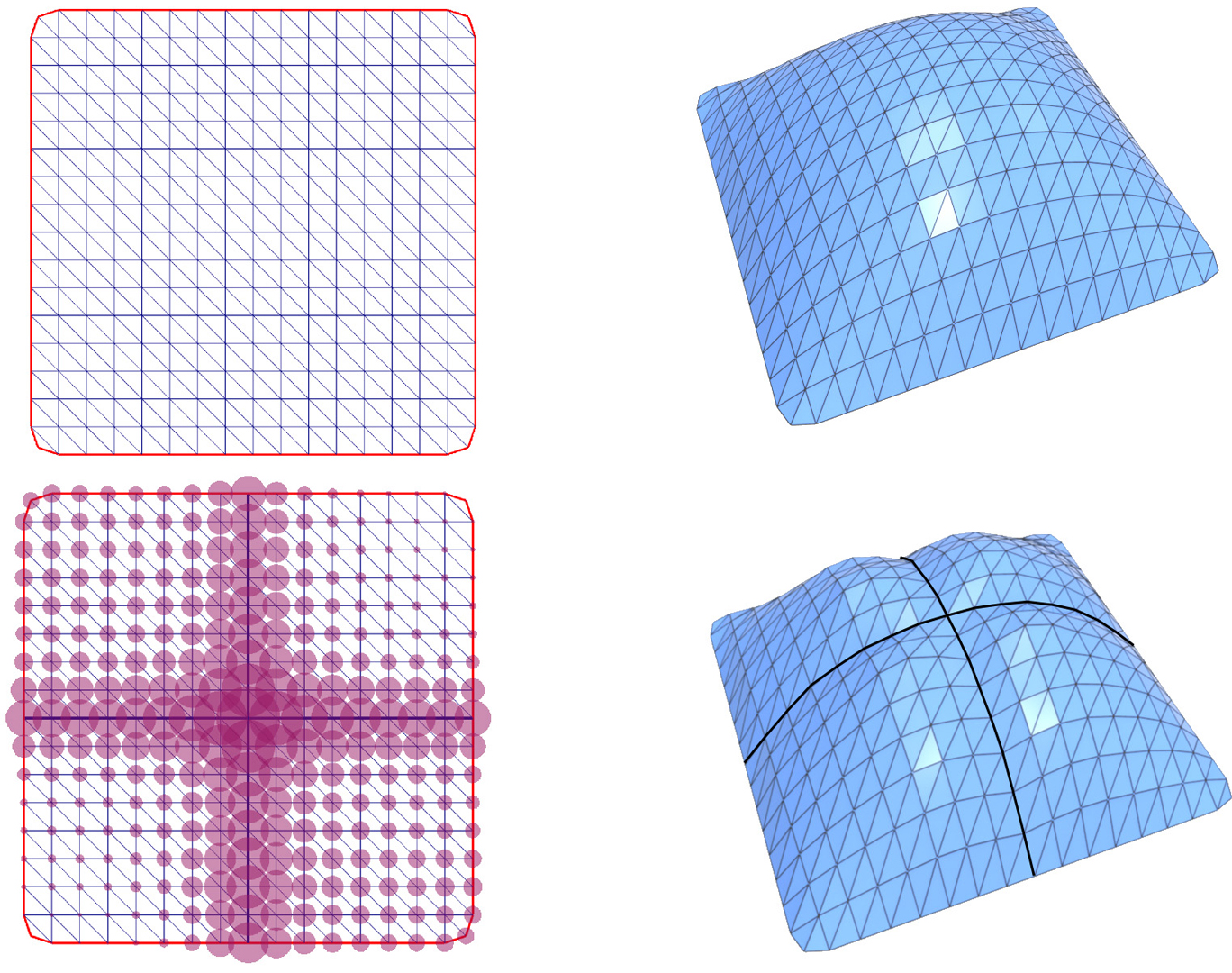
Masonry structures must be compressively self-supporting; designing such surfaces forms an important topic in architecture as well as a challenging problem in geometric modeling. Under certain conditions, a surjective mapping exists between a power diagram, defined by a set of 2D vertices and associated weights, and the reciprocal diagram that characterizes the force diagram of a discrete self-supporting network. This observation lets us define a new and convenient parameterization for the space of self-supporting networks. Based on it and the discrete geometry of this design space, we present novel geometry processing methods including surface smoothing and remeshing which significantly reduce the magnitude of force densities and homogenize their distribution.
References:
1. Alliez, P., Cohen-Steiner, D., Yvinec, M., and Desbrun, M. 2005. Variational tetrahedral meshing. ACM Trans. Graph. (SIGGRAPH) 24, 3, 617–625. Google ScholarDigital Library
2. Aurenhammer, F. 1987. Power diagrams: properties, algorithms and applications. SIAM J. Comput. 16, 1, 78–96. Google ScholarDigital Library
3. Aurenhammer, F. 1987. A criterion for the affine equivalence of cell complexes in Rd and convex polyhedra in Rd+1. Discrete Comp. Geom. 2, 49–64.Google ScholarDigital Library
4. Block, P., and Lachauer, L. 2011. Closest-Fit, Compression-only solutions for freeform shells. In Proc. of the IABSE-IASS Symp.Google Scholar
5. Block, P., and Ochsendorf, J. 2007. Thrust Network Analysis: a new methodology for three-dimensional equilibrium. J. Int. Assoc. Shell and Spatial Structures 48, 167–173.Google Scholar
6. Block, P. 2009. Thrust Network Analysis: Exploring Three-dimensional Equilibrium. PhD thesis, Massachusetts Institute of Technology.Google Scholar
7. CGAL, Computational Geometry Algorithms Library. http://www.cgal.org.Google Scholar
8. Chen, L., and Xu, J. 2004. Optimal Delaunay triangulations. J. Comput. Math. 22, 299–308.Google Scholar
9. Cheng, S.-W., and Dey, T. K. 2004. Quality meshing with weighted Delaunay refinement. SIAM J. Comput. 33, 1, 69–93. Google ScholarDigital Library
10. Cremona, L. 1890. Graphical Statics. Oxford University Press.Google Scholar
11. de Goes, F., Breeden, K., Ostromoukhov, V., and Desbrun, M. 2012. Blue noise through optimal transport. ACM Trans. Graph. (SIGGRAPH ASIA) 31, 6, 171:1–171:11. Google ScholarDigital Library
12. Du, Q., Faber, V., and Gunzburger, M. 1999. Centroidal Voronoi tessellations: applications and algorithms. SIAM Rev. 41, 637–676. Google ScholarDigital Library
13. Fraternali, F., Angelillo, M., and Fortunato, A. 2002. A lumped stress method for plane elastic problems and the discrete-continuum approximation. J. Int. Solids and Structures 39, 6211–6240.Google ScholarCross Ref
14. Fraternali, F. 2010. A thrust network approach to the equilibrium problem of unreinforced masonry vaults via polyhedral stress functions. Mechanics Research Communications 37, 198–204.Google ScholarCross Ref
15. Gertz, E. M., and Wright, S. J. 2003. Object-oriented software for quadratic programming. ACM Trans. Math. Softw. 29, 58–81. Google ScholarDigital Library
16. Glickenstein, D. 2005. Geometric triangulations and discrete Laplacians on manifolds. arXiv:0508188 {math.MG}.Google Scholar
17. Heyman, J. 1966. The stone skeleton. J. Int. Solids and Structures 2, 249–279.Google ScholarCross Ref
18. Heyman, J. 1997. The Stone Skeleton: Structural Engineering of Masonry Architecture. Cambridge University Press.Google Scholar
19. Kilian, A., and Ochsendorf, J. 2005. Paticle-spring systems for structural form finding. J. Int. Assoc. Shell and Spatial Structures 46, 77–84.Google Scholar
20. Kilian, A. 2006. Design Exploration through Bidirectional Modeling of Constraints. PhD thesis, Massachusetts Institute of Technology. Google ScholarDigital Library
21. Lawson, C. 1977. Software for C1 surface interpolation. In Mathematical Software III, Academic Press, New York, 161–194.Google Scholar
22. Liu, Y., Wang, W., Lévy, B., Sun, F., Yan, D.-M., Lu, L., and Yang, C. 2009. On centroidal Voronoi tessellation — energy smoothness and fast computation. ACM Trans. Graph. 28, 101:1–101:17. Google ScholarDigital Library
23. Maxwell, J. C. 1869. On reciprocal diagrams, frames and diagrams of forces. Transactions of the Royal Society of Edinburgh 26, 1–40.Google ScholarCross Ref
24. Mullen, P., Memari, P., de Goes, F., and Desbrun, M. 2011. HOT: Hodge-optimized triangulations. ACM Trans. Graph. (SIGGRAPH) 30, 4, 103:1–103:12. Google ScholarDigital Library
25. ODwyer, D. 1999. Funicular analysis of masonry vaults. Computers & Structures 73, 187–197.Google ScholarCross Ref
26. Rippmann, M., Lachauer, L., and Block, P. 2012. Interactive vault design. J. Int. Space Structures 27, 219–230.Google ScholarCross Ref
27. Schek, H.-J. 1974. The force density method for form finding and computation of general networks. Comput. Methods in Applied Mech. and Eng. 3, 115–134.Google ScholarCross Ref
28. Schiftner, A., and Balzer, J. 2010. Statics-sensitive layout of planar quadrilateral meshes. In Advances in Architectural Geometry, 221–236.Google Scholar
29. Smith, J., Hodgins, J., Oppenheim, I., and Witkin, A. 2002. Creating models of truss structures with optimization. ACM Trans. Graph. (SIGGRAPH) 21, 3, 295–301. Google ScholarDigital Library
30. Umetani, N., Igarashi, T., and Mitra, N. J. 2012. Guided exploration of physically valid shapes for furniture design. ACM Trans. Graph. (SIGGRAPH) 31, 4, 86:1–86:11. Google ScholarDigital Library
31. Vouga, E., Höbinger, M., Wallner, J., and Pottmann, H. 2012. Design of self-supporting surfaces. ACM Trans. Graph. (SIGGRAPH) 31, 4, 87:1–87:11. Google ScholarDigital Library
32. Wardetzky, M., Mathur, S., Kälberer, F., and Grinspun, E. 2007. Discrete Laplace operators: no free lunch. In Symp. on Geom. Proc. Google ScholarDigital Library
33. Whiting, E., Ochsendorf, J., and Durand, F. 2009. Procedural modeling of structurally-sound masonry buildings. ACM Trans. Graph. (SIGGRAPH ASIA) 28, 112:1–112:9. Google ScholarDigital Library
34. Whiting, E., Shin, H., Wang, R., Ochsendorf, J., and Durand, F. 2012. Structural optimization of 3D masonry buildings. ACM Trans. Graph. (SIGGRAPH ASIA) 31, 159:1–159:11. Google ScholarDigital Library
35. Zorin, D., Schröder, P., and Sweldens, W. 1996. Interpolating subdivision for meshes with arbitrary topology. In SIGGRAPH ’96, 189–192. Google ScholarDigital Library