“Computing geometry-aware handle and tunnel loops in 3D models” by Dey, Li, Sun and Cohen-Steiner

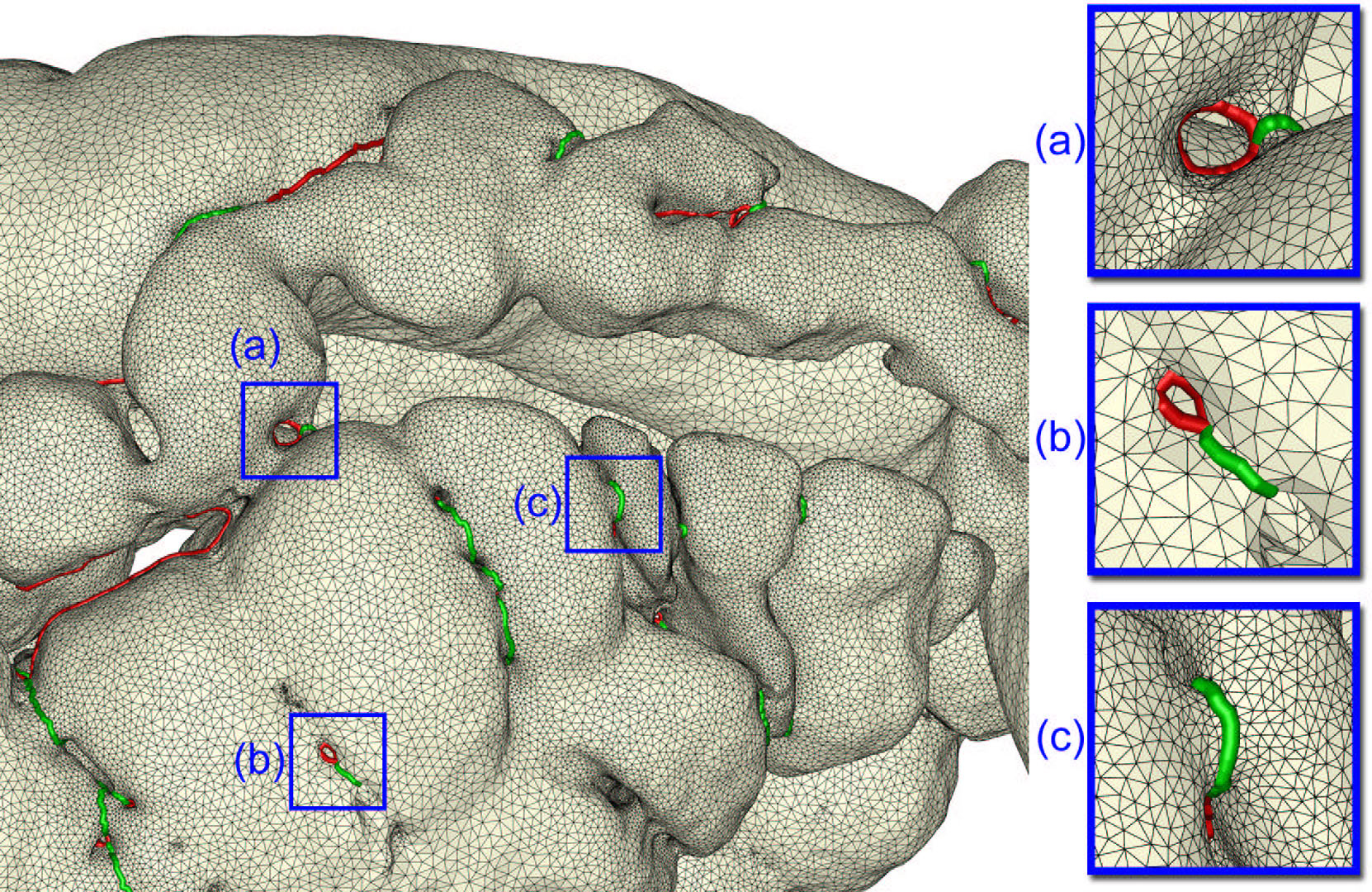
Many applications such as topology repair, model editing, surface parameterization, and feature recognition benefit from computing loops on surfaces that wrap around their ‘handles’ and ‘tunnels’. Computing such loops while optimizing their geometric lengths is difficult. On the other hand, computing such loops without considering geometry is easy but may not be very useful. In this paper we strike a balance by computing topologically correct loops that are also geometrically relevant. Our algorithm is a novel application of the concepts from topological persistence introduced recently in computational topology. The usability of the computed loops is demonstrated with some examples in feature identification and topology simplification.

1. Alliez, P., Cohen-Steiner, D., Yvinec, M., and Desbrun, M. 2005. Variational tetrahedral meshing. In Proc. SIGGRAPH 2005, 617–625. Google ScholarDigital Library
2. Ben-Chen, M., Gotsman, C., and Bunin, G. 2008. Conformal flattening by curvature prescription and metric scaling. Computer Graphics Forum (Proc. Eurographics) 27.Google Scholar
3. Biasotti, S., Giorgi, D., Spagnuolo, M., and Falcidieno, B. 2008. Reeb graphs for shape analysis and applications. Theoretical Comput. Sci. 392, 5–22. Google ScholarDigital Library
4. Bischoff, S., and Kobbelt, L. 2005. Structure preserving CAD model repair. Comput. Graphics Forum 24, 527–536.Google ScholarCross Ref
5. Chen, C., and Freedman, D. 2008. Quantifying homology classes. In Sympos. Theoretical Aspects Comput. Sci., 169–180.Google Scholar
6. Cheng, S.-W., Dey, T. K., and Levine, J. A. 2007. A practical Delaunay meshing algorithm for a large class of domains. In Proc. 16th Internat. Meshing Roundtable, 477–494.Google Scholar
7. Cohen-Steiner, D., Edelsbrunner, H., and Morozov, D. 2006. Vines and vineyards by updating persistence in linear time. In Proc. 22nd Ann. Sympos. Comput. Geom., 119–126. Google ScholarDigital Library
8. Dey, T. K., and Sun, J. 2006. Defining and computing curve-skeletons with medial geodesic function. In Proc. Sympos. Geom. Processing, 143–152. Google ScholarDigital Library
9. Dey, T. K., Li, K., and Sun, J. 2007. On computing handle and tunnel loops. In IEEE Proc. Internat. Conf. Cyberworlds, 357–366. Google ScholarCross Ref
10. Dey, T. K. 2007. Curve and surface reconstruction: algorithms with mathematical analysis. Cambridge University Press. Google ScholarDigital Library
11. Edelsbrunner, H., Letscher, D., and Zomorodian, A. 2002. Topological persistence and simplification. Discrete Comput. Geom. 28, 511–533.Google ScholarDigital Library
12. El-Sana, J., and Varshney, A. 1997. Controlled simplification of genus for polygonal models. In Proc. IEEE Visualization, 403–412. Google ScholarDigital Library
13. Éric Colin de Verdière, and Erickson, J. 2006. Tightening non-simple paths and cycles on surfaces. In Proc. ACM-SIAM Sympos. Discrete Algorithms, 192–201. Google ScholarDigital Library
14. Éric Colin de Verdière, and Lazarus, F. 2005. Optimal system of loops on an orientable surface. Discrete Comput. Geom. 33, 507–534.Google ScholarDigital Library
15. Erickson, J., and Whittlesey, K. 2005. Greedy optimal homotopy and homology generators. In Proc. ACM-SIAM Sympos. Discrete Algorithms, 1038–1046. Google ScholarDigital Library
16. Gu, X., Gortler, S., and Hoppe, H. 2002. Geometry images. In Proc. SIGGRAPH 2002, 355–361. Google ScholarDigital Library
17. Guskov, I., and Wood, Z. 2001. Topological noise removal. In Proc. Graphics Interface 2001, 19–26. Google ScholarDigital Library
18. Hatcher, A. 2002. Algebraic Topology. Cambridge University Press.Google Scholar
19. Levoy, M., Pulli, K., Curless, B., Rusinkiewicz, S., Koller, D., Pereira, L., Ginzton, M., Anderson, S., Davis, J., Ginsberg, J., Shade, J., and Fulk, D. 2000. The digital Michelangelo project: 3d scanning of large statues. In Proc. SIGGRAPH 2000, 131–144. Google ScholarDigital Library
20. Ni, X., Garland, M., and Hart, J. C. 2004. Fair morse functions for extracting the topological structure of a surface mesh. In Proc. SIGGRAPH 2004, 613–622. Google ScholarDigital Library
21. Nooruddin, F. S., and Turk, G. 2003. Simplification and repair of polygonal models using volumetric techniques. IEEE Trans. Vis. Comput. Graph. 9, 191–205. Google ScholarDigital Library
22. Oudot, S., Rineau, L., and Yvinec, M. 2005. Meshing volumes bounded by smooth surfaces. In Proc. 14th Internat. Meshing Roundtable, 203–219.Google Scholar
23. Pascucci, V., Scorzelli, G., Bremer, P.-T., and Mascarenhas, A. 2007. Robust on-line computation of Reeb graphs: simplicity and speed. ACM Trans. Graphics. 58, 1–9. Google ScholarDigital Library
24. Shattuck, D. W., and Leahy, R. M. 2001. Automated graph-based analysis and correction of cortical volume topology. IEEE Trans. Med. Imaging 20, 1167–1177.Google ScholarCross Ref
25. Sheffer, A., and Hart, J. 2002. Seamster: inconspicuous low-distortion texture seam layout. In Proc. IEEE Visualization, 291–298. Google ScholarDigital Library
26. Wood, Z., Hoppe, H., Desbrun, M., and Schröder, P. 2004. Removing excess topology from isosurfaces. ACM Trans. Graphics 23, 511–533. Google ScholarDigital Library
27. Yin, X., Jin, M., and Gu, X. 2007. Computing shortest cycles using universal covering space. Visual Computer 23, 999–1004. Google ScholarDigital Library
28. Zhou, Q.-Y., Ju, T., and Hu, S.-M. 2007. Topology repair of solid models using skeletons. IEEE Trans. Vis. Comput. Graph. 13, 675–685. Google ScholarDigital Library
29. Zomorodian, A., and Carlsson, G. 2005. Computing persistent homology. Discrete Comput. Geom. 33, 249–274. Google ScholarDigital Library
30. Zomorodian, A., and Carlsson, G. 2007. Localized homology. In Proc. Shape Modeling Internat., 189–198. Google ScholarDigital Library