“Color image quantization for frame buffer display” by Heckbert

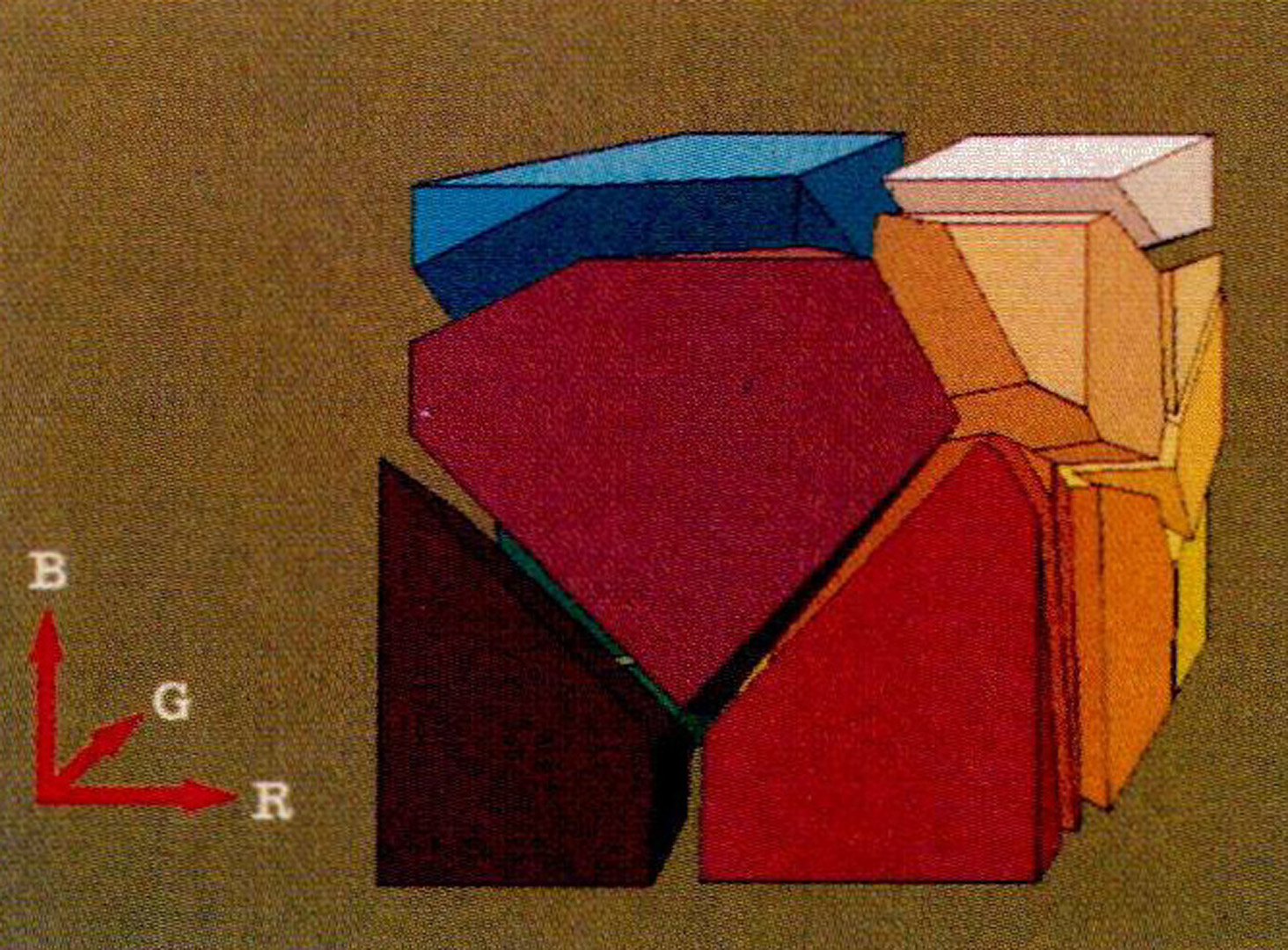
Algorithms for adaptive, tapered quantization of color images are described. The research is motivated by the desire to display high-quality reproductions of color images with small frame buffers. It is demonstrated that many color images which would normally require a frame buffer having 15 bits per pixel can be quantized to 8 or fewer bits per pixel with little subjective degradation. In most cases, the resulting images look significantly better than those made with uniform quantization. The color image quantization task is broken into four phases: 1) Sampling the original image for color statistics 2) Choosing a colormap based on the color statistics 3) Mapping original colors to their nearest neighbors in the colormap 4) Quantizing and redrawing the original image (with optional dither). Several algorithms for each of phases 2-4 are described, and images created by each given.

1. Bellman, R. Dynamic Programming. Princeton University Press, Princeton, 1957.
2. Bentley, J. L., Friedman, J. H. Data structures for range searching. Computing Surveys 11, 4 (Dec. 1979), 397-409.
3. Bruce, J. D. Optimum Quantization. MIT R.L.E. Technical Report #429, (1965).
4. Elias, P. Bounds on performance of optimum quantizers. IEEE Trans. on Information Theory IT-16, 2 (Mar. 1970) 172-184.
5. Floyd, R. W., Steinberg, L. An adaptive algorithm for spatial gray scale. SID 75, Int. Symp. Dig. Tech. Papers (1975), 36.
6. Friedman, J. J., Bentley, J. L., and Finkel, R. A. An algorithm for finding best matches in logarithmic expected time. ACM Trans. Math. Software 3, (Sept. 1977), 209-226.
7. Gray, R. M., Kieffer, J. C., and Linde, Y. Locally optimal block quantizer design. Information and Control 45 (1980) 178-198.
8. Heckbert, P. Color Image Quantization for Frame Buffer Display. B.S. thesis Architecture Machine Group, MIT, Cambridge, Mass., 1980.
9. Huang, T. S., Tretiak, O. J., Prasada, B. T., and Yamaguchi, Y. Design considerations in PCM transmission of low-resolution monochrome still pictures. Proc. IEEE 55, 3 (Mar. 1967), 331.
10. In der Smitten, F. J. Data-reducing source encoding of color picture signals based on chromaticity classes. Nachrichtentech. Z. 27, (1974), 176.
11. Jain, A. K., and Pratt, W. K. Color image quantization. National Tele-communications Conference 1972 Record, IEEE Pub. No. 72, CHO 601-5-NTC, (Dec. 1972).
12. Jarvis, J. F., Judice, N., and Ninke, W.H. A survey of techniques for the display of continuous tone pictures on bilevel displays. Computer Graphics and Image Processing 5, 1 (Mar. 1976), 13-40.
13. Knuth, D. E. The Art of Computer Programming, vol. 3, Sorting and Searching. Addison-Wesley, Reading, Mass., 1973.
14. Koontz, W. L. G., Narendra, P. M., and Fukunaga, K. A branch and bound clustering algorithm. IEEE Trans. Comput. C-24, 9 (Sept. 1975), 908-915.
15. Limb, J. O., Rubinstein, C. B., and Thompson, J. E. Digital coding of color video signals – a review. IEEE Trans. Commun. COM-25, 11 (Nov. 1977), 1349-1385.
16. Lloyd, S. P. Least squares quantization in PCM’s. Bell Telephone Labs Memo, Murray Hill, N.J., 1957.
17. Max, J. Quantizing for minimum distortion. IRE Trans. Information Theory IT-6, (Mar. 1960), 7.
18. Newman, W. M., and Sproull, R. F. Principles of Interactive Computer Graphics. MacGraw-Hill, New York, 1979.
19. Panter, P. F., and Dite, W. Quantization distortion in pulse-count modulation with nonuniform spacing of levels. Proc. IRE 39, 1 (Jan. 1951), 44.
20. Pratt, W. K. Digital Image Processing. John Wiley and Sons, New York, 1978.
21. Roberts, L. G. Picture coding using pseudo-random noise. IRE Trans. Information Theory IT-8, (Feb. 1962), 145.
22. Stenger, L. Quantization of TV chrominance signals considering the visibility of small color differences. IEEE Trans. Communications COM-25, 11 (Nov. 1977), 1393.