“Build-to-last: strength to weight 3D printed objects” by Lu, Sharf, Zhao, Wei, Fan, et al. …
Conference:
Type:
Session Title:
- Fabrication
Title:
- Build-to-last: strength to weight 3D printed objects
Moderator(s):
Presenter(s)/Author(s):
Abstract:
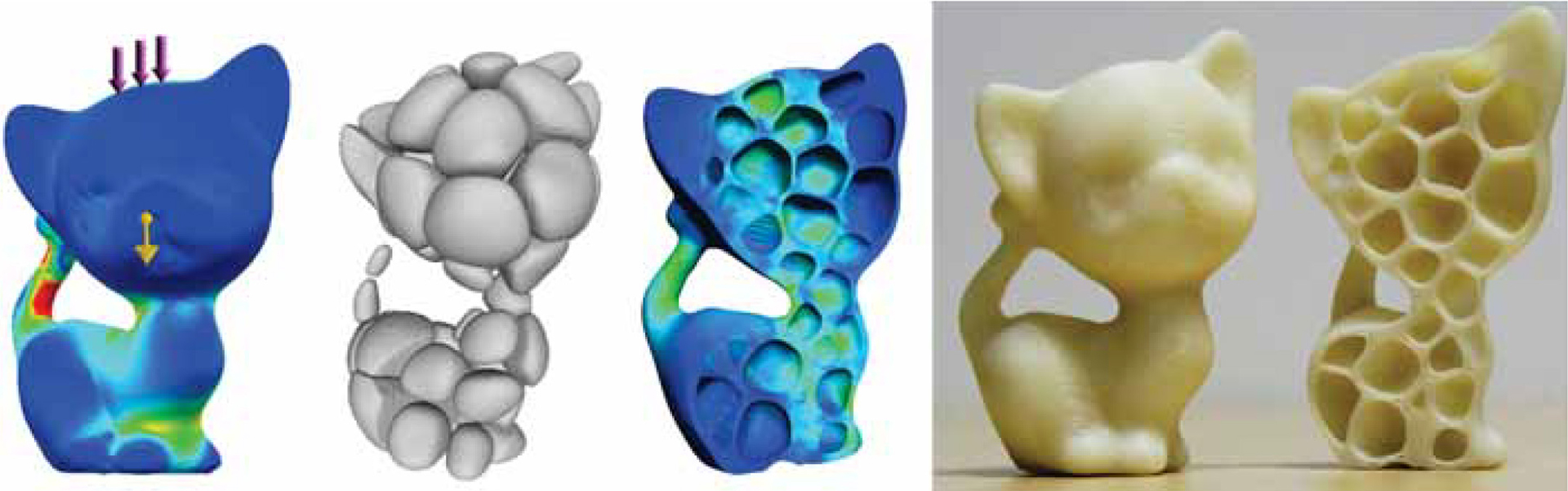
The emergence of low-cost 3D printers steers the investigation of new geometric problems that control the quality of the fabricated object. In this paper, we present a method to reduce the material cost and weight of a given object while providing a durable printed model that is resistant to impact and external forces.We introduce a hollowing optimization algorithm based on the concept of honeycomb-cells structure. Honeycombs structures are known to be of minimal material cost while providing strength in tension. We utilize the Voronoi diagram to compute irregular honeycomb-like volume tessellations which define the inner structure. We formulate our problem as a strength–to–weight optimization and cast it as mutually finding an optimal interior tessellation and its maximal hollowing subject to relieve the interior stress. Thus, our system allows to build-to-last 3D printed objects with large control over their strength-to-weight ratio and easily model various interior structures. We demonstrate our method on a collection of 3D objects from different categories. Furthermore, we evaluate our method by printing our hollowed models and measure their stress and weights.
References:
1. Bächer, M., Bickel, B., James, D. L., and Pfister, H. 2012. Fabricating articulated characters from skinned meshes. ACM Trans. Graph. 31, 4 (July), 47:1–47:9. Google ScholarDigital Library
2. Bickel, B., Bächer, M., Otaduy, M. A., Lee, H. R., Pfister, H., Gross, M. H., and Matusik, W. 2010. Design and fabrication of materials with desired deformation behavior. ACM Trans. Graph. 29, 4. Google ScholarDigital Library
3. Bickel, B., Kaufmann, P., Skouras, M., Thomaszewski, B., Bradley, D., Beeler, T., Jackson, P., Marschner, S., Matusik, W., and Gross, M. 2012. Physical face cloning. ACM Trans. Graph. 31, 4 (July), 118:1–118:10. Google ScholarDigital Library
4. Bronstein, A., Bronstein, M., and Kimmel, R. 2008. Numerical Geometry of Non-Rigid Shapes, 1 ed. Springer Publishing Company, Incorporated. Google ScholarDigital Library
5. Calì, J., Calian, D. A., Amati, C., Kleinberger, R., Steed, A., Kautz, J., and Weyrich, T. 2012. 3D-printing of non-assembly, articulated models. ACM Trans. Graph. 31, 6 (Nov.), 130:1–130:8. Google ScholarDigital Library
6. Ceylan, D., Li, W., Mitra, N. J., Agrawala, M., and Pauly, M. 2013. Designing and fabricating mechanical automata from mocap sequences. ACM Trans. Graph. 32, 6, 186. Google ScholarDigital Library
7. Chen, D., Levin, D. I. W., Didyk, P., Sitthi-Amorn, P., and Matusik, W. 2013. Spec2fab: A reducer-tuner model for translating specifications to 3D prints. ACM Trans. Graph. 32, 4, 135:1–135:10. Google ScholarDigital Library
8. Coros, S., Thomaszewski, B., Noris, G., Sueda, S., Forberg, M., Sumner, R. W., Matusik, W., and Bickel, B. 2013. Computational design of mechanical characters. ACM Trans. Graph. 32, 4 (July), 83:1–83:12. Google ScholarDigital Library
9. Crapo, H., and Whiteley, W. 1993. The geometry of rigid structures. Encyclopedia of Math., Cambridge University Press.Google Scholar
10. Crapo, H. 1979. Structural rigidity. Structural Topology 1, 26–45.Google Scholar
11. Du, Q., Faber, V., and Gunzburger, M. 1999. Centroidal voronoi tessellations: Applications and algorithms. SIAM Review 41, 4, 637–676. Google ScholarDigital Library
12. Haftka, R. T., and Grandhi, R. V. 1986. Structural shape optimization – a survey. Computer Methods in Applied Mechanics and Engineering 57, 1, 91–106. Google ScholarDigital Library
13. Hollister, S. 2005. Porous scaffold design for tissue engineering. Nat. Mater. 4, 7, 518–524.Google ScholarCross Ref
14. Khoda, A., Ozbolat, I. T., and Koc, B. 2013. Designing heterogeneous porous tissue scaffolds for additive manufacturing processes. Computer-Aided Design 45, 12, 1507–1523. Google ScholarDigital Library
15. Kindinger, J. 2001. Lightweight structural core. ASM Handbook 21, 180–183.Google Scholar
16. Kou, X., and Tan, S. 2010. A simple and effective geometric representation for irregular porous structure modeling. Computer-Aided Design 42, 10, 930–941. Google ScholarDigital Library
17. Li, X., Guo, X., Wang, H., He, Y., Gu, X., and Qin, H. 2007. Harmonic volumetric mapping for solid modeling applications. In Proceedings of the 2007 ACM Symposium on Solid and Physical Modeling, ACM, New York, NY, USA, SPM ’07, 109–120. Google ScholarDigital Library
18. Li, H., Vouga, E., Gudym, A., Luo, L., Barron, J. T., and Gusev, G. 2013. 3D self-portraits. ACM Trans. Graph. 32, 6 (November). Google ScholarDigital Library
19. Lloyd, S. P. 1982. Least squares quantization in PCM. IEEE Transactions on Information Theory 28, 2, 129–136. Google ScholarDigital Library
20. Patzak, B., and Rypl, D. 2012. Object-oriented, parallel finite element framework with dynamic load balancing. Adv. Eng. Softw., 35–50. Google ScholarDigital Library
21. Pottmann, H. 2012. Freeform architecture and fabrication-aware design. Computers & Graphics 36, 5 (Aug.). Google ScholarDigital Library
22. Prévost, R., Whiting, E., Lefebvre, S., and Sorkine-Hornung, O. 2013. Make it stand: balancing shapes for 3D fabrication. ACM Trans. Graph. 32, 4 (July), 81:1–81:10. Google ScholarDigital Library
23. Rivers, A., Moyer, I. E., and Durand, F. 2012. Position-correcting tools for 2d digital fabrication. ACM Trans. Graph. 31, 4 (July), 88:1–88:7. Google ScholarDigital Library
24. Rosenberg, I. 1980. Structural rigidity i: Foundations and rigidity criteria. In Combinatorics 79 Part I, M. Deza and I. Rosenberg, Eds., vol. 8 of Annals of Discrete Mathematics. Elsevier, 143–161.Google Scholar
25. Schroeder, C., Regli, W. C., Shokoufandeh, A., and Sun, W. 2005. Computer-aided design of porous artifacts. Computer-Aided Design 37, 3, 339–353.Google ScholarCross Ref
26. Si, H., 2007. Tetgen. a quality tetrahedral mesh generator.Google Scholar
27. Skouras, M., Thomaszewski, B., Bickel, B., and Gross, M. 2012. Computational design of rubber balloons. Comp. Graph. Forum 31, 2pt4 (May), 835–844. Google ScholarDigital Library
28. Skouras, M., Thomaszewski, B., Coros, S., Bickel, B., and Gross, M. 2013. Computational design of actuated deformable characters. ACM Trans. Graph. 32, 4 (July), 82:1–82:10. Google ScholarDigital Library
29. Stava, O., Vanek, J., Benes, B., Carr, N., and Měch, R. 2012. Stress relief: improving structural strength of 3D printable objects. ACM Trans. Graph. 31, 4 (July), 48:1–48:11. Google ScholarDigital Library
30. Telea, A., and Jalba, A. 2011. Voxel-based assessment of printability of 3D shapes. In Proceedings of the 10th international conference on Mathematical morphology and its applications to image and signal processing, Springer-Verlag, ISMM’11, 393–404. Google ScholarDigital Library
31. Umetani, N., and Schmidt, R. 2013. Cross-sectional structural analysis for 3d printing optimization. In SIGGRAPH Asia 2013 Technical Briefs, ACM, New York, NY, USA, SA ’13, 5:1–5:4. Google ScholarDigital Library
32. Vidimče, K., Wang, S.-P., Ragan-Kelley, J., and Matusik, W. 2013. Openfab: a programmable pipeline for multi-material fabrication. ACM Trans. Graph. 32, 4 (July), 136:1–136:12. Google ScholarDigital Library
33. Voronoi, G. 1908. Nouvelles applications des paramètres continus à la théorie des formes quadratiques. deuxième mémoire. recherches sur les p arallélloèdres primitifs. Journal für die reine und angewandte Mathematik (Crelles Journal) 1908, 134 (Jan.), 198–287.Google Scholar
34. Wang, W., Wang, T. Y., Yang, Z., Liu, L., Tong, X., Tong, W., Deng, J., Chen, F., and Liu, X. 2013. Cost-effective printing of 3D objects with skin-frame structures. ACM Trans. Graph. 32, 5. Google ScholarDigital Library
35. Wicke, M., Botsch, M., and Gross, M. 2007. A finite element method on convex polyhedra. Comp. Graph. Forum 26, 3, 355–364.Google ScholarCross Ref
36. Wilson, S. 1990. A new face of aerospace honeycomb. Materials & Design 11, 6, 323–326.Google ScholarCross Ref
37. Yan, D.-M., Wang, W., Lévy, B., and Liu, Y. 2013. Efficient computation of clipped voronoi diagram for mesh generation. Computer-Aided Design 45, 4, 843–852. Geometric Modeling and Processing 2010. Google ScholarDigital Library
38. Zhou, Q., Panetta, J., and Zorin, D. 2013. Worst-case structural analysis. ACM Trans. Graph. 32, 4 (July), 137:1–137:12. Google ScholarDigital Library
39. Zhu, L., Xu, W., Snyder, J., Liu, Y., Wang, G., and Guo, B. 2012. Motion-guided mechanical toy modeling. ACM Trans. Graph. 31, 6 (Nov.), 127:1–127:10. Google ScholarDigital Library
