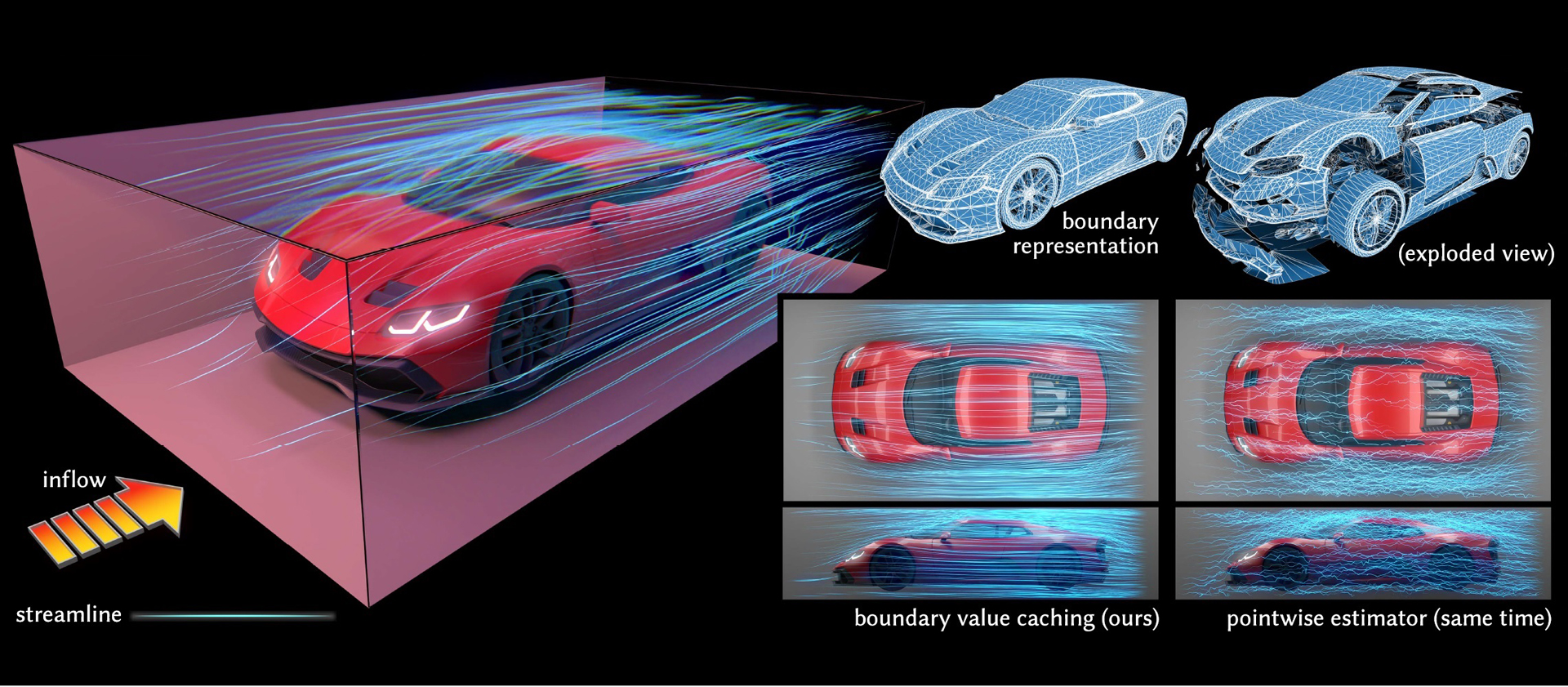
Boundary Value Caching for Walk on Spheres

Grid-free Monte Carlo methods such as walk on spheres can be used to solve elliptic partial differential equations without mesh generation or global solves. However, such methods independently estimate the solution at every point, and hence do not take advantage of the high spatial regularity of solutions to elliptic problems. We propose a fast caching strategy which first estimates solution values and derivatives at randomly sampled points along the boundary of the domain (or a local region of interest). These cached values then provide cheap, output-sensitive evaluation of the solution (or its gradient) at interior points, via a boundary integral formulation. Unlike classic boundary integral methods, our caching scheme introduces zero statistical bias and does not require a dense global solve. Moreover we can handle imperfect geometry (e.g., with self-intersections) and detailed boundary/source terms without repairing or resampling the boundary representation. Overall, our scheme is similar in spirit to virtual point light methods from photorealistic rendering: it suppresses the typical salt-and-pepper noise characteristic of independent Monte Carlo estimates, while still retaining the many advantages of Monte Carlo solvers: progressive evaluation, trivial parallelization, geometric robustness, etc. We validate our approach using test problems from visual and geometric computing.

References:

1. Gavin Barill, Neil G Dickson, Ryan Schmidt, David I W Levin, and Alec Jacobson. 2018. Fast Winding Numbers for Soups and Clouds. ACM Trans. Graph. 37, 4, Article 43 (jul 2018), 12 pages.
2. Ilia Binder and Mark Braverman. 2012. The rate of convergence of the walk on spheres algorithm. Geometric and Functional Analysis 22, 3 (2012), 558–587.
3. Benedikt Bitterli, Chris Wyman, Matt Pharr, Peter Shirley, Aaron Lefohn, and Wojciech Jarosz. 2020. Spatiotemporal Reservoir Resampling for Real-Time Ray Tracing with Dynamic Direct Lighting. ACM Trans. Graph. 39, 4, Article 148 (aug 2020), 17 pages.
4. Tony F Chan and Tarek P Mathew. 1994. Domain decomposition algorithms. Acta numerica 3 (1994), 61–143.
5. Wen Chen. 2002. Symmetric boundary knot method. Engineering Analysis with Boundary Elements 26, 6 (2002), 489–494.
6. Wen Chen. 2009. Singular boundary method: a novel, simple, meshfree, boundary collocation numerical method. Chinese Journal of Solid Mechanics 30, 6 (2009), 592–599.
7. Chris J Coleman, David L Tullock, and Nhan Phan-Thien. 1991. An effective boundary element method for inhomogeneous PDEs. J. App. Math. Phys. (ZAMP) 42, 5 (1991).
8. Martin Costabel. 1987. Principles of boundary element methods. Computer Physics Reports 6, 1–6 (1987), 243–274.
9. Carsten Dachsbacher, Jaroslav Křivánek, Miloš Hašan, Adam Arbree, Bruce Walter, and Jan Novák. 2014. Scalable realistic rendering with many-light methods. In Computer Graphics Forum, Vol. 33. Wiley Online Library, 88–104.
10. Graeme Fairweather and Andreas Karageorghis. 1998. The method of fundamental solutions for elliptic boundary value problems. Advances in Computational Mathematics 9, 1 (1998), 69–95.
11. Leslie Greengard and Vladimir Rokhlin. 1987. A fast algorithm for particle simulations. Journal of computational physics 73, 2 (1987), 325–348.
12. Jerry Jinfeng Guo and Elmar Eisemann. 2021. Geometric Sample Reweighting for Monte Carlo Integration. In Computer Graphics Forum, Vol. 40. Wiley Online Library, 109–119.
13. Toshiya Hachisuka and Henrik Wann Jensen. 2009. Stochastic Progressive Photon Mapping. ACM Trans. Graph. 28, 5 (dec 2009), 1–8.
14. Wolfgang Hackbusch. 2015. Hierarchical matrices: algorithms and analysis. Vol. 49. Springer.
15. Peter Hunter and Andrew Pullan. 2001. Fem/bem notes. Department of Engineering Science, The University of Auckland, New Zeland (2001).
16. Henrik Wann Jensen. 1996. Global illumination using photon maps. In Rendering Techniques’ 96: Proceedings of the Eurographics Workshop in Porto, Portugal, June 17–19, 1996 7. Springer, 21–30.
17. Alexander Keller. 1997. Instant Radiosity. In Proceedings of the 24th Annual Conference on Computer Graphics and Interactive Techniques (SIGGRAPH ’97). USA, 49–56.
18. Thomas Kollig and Alexander Keller. 2006. Illumination in the Presence of Weak Singularities. In Monte Carlo and Quasi-Monte Carlo Methods 2004. Springer Berlin Heidelberg, Berlin, Heidelberg, 245–257.
19. Daqi Lin and Cem Yuksel. 2020. Real-Time Stochastic Lightcuts. Proc. ACM Comput. Graph. Interact. Tech. 3, 1, Article 5 (may 2020), 18 pages.
20. Mervin E Muller. 1956. Some Continuous Monte Carlo Methods for the Dirichlet Problem. Annals of Mathematical Statistics 27, 3 (Sept. 1956), 569–589.
21. Yaobin Ouyang, Shiqiu Liu, Markus Kettunen, Matt Pharr, and Jacopo Pantaleoni. 2021. ReSTIR GI: Path Resampling for Real-Time Path Tracing. In Computer Graphics Forum, Vol. 40. Wiley Online Library, 17–29.
22. Paul William Partridge and Carlos Alberto Brebbia. 2012. Dual reciprocity boundary element method. Springer Science & Business Media.
23. Susanne Pfalzner and Paul Gibbon. 1997. Many-body tree methods in physics. Cambridge University Press.
24. Matt Pharr, Wenzel Jakob, and Greg Humphreys. 2016. Physically based rendering: From theory to implementation. Morgan Kaufmann.
25. Yang Qi, Dario Seyb, Benedikt Bitterli, and Wojciech Jarosz. 2022. A bidirectional formulation for Walk on Spheres. Computer Graphics Forum 41, 4 (2022), 51–62.
26. Damien Rioux-Lavoie, Ryusuke Sugimoto, Tümay Özdemir, Naoharu H Shimada, Christopher Batty, Derek Nowrouzezahrai, and Toshiya Hachisuka. 2022. A Monte Carlo Method for Fluid Simulation. ACM Trans. Graph. 41, 6, Article 240 (nov 2022), 16 pages.
27. Rohan Sawhney and Keenan Crane. 2020. Monte Carlo Geometry Processing: A Grid-Free Approach to PDE-Based Methods on Volumetric Domains. ACM Trans. Graph. 39, 4, Article 123 (aug 2020), 18 pages.
28. Rohan Sawhney, Bailey Miller, Ioannis Gkioulekas, and Keenan Crane. 2023. Walk on Stars: A Grid-Free Monte Carlo Method for PDEs with Neumann Boundary Conditions. ACM Trans. Graph. 42, 4 (aug 2023), 22 pages.
29. Rohan Sawhney, Dario Seyb, Wojciech Jarosz, and Keenan Crane. 2022. Grid-Free Monte Carlo for PDEs with Spatially Varying Coefficients. ACM Trans. Graph. 41, 4, Article 53 (jul 2022), 17 pages.
30. Benjamin Segovia, Jean-Claude Iehl, Richard Mitanchey, and Bernard Péroche. 2006. Bidirectional instant radiosity.. In Rendering Techniques. 389–397.
31. Alastair J Walker. 1974. New fast method for generating discrete random numbers with arbitrary frequency distributions. Electronics Letters 8, 10 (1974), 127–128.
32. Alastair J Walker. 1977. An Efficient Method for Generating Discrete Random Variables with General Distributions. ACM Trans. Math. Softw. 3, 3 (sep 1977), 253–256.
33. Bruce Walter, Sebastian Fernandez, Adam Arbree, Kavita Bala, Michael Donikian, and Donald P Greenberg. 2005. Lightcuts: A Scalable Approach to Illumination. ACM Trans. Graph. 24, 3 (jul 2005), 1098–1107.
34. Ekrem Fatih Yılmazer, Delio Vicini, and Wenzel Jakob. 2022. Solving Inverse PDE Problems using Grid-Free Monte Carlo Estimators. arXiv preprint arXiv:2208.02114 (2022).
35. Cem Yuksel. 2019. Stochastic Lightcuts. In Proceedings of the Conference on HighPerformance Graphics (Strasbourg, France) (HPG ’19). Eurographics Association, Goslar, DEU, 27–32.