“Bistable auxetic surface structures” by Chen, Panetta, Schnaubelt and Pauly

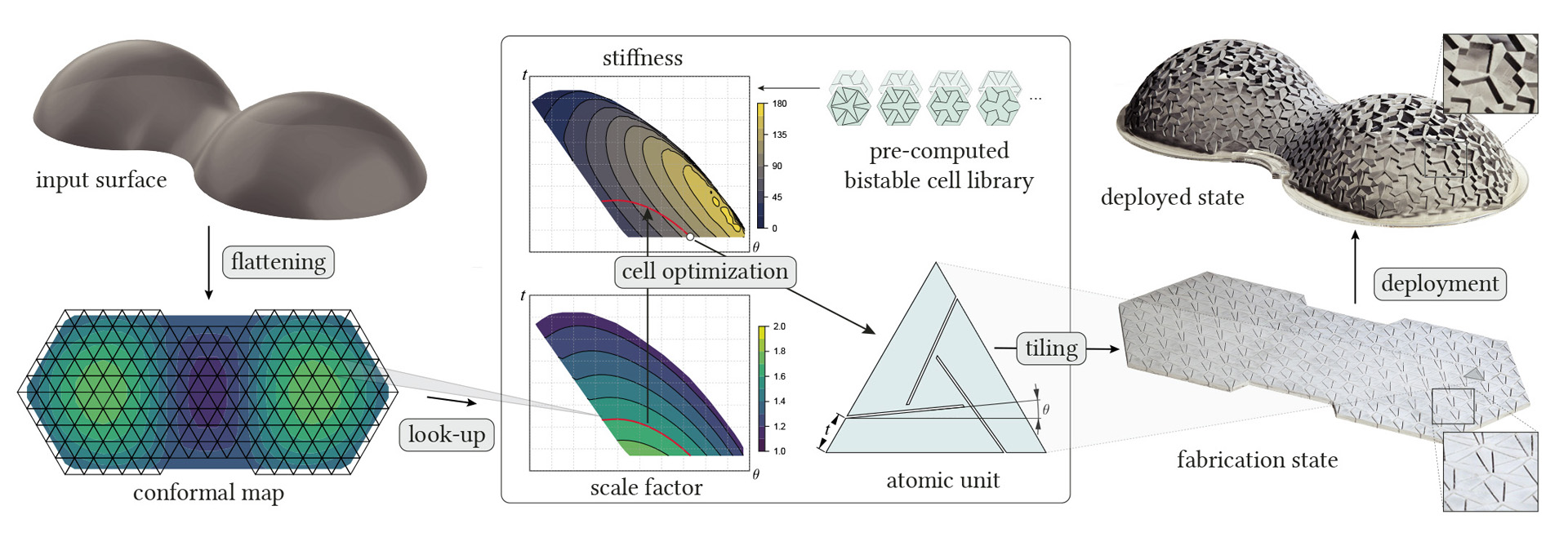
We present Bistable Auxetic Surface Structures, a novel deployable material system based on optimized bistable auxetic cells. Such a structure can be flat-fabricated from elastic sheet material, then deployed towards a desired double-curved target shape by activating the bistable mechanism of its component cells. A unique feature is that the deployed model is by design in a stable state. This facilitates deployment without the need of complex external supports or boundary constraints.We introduce a computational solution for the inverse design of our Bistable Auxetic Surface Structures. Our algorithm first precomputes a library of bistable auxetic cells to cover a range of in-plane expansion / contraction ratios, while maximizing the bistability and stiffness of the cell to ensure robust deployment. We then use metric distortion analysis of the target surface to compute the planar fabrication state as a composition of cells that best matches the desired deployment deformation. As each cell expands or contracts during deployment, metric frustration forces the surface towards its target equilibrium state. We validate our method with several physical prototypes.

1. Esther Rivas Adrover. 2015. Deployable structures. Laurence King Publishing, London.Google Scholar
2. Agisoft. 2021. Metashape, Ver. 1.7.1. https://www.agisoft.com/. Accessed: 2021-01-24.Google Scholar
3. Hillel Aharoni, Eran Sharon, and Raz Kupferman. 2014. Geometry of thin nematic elastomer sheets. Physical review letters 113, 25 (2014), 257801.Google Scholar
4. Hillel Aharoni, Yu Xia, Xinyue Zhang, Randall D Kamien, and Shu Yang. 2018. Universal inverse design of surfaces with thin nematic elastomer sheets. Proc. Natl. Acad. Sci. 115, 28 (2018), 7206–7211.Google ScholarCross Ref
5. Amit H. Bermano, Thomas Funkhouser, and Szymon Rusinkiewicz. 2017. State of the Art in Methods and Representations for Fabrication-Aware Design. Comput. Graph. Forum 36, 2 (May 2017), 509–535.Google ScholarCross Ref
6. Gaurav Bharaj, Danny Kaufman, Etienne Vouga, and Hanspeter Pfister. 2018. Meta-morphs: Bistable Planar Structures. arXiv:1804.06996 [cs.GR]Google Scholar
7. J William Boley, Wim M van Rees, Charles Lissandrello, Mark N Horenstein, Ryan L Truby, Arda Kotikian, Jennifer A Lewis, and L Mahadevan. 2019. Shape-shifting structured lattices via multimaterial 4D printing. Proc. Natl. Acad. Sci. 116, 42 (2019), 20856–20862.Google ScholarCross Ref
8. Paolo Celli, Connor McMahan, Brian Ramirez, Anton Bauhofer, Christina Naify, Douglas Hofmann, Basile Audoly, and Chiara Daraio. 2018. Shape-morphing architected sheets with non-periodic cut patterns. Soft matter 14, 48 (2018), 9744–9749.Google Scholar
9. Tian Chen, Osama R Bilal, Robert Lang, Chiara Daraio, and Kristina Shea. 2019. Autonomous deployment of a solar panel using elastic origami and distributed shape-memory-polymer actuators. Physical Review Applied 11, 6 (2019), 064069.Google ScholarCross Ref
10. Tian Chen, Jochen Mueller, and Kristina Shea. 2017. Integrated design and simulation of tunable, multi-state structures fabricated monolithically with multi-material 3D printing. Scientific reports 7, 1 (2017), 1–8.Google Scholar
11. Erik D. Demaine and Joseph O’Rourke. 2008. Geometric Folding Algorithms: Linkages, Origami, Polyhedra (reprint ed.). Cambridge University Press, USA.Google Scholar
12. Giulia E Fenci and Neil GR Currie. 2017. Deployable structures classification: A review. International Journal of Space Structures 32, 2 (2017), 112–130.Google ScholarCross Ref
13. Jan Friedrich, Sven Pfeiffer, and Christoph Gengnagel. 2018. Locally Varied Auxetic Structures for Doubly-Curved Shapes. Springer Singapore, Singapore, 323–336.Google Scholar
14. Akash Garg, Andrew O Sageman-Furnas, Bailin Deng, Yonghao Yue, Eitan Grinspun, Mark Pauly, and Max Wardetzky. 2014. Wire mesh design. ACM Trans. Graph. 33, 4 (2014), 1–12.Google ScholarDigital Library
15. Qi Ge, H Jerry Qi, and Martin L Dunn. 2013. Active materials by four-dimension printing. Applied Physics Letters 103, 13 (2013), 131901.Google Scholar
16. A Sydney Gladman, Elisabetta A Matsumoto, Ralph G Nuzzo, Lakshminarayanan Mahadevan, and Jennifer A Lewis. 2016. Biomimetic 4D printing. Nature materials 15, 4 (2016), 413–418.Google Scholar
17. Ruslan Guseinov, Connor McMahan, Jesús Pérez, Chiara Daraio, and Bernd Bickel. 2020. Programming temporal morphing of self-actuated shells. Nature communications 11, 1 (2020), 1–7.Google Scholar
18. Ruslan Guseinov, Eder Miguel, and Bernd Bickel. 2017. CurveUps: Shaping objects from flat plates with tension-actuated curvature. ACM Trans. Graph. 36, 4 (2017), 1–12.Google ScholarDigital Library
19. Lishuai Jin, Romik Khajehtourian, Jochen Mueller, Ahmad Rafsanjani, Vincent Tournat, Katia Bertoldi, and Dennis M. Kochmann. 2020. Guided transition waves in multistable mechanical metamaterials. Proc. Natl. Acad. Sci. 117, 5 (2020), 2319–2325.Google ScholarCross Ref
20. Mina Konaković, Keenan Crane, Bailin Deng, Sofien Bouaziz, Daniel Piker, and Mark Pauly. 2016. Beyond developable: computational design and fabrication with auxetic materials. ACM Trans. Graph. 35, 4 (2016), 1–11.Google ScholarDigital Library
21. Mina Konaković-Luković, Julian Panetta, Keenan Crane, and Mark Pauly. 2018. Rapid deployment of curved surfaces via programmable auxetics. ACM Trans. Graph. 37, 4 (2018), 1–13.Google ScholarDigital Library
22. Arda Kotikian, Ryan L Truby, John William Boley, Timothy J White, and Jennifer A Lewis. 2018. 3D printing of liquid crystal elastomeric actuators with spatially programed nematic order. Advanced materials 30, 10 (2018), 1706164.Google Scholar
23. Luigi Malomo, Jesús Pérez, Emmanuel Iarussi, Nico Pietroni, Eder Miguel, Paolo Cignoni, and Bernd Bickel. 2018. FlexMaps: Computational Design of Flat Flexible Shells for Shaping 3D Objects. ACM Trans. Graph. 37, 6, Article 241 (Dec. 2018), 14 pages.Google ScholarDigital Library
24. Koryo Miura. 1985. Method of packaging and deployment of large membranes in space. The Institute of Space and Astronautical Science report 618 (1985), 1–9.Google Scholar
25. P.B. Nakshatrala, D.A. Tortorelli, and K.B. Nakshatrala. 2013. Nonlinear structural design using multiscale topology optimization. Part I: Static formulation. Computer Methods in Applied Mechanics and Engineering 261-262 (2013), 167 — 176.Google Scholar
26. J. Panetta, M. Konaković-Luković, F. Isvoranu, E. Bouleau, and M. Pauly. 2019. X-Shells: A new class of deployable beam structures. ACM Trans. Graph. 38, 4 (2019), 1–15.Google ScholarDigital Library
27. Jesús Pérez, Miguel A. Otaduy, and Bernhard Thomaszewski. 2017. Computational Design and Automated Fabrication of Kirchhoff-plateau Surfaces. ACM Trans. Graph. 36, 4, Article 62 (July 2017), 12 pages.Google ScholarDigital Library
28. Nico Pietroni, Bernd Bickel, Luigi Malomo, and Paolo Cignoni. 2019. State of the Art on Stylized Fabrication. In SIGGRAPH Asia 2019 Courses (Brisbane, Queensland, Australia) (SA ’19). Association for Computing Machinery, New York, NY, USA, Article 118, 1 pages.Google Scholar
29. Stefan Pillwein, Kurt Leimer, Michael Birsak, and Przemyslaw Musialski. 2020. On Elastic Geodesic Grids and Their Planar to Spatial Deployment. ACM Trans. Graph. 39, 4, Article 125 (July 2020), 12 pages.Google ScholarDigital Library
30. Ahmad Rafsanjani and Damiano Pasini. 2016. Bistable auxetic mechanical metamaterials inspired by ancient geometric motifs. Extreme Mechanics Letters 9 (2016), 291–296.Google ScholarCross Ref
31. Dan Raviv et al. 2014. Active printed materials for complex self-evolving deformations. Scientific reports 4 (2014), 7422.Google Scholar
32. Rohan Sawhney and Keenan Crane. 2017. Boundary first flattening. ACM Trans. Graph. 37, 1 (2017), 1–14.Google ScholarDigital Library
33. Yan Shi, Fan Zhang, Kewang Nan, Xueju Wang, Juntong Wang, Yijie Zhang, Yutong Zhang, Haiwen Luan, Keh-Chih Hwang, Yonggang Huang, John A. Rogers, and Yihui Zhang. 2017. Plasticity-induced origami for assembly of three dimensional metallic structures guided by compressive buckling. Extreme Mechanics Letters 11 (2017), 105 — 110.Google ScholarCross Ref
34. J. Shim, C. Perdigou, E. R. Chen, Katia Bertoldi, and P. M. Reis. 2012. Buckling-induced encapsulation of structured elastic shells under pressure. Proc. Natl. Acad. Sci. 109, 16 (2012), 5978–5983.Google ScholarCross Ref
35. Emmanuel Siéfert, Etienne Reyssat, José Bico, and Benoit Roman. 2019. Bio-inspired pneumatic shape-morphing elastomers. Nature materials 18, 1 (2019), 24–28.Google Scholar
36. T. Tachi. 2009. Origamizing Polyhedral Surfaces. IEEE Transactions on Visualization and Computer Graphics 16, 2 (2009), 298–311.Google ScholarDigital Library