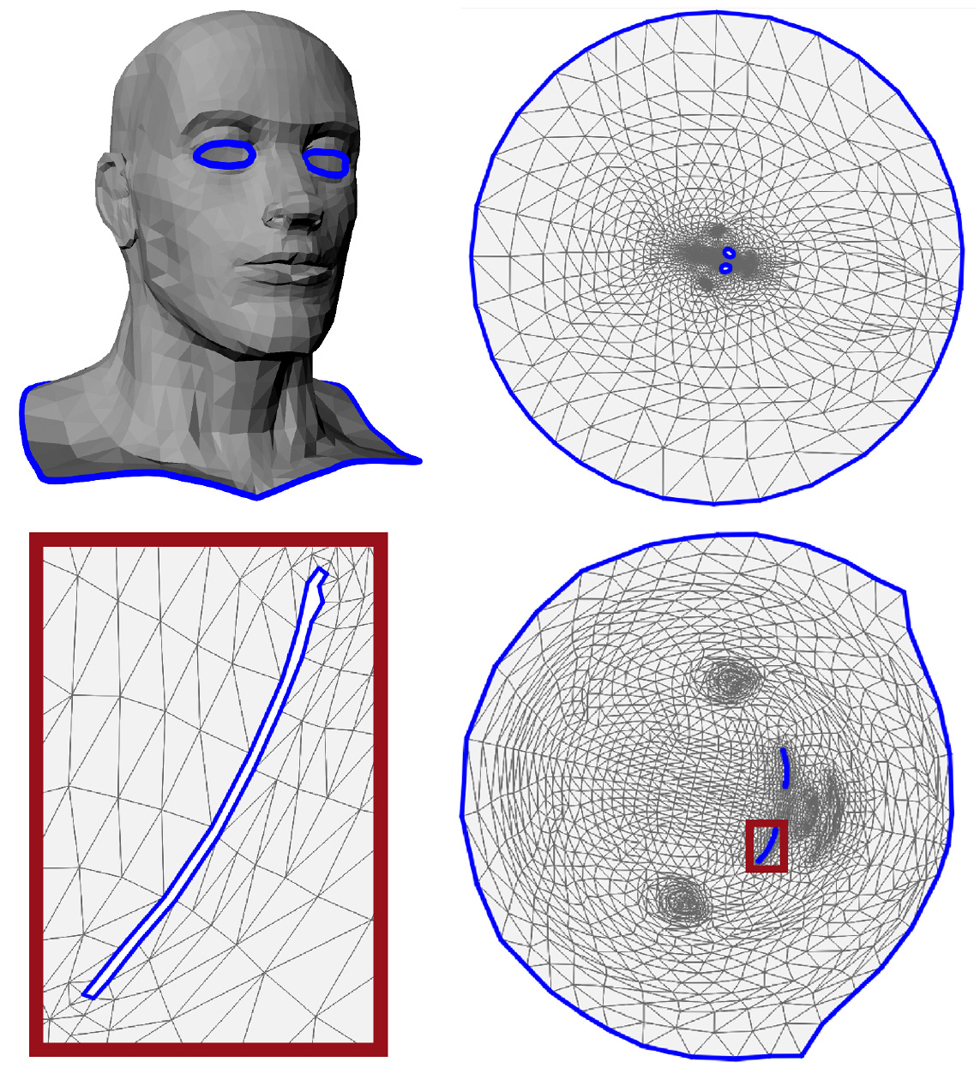
“Bijective parameterization with free boundaries”
Conference:
Type(s):
Title:
- Bijective parameterization with free boundaries
Session/Category Title: Parameterization & Mapping
Presenter(s)/Author(s):
Moderator(s):
Abstract:
We present a fully automatic method for generating guaranteed bijective surface parameterizations from triangulated 3D surfaces partitioned into charts. We do so by using a distortion metric that prevents local folds of triangles in the parameterization and a barrier function that prevents intersection of the chart boundaries. In addition, we show how to modify the line search of an interior point method to directly compute the singularities of the distortion metric and barrier functions to maintain a bijective map. By using an isometric metric that is efficient to compute and a spatial hash to accelerate the evaluation and gradient of the barrier function for the boundary, we achieve fast optimization times. Unlike previous methods, we do not require the boundary be constrained by the user to a non-intersecting shape to guarantee a bijection, and the boundary of the parameterization is free to change shape during the optimization to minimize distortion.
References:
1. Aigerman, N., Poranne, R., and Lipman, Y. 2014. Lifted bijections for low distortion surface mappings. ACM Trans. Graph. 33, 4, 69:1–69:12. Google ScholarDigital Library
2. Bommes, D., Zimmer, H., and Kobbelt, L. 2009. Mixed-integer quadrangulation. ACM Trans. Graph. 28, 3, 77:1–77:10. Google ScholarDigital Library
3. Burley, B., and Lacewell, D. 2008. Ptex: Per-face texture mapping for production rendering. In Eurographics Symposium on Rendering, 1155–1164. Google ScholarDigital Library
4. Degener, P., Meseth, J., and Klein, R. 2003. An adaptable surface parameterization method. In Proceedings of the 12th International Meshing Roundtable, 201–213.Google Scholar
5. Floater, M. S., and Hormann, K. 2005. Surface parameterization: a tutorial and survey. In In Advances in Multiresolution for Geometric Modelling, Mathematics and Visualization, 157–186.Google Scholar
6. Floater, M. S. 1997. Parametrization and smooth approximation of surface triangulations. Computer Aided Geometric Design 14, 231–250. Google ScholarDigital Library
7. Forsgren, A., Gill, P. E., and Wright, M. H. 2002. Interior methods for nonlinear optimization. SIAM Review 44, 4, 525–597. Google ScholarDigital Library
8. Hormann, K., and Greiner, G. 2000. MIPS: An efficient global parametrization method. In Curve and Surface Design: Saint-Malo 1999. 153–162.Google Scholar
9. Hormann, K., Lévy, B., and Sheffer, A. 2007. Mesh parameterization: Theory and practice. In ACM SIGGRAPH Courses. Google ScholarDigital Library
10. Lévy, B., Petitjean, S., Ray, N., and Maillot, J. 2002. Least squares conformal maps for automatic texture atlas generation. ACM Trans. Graph. 21, 3, 362–371. Google ScholarDigital Library
11. Lipman, Y. 2012. Bounded distortion mapping spaces for triangular meshes. ACM Trans. Graph. 31, 4, 108:1–108:13. Google ScholarDigital Library
12. Liu, L., Zhang, L., Xu, Y., Gotsman, C., and Gortler, S. J. 2008. A local/global approach to mesh parameterization. In Symposium on Geometry Processing, 1495–1504. Google ScholarDigital Library
13. Mullen, P., Tong, Y., Alliez, P., and Desbrun, M. 2008. Spectral conformal parameterization. In Symposium on Geometry Processing, 1487–1494. Google ScholarDigital Library
14. Nocedal, J. 1980. Updating quasi-newton matrices with limited storage. Mathematics of Computation 35, 151, pp. 773–782.Google ScholarCross Ref
15. Pinkall, U., and Polthier, K. 1993. Computing discrete minimal surfaces and their conjugates. Experimental Mathematics 2, 15–36.Google ScholarCross Ref
16. Poranne, R., and Lipman, Y. 2014. Provably good planar mappings. ACM Trans. Graph. 33, 4, 76:1–76:11. Google ScholarDigital Library
17. Purnomo, B., Cohen, J. D., and Kumar, S. 2004. Seamless texture atlases. In Symposium on Geometry Processing, 65–74. Google ScholarDigital Library
18. Sanan, P. D. 2014. Geometric elasticity for graphics, simulation, and computation. PhD thesis, Caltech. Google ScholarDigital Library
19. Sander, P. V., Snyder, J., Gortler, S. J., and Hoppe, H. 2001. Texture mapping progressive meshes. In ACM SIGGRAPH, 409–416. Google ScholarDigital Library
20. Schneider, T., Hormann, K., and Floater, M. S. 2013. Bijective composite mean value mappings. In Symposium on Geometry Processing, 137–146. Google ScholarDigital Library
21. Schreiner, J., Asirvatham, A., Praun, E., and Hoppe, H. 2004. Inter-surface mapping. In ACM SIGGRAPH, 870–877. Google ScholarDigital Library
22. Schüller, C., Kavan, L., Panozzo, D., and Sorkinehornung, O. 2013. Locally injective mappings. In Symposium on Geometry Processing, 125–135. Google ScholarDigital Library
23. Sheffer, A., and de Sturler, E. 2001. Parameterization of faceted surfaces for meshing using angle-based flattening. Engineering with Computers 17, 3, 326–337.Google ScholarCross Ref
24. Sheffer, A., Lévy, B., Mogilnitsky, M., and Bogomyakov, A. 2005. Abf++: Fast and robust angle based flattening. ACM Trans. Graph. 24, 2, 311–330. Google ScholarDigital Library
25. Sheffer, A., Praun, E., and Rose, K. 2006. Mesh parameterization methods and their applications. Found. Trends. Comput. Graph. Vis. 2, 2, 105–171. Google ScholarDigital Library
26. Sorkine, O., Cohen-Or, D., Goldenthal, R., and Lischinski, D. 2002. Bounded-distortion piecewise mesh parameterization. In Proceedings of the Conference on Visualization, 355–362. Google ScholarDigital Library
27. Springborn, B., Schröder, P., and Pinkall, U. 2008. Conformal equivalence of triangle meshes. ACM Trans. Graph. 27, 3, 77:1–77:11. Google ScholarDigital Library
28. Tutte, W. T. 1963. How to draw a graph. Proceedings of the London Mathematical Society 13, 3, 743–768.Google ScholarCross Ref
29. Weber, O., and Zorin, D. 2014. Locally injective parametrization with arbitrary fixed boundaries. ACM Trans. Graph. 33, 4, 75:1–75:12. Google ScholarDigital Library
30. Wolfe, P. 1969. Convergence conditions for ascent methods. SIAM Review 11, 2, 226–235.Google ScholarDigital Library
31. Yuksel, C., Keyser, J., and House, D. H. 2010. Mesh colors. ACM Transactions on Graphics 29, 2, 15:1–15:11. Google ScholarDigital Library
32. Zhang, E., Mischaikow, K., and Turk, G. 2005. Featurebased surface parameterization and texture mapping. ACM Trans. Graph. 24, 1 (Jan.), 1–27. Google ScholarDigital Library
33. Zhou, K., Synder, J., Guo, B., and Shum, H.-Y. 2004. Iso-charts: Stretch-driven mesh parameterization using spectral analysis. In Symposium on Geometry Processing, 45–54. Google ScholarDigital Library