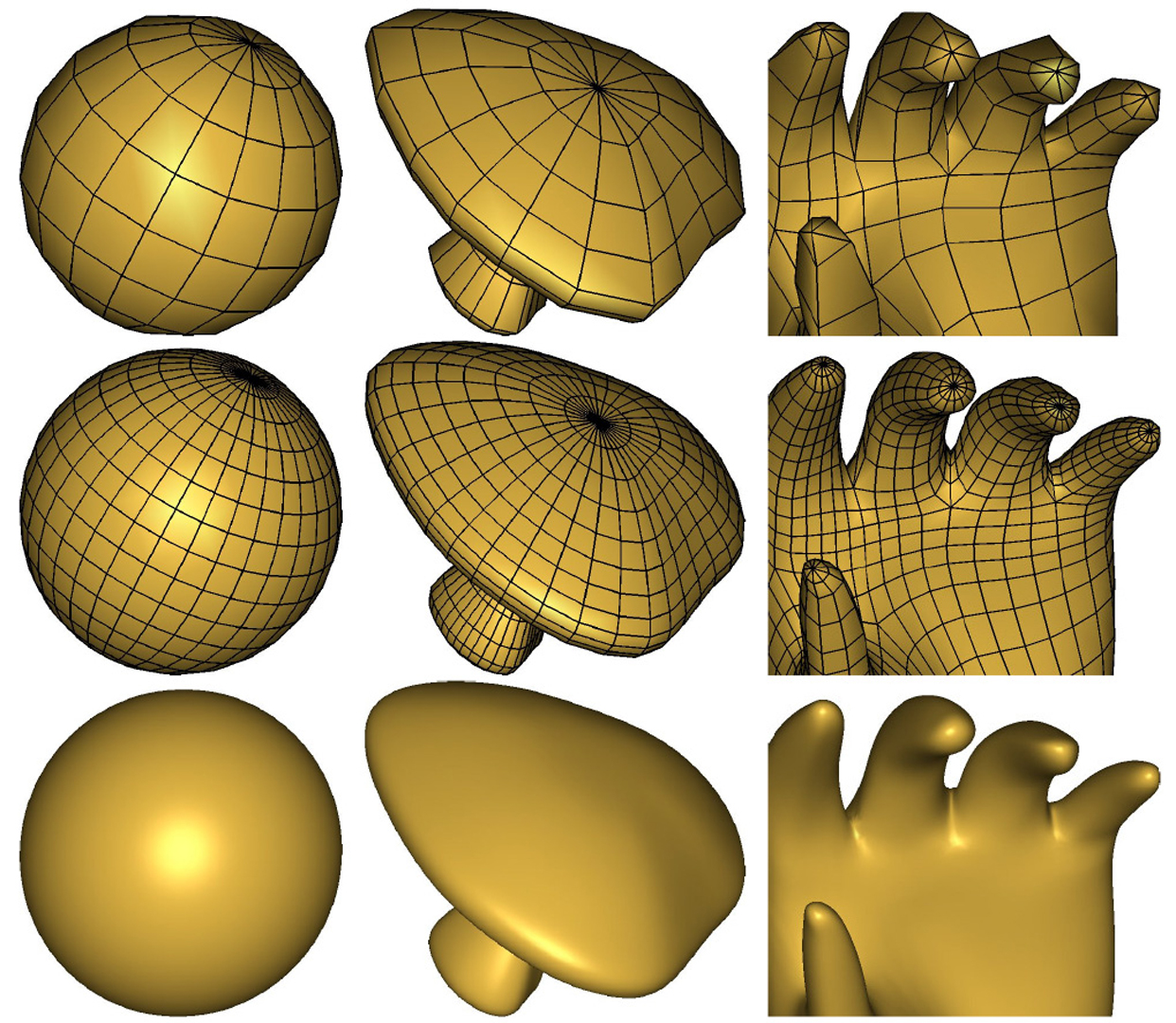
“Bi-3 C2 polar subdivision” by Myles and Peters

Popular subdivision algorithms like Catmull-Clark and Loop are C2 almost everywhere, but suffer from shape artifacts and reduced smoothness exactly near the so-called “extraordinary vertices” that motivate their use. Subdivision theory explains that inherently, for standard stationary subdivision algorithms, curvature-continuity and the ability to model all quadratic shapes requires a degree of at least bi-6. The existence of a simple-to-implement C2 subdivision algorithm generating surfaces of good shape and piecewise degree bi-3 in the polar setting is therefore a welcome surprise. This paper presents such an algorithm, the underlying insights, and a detailed analysis. In bi-3 C2 polar subdivision the weights depend, as in standard schemes, only on the valence, but the valence at one central polar vertex increases to match Catmull-Clark-refinement.

1. Catmull, E., and Clark, J. 1978. Recursively generated B-spline surfaces on arbitrary topological meshes. Computer Aided Design 10, 350–355.Google ScholarCross Ref
2. Choi, Y.-J., Lee, Y. J., Yoon, J., Lee, B.-G., and Kim, Y. J. 2006. A new class of non-stationary interpolatory subdivision schemes based on exponential polynomials. In Geometric Modeling and Processing, 563–570. Google ScholarDigital Library
3. Farin, G. 1997. Curves and Surfaces for Computer-Aided Geometric Design: A Practical Guide, fourth ed. Academic Press, San Diego, CA, USA. Google ScholarDigital Library
4. Karčiauskas, K., Myles, A., and Peters, J. 2006. A C
2 polar jet subdivision. In SGP ’06: Proceedings of the Fourth Eurographics Symposium on Geometry Processing, Eurographics Association, Aire-la-Ville, Switzerland, Switzerland, 173–180. Google ScholarDigital Library
5. Karčiauskas, K., and Peters, J. 2007. Concentric tessellation maps and curvature continuous guided surfaces. Comput. Aided Geom. Des. 24, 2, 99–111. Google ScholarDigital Library
6. Karčiauskas, K., and Peters, J. 2007. On the curvature of guided surfaces. Tech. rep., University of Florida CISE, REP-2007-430, Gainesville, FL, USA.Google Scholar
7. Karčiauskas, K., and Peters, J. 2007. Bicubic polar subdivision. ACM Trans. Graph. 26, 4, 14. Google ScholarDigital Library
8. Karčiauskas, K., and Peters, J. 2008. On the curvature of guided surfaces. Comput. Aided Geom. Des. 25, 2, 69–79. Google ScholarDigital Library
9. Levin, A. 2006. Modified subdivision surfaces with continuous curvature. In SIGGRAPH ’06: ACM SIGGRAPH 2006 Papers, ACM Press, New York, NY, USA, 1035–1040. Google ScholarDigital Library
10. Loop, C. T., and Schaefer, S. 2008. G
2 tensor product splines over extraordinary vertices. Computer Graphics Forum (Proceedings of 2008 Symposium on Geometry Processing) 27, 5, 1373–1382. Google ScholarDigital Library
11. Loop, C. T. 2004. Second order smoothness over extraordinary vertices. In SGP ’04: Proceedings of the 2004 Eurographics/ACM SIGGRAPH Symposium on Geometry Processing, ACM, New York, NY, USA, 165–174. Google ScholarDigital Library
12. Lutterkort, D., and Peters, J. 2001. Tight linear envelopes for splines. Numerische Mathematik 89, 4 (Oct), 735–748.Google ScholarCross Ref
13. Morin, G., Warren, J. D., and Weimer, H. 2001. A subdivision scheme for surfaces of revolution. Comput. Aided Geom. Des. 18, 5, 483–502. Google ScholarDigital Library
14. Myles, A., Karčiauskas, K., and Peters, J. 2008. Pairs of bi-cubic surface constructions supporting polar connectivity. Comput. Aided Geom. Des. 25, 8, 621–630. Google ScholarDigital Library
15. Myles, A. 2008. Curvature-continuous bicubic subdivision surfaces for polar configurations. PhD thesis, University of Florida, Gainesville, Florida. Google ScholarDigital Library
16. Peters, J., and Reif, U. 2008. Subdivision Surfaces. Geometry and Computing, Vol. 3. Springer-Verlag New York, Inc., New York, NY, USA, Apr. Google ScholarDigital Library
17. Peters, J. 2002. C
2 free-form surfaces of degree (3,5). Comput. Aided Geom. Des. 19, 2, 113–126. Google ScholarDigital Library
18. Prautzsch, H., and Reif, U. 1999. Degree estimates for C
k-piecewise polynomial subdivision surfaces. Advances in Computational Mathematics 10, 2, 209–217.Google ScholarCross Ref
19. Prautzsch, H., and Reif, U. 1999. Necessary conditions for subdivision surfaces. Advances in Computational Mathematics 10, 209–217.Google ScholarCross Ref
20. Prautzsch, H., and Umlauf, G. 1998. A G
2-subdivision algorithm. In Geometric Modeling, Dagstuhl, Germany, 1996, Springer-Verlag, London, UK, 217–224. Google ScholarDigital Library
21. Prautzsch, H., Boehm, W., and Paluszny, M. 2002. Bezier and B-Spline Techniques. Springer-Verlag New York, Inc., Secaucus, NJ, USA. Google ScholarDigital Library
22. Prautzsch, H. 1997. Freeform splines. Comput. Aided Geom. Des. 14, 3, 201–206. Google ScholarDigital Library
23. Reif, U. 1998. TURBS—topologically unrestricted rational B-splines. Constructive Approximation. An International Journal for Approximations and Expansions 14, 1, 57–77.Google Scholar
24. Wallner, J., and Dyn, N. 2005. Convergence and C
1 analysis of subdivision schemes on manifolds by proximity. Comput. Aided Geom. Des. 22, 7, 593–622. Google ScholarDigital Library
25. Ying, L., and Zorin, D. 2004. A simple manifold-based construction of surfaces of arbitrary smoothness. ACM Trans. Graph. 23, 3 (Aug.), 271–275. Google ScholarDigital Library
26. Zhang, H., and Wang, G. 2002. Semi-stationary subdivision operators in geometric modeling. Progress in National Science 12, 10, 772–776.Google Scholar
27. Zorin, D. 2006. Constructing curvature-continuous surfaces by blending. In SGP ’06: Proceedings of the Fourth Eurographics Symposium on Geometry Processing, Eurographics Association, Aire-la-Ville, Switzerland, Switzerland, 31–40. Google ScholarDigital Library
28. Zulti, A., Levin, A., Levin, D., and Teicher, M. 2006. C
2 subdivision over triangulations with one extraordinary point. Comput. Aided Geom. Des. 23, 2, 157–178. Google ScholarDigital Library