“Automatic extraction of Irregular Network digital terrain models” by Fowler and Little
Conference:
Type(s):
Title:
- Automatic extraction of Irregular Network digital terrain models
Presenter(s)/Author(s):
Abstract:
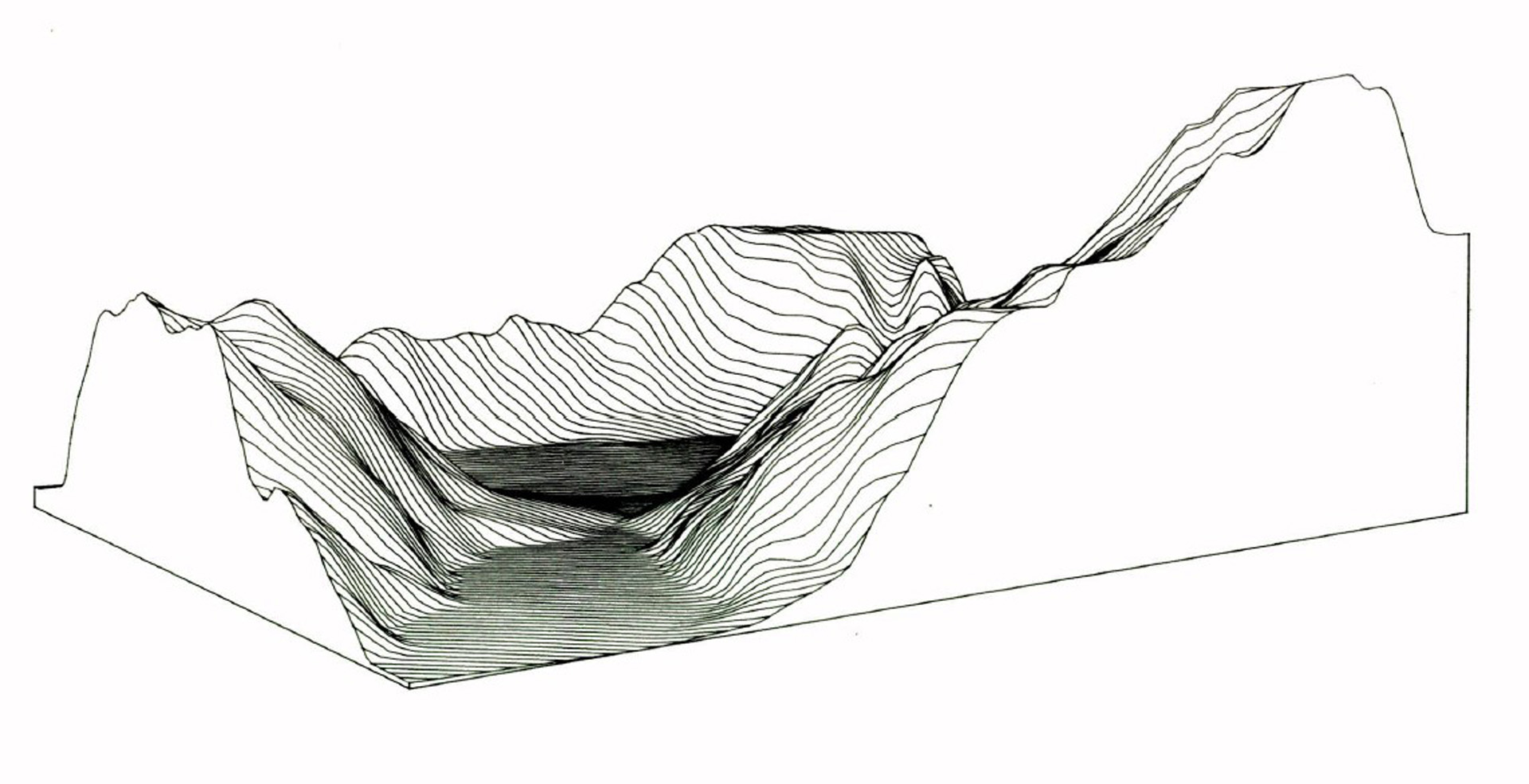
For representation of terrain, an efficient alternative to dense grids is the Triangulated Irregular Network (TIN), which represents a surface as a set of non-overlapping contiguous triangular facets, of irregular size and shape. The source of digital terrain data is increasingly dense raster models produced by automated orthophoto machines or by direct sensors such as synthetic aperture radar. A method is described for automatically extracting a TIN model from dense raster data. An initial approximation is constructed by automatically triangulating a set of feature points derived from the raster model. The method works by local incremental refinement of this model by the addition of new points until a uniform approximation of specified tolerance is obtained. Empirical results show that substantial savings in storage can be obtained.
References:
1. Bauhuber, F., Erlacher, V. and Gunther, P. A programming system for the manipulation of digital terrain models (in German). Organ der Deutschen Gesellschaft fur Photogrammetrie 43, (1975), 104-107.
2. Delaunay, B. “Sur la sphere vide”, Bulletin of the Academy of Sciences of USSR, VII, Classe. Sci. Mat. Nat. (1934), 793-800.
3. Douglas, D.H. and Peucker T.K. Algorithms for the reduction of the number of points required to represent a digitized line or its caricature. Canadian Cartographer 10, 2 (December 1973), 112-122.
4. Duda, R.O. and Hart, P.E. Pattern Classification and Scene Analysis, New York, (1973).
5. Fowler, R.J. Approaches to multi-dimensional searching, in Dutton, Geoffrey (Ed.), Harvard Papers on Geographic Information Systems 6, Addison-Wesley, Reading, Ma., 1978.
6. Fowler, R.J. DELTRI: An efficient program for producing Delaunay triangulations. Technical Report 18, ONR Contract N00014-75-c-0886, Dept. of Geography, Simon Fraser University, Burnaby, B.C., Canada, 1977.
7. Gates, W.E. and Associates, Inc. A land-based modelling system for water quality management studies, Report for Virginia Electric and Power, 1974.
8. Gold, C.M., Charters, T.D. and Ramsden, J. Automated contour mapping using triangular element data structures and an interpolant over each irregular triangular domain. Proceedings of SIGGRAPH ’77, San Jose, California (1977), 170-175.
9. Mark, D.M. Computer analysis of topography: a comparison of terrain storage methods. Geografiska Annaler 57, (1975), 179-188.
10. Peucker, T.K. and Douglas, D.H. Detection of surface-specific points by local parallel processing of discrete terrain elevation data. Computer Graphics and Image Processing 4, (1975), 375-387.
11. Peucker, T.K., Fowler, R.J., Little, J.J. and Mark, D.M. Digital representation of three-dimensional surfaces by triangulated irregular networks (TIN). Technical Report 10, ONR Contract #N00014-75-C-0886, Dept. Geography, Simon Fraser University, Burnaby, B.C., Canada, 1977.
12. Peucker, T.K., Fowler, R.J. and Little, J.J. The triangulated irregular network. Proceedings of the ASP-ACSM Symposium on DTM’s. St. Louis, Missouri, October 1978.
13. Pike, R.J. and Rozema, W.J. Spectral analysis of landforms. Annals of the Association of American Geographers 65, 4 (1975), 449-516.
14. Proceedings of ASP-ACSM Symposium on DTM’s. St. Louis, Missouri, May 1978.
15. Ramer, U. An iterative procedure for the polygonal approximation of planar curves. Computer Graphics and Image Processing 1, 3 (Nov. 1972).
16. Rogers, C. Packing and Covering. Cambridge University Press, Cambridge, 1964.
17. Shamos, M.I. and Hoey, D. Geometric intersection problems. Proc. 17th Annual IEEE Symposium on the Foundations of Computer Science, (October 1976), 208-215.
18. Warntz, W. The topology of a socio-economic terrain and spatial flows. Regional Science Association Papers 17, (1966) 47-61.