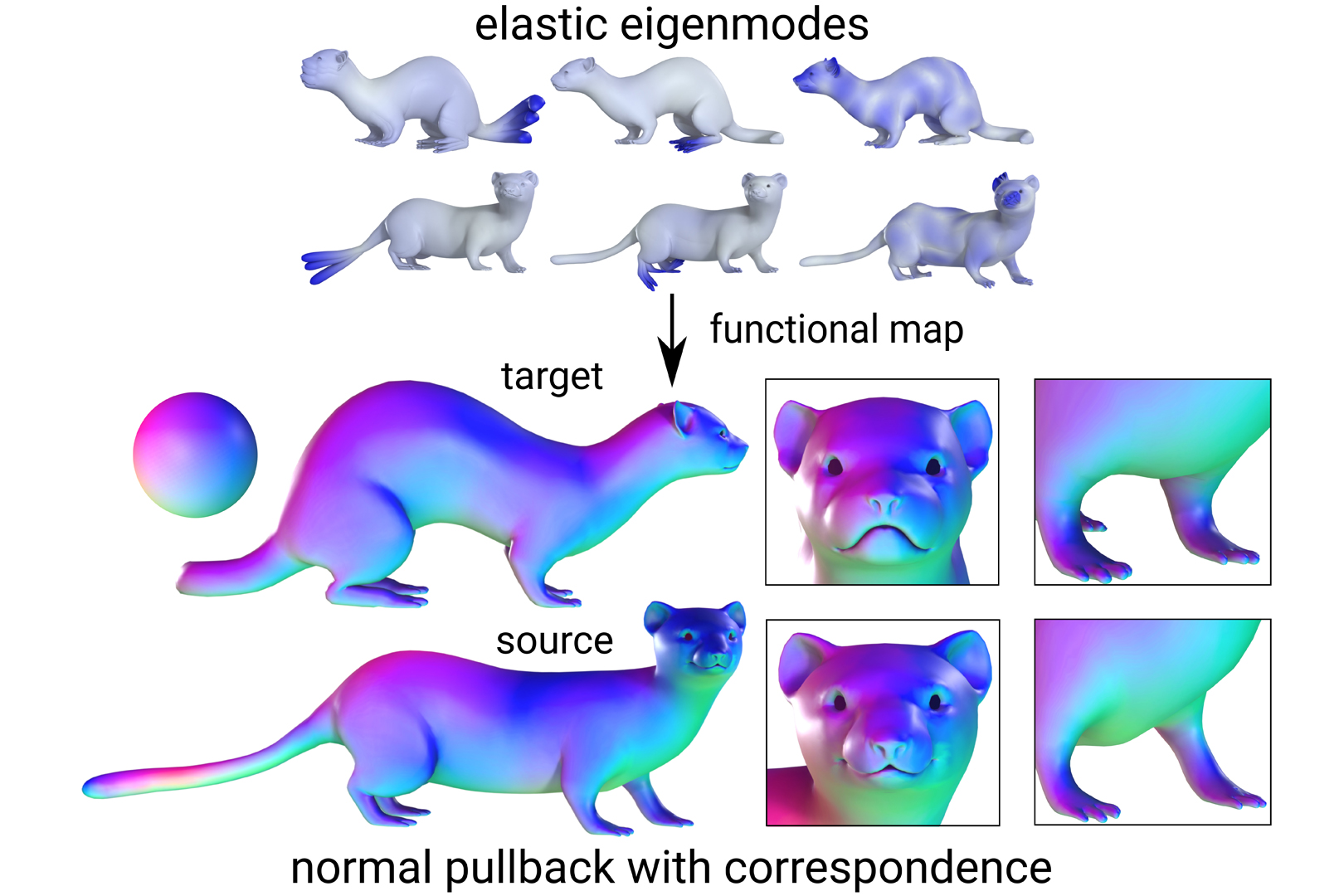
“An Elastic Basis for Spectral Shape Correspondence” by Hartwig, Sassen, Azencot, Rumpf and Ben-Chen
Conference:
Type(s):
Title:
- An Elastic Basis for Spectral Shape Correspondence
Session/Category Title: Marvelous Mappings
Presenter(s)/Author(s):
Moderator(s):
Abstract:
Finding correspondences between shapes is a central task in geometry processing with applications such as texture or deformation transfer and shape interpolation. We develop a spectral method for finding correspondences between non-isometric shapes that aligns extrinsic features. For this, we propose a novel crease aware spectral basis, that is derived from the Hessian of an elastic thin shell energy. We incorporate this basis in a functional map framework and demonstrate the effectiveness of our approach for mapping non-isometric shapes such that prominent features are put in correspondence. Finally, we describe the necessary adaptations to the functional map framework for working with non-orthogonal basis functions, thus considerably widening the scope of future uses of spectral shape correspondence.
References:
1. Dragomir Anguelov, Praveen Srinivasan, Daphne Koller, Sebastian Thrun, Jim Rodgers, and James Davis. 2005. Shape Completion and Animation of People. ACM Transactions on Graphics (TOG) 24, 3 (2005), 408.
2. Omri Azencot and Rongjie Lai. 2021. A Data-Driven Approach to Functional Map Construction and Bases Pursuit. Computer Graphics Forum 40, 5 (aug 2021), 97–110. https://doi.org/10.1111/cgf.14360
3. Federica Bogo, Javier Romero, Matthew Loper, and Michael J Black. 2014. FAUST: Dataset and evaluation for 3D mesh registration. In Proceedings of the IEEE conference on computer vision and pattern recognition. IEEE, 3794–3801.
4. Etienne Corman, Justin Solomon, Mirela Ben-Chen, Leonidas Guibas, and Maks Ovsjanikov. 2017. Functional characterization of intrinsic and extrinsic geometry. ACM Transactions on Graphics (TOG) 36, 2 (2017), 1–17.
5. Roberto M. Dyke, Yu-Kun Lai, Paul L. Rosin, Stefano Zappalà, Seana Dykes, Daoliang Guo, Kun Li, Riccardo Marin, Simone Melzi, and Jingyu Yang. 2020. SHREC’20: Shape correspondence with non-isometric deformations. Computers & Graphics 92 (2020), 28–43. https://doi.org/10.1016/j.cag.2020.08.008
6. Michal Edelstein, Danielle Ezuz, and Mirela Ben-Chen. 2020. ENIGMA. ACM Transactions on Graphics (TOG) 39, 4 (jul 2020), 16 pages. https://doi.org/10.1145/3386569.3392447
7. Marvin Eisenberger, Zorah Lahner, and Daniel Cremers. 2020. Smooth shells: Multi-scale shape registration with functional maps. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. IEEE Computer Society, 12265–12274.
8. Danielle Ezuz and Mirela Ben-Chen. 2017. Deblurring and denoising of maps between shapes. In Computer Graphics Forum, Vol. 36. The Eurographs Association & John Wiley & Sons, Ltd. Chichester, UK, 165–174.
9. D. Ezuz, B. Heeren, O. Azencot, M. Rumpf, and M. Ben-Chen. 2019a. Elastic Correspondence between Triangle Meshes. Computer Graphics Forum 38, 2 (may 2019), 121–134. https://doi.org/10.1111/cgf.13624
10. Danielle Ezuz, Justin Solomon, and Mirela Ben-Chen. 2019b. Reversible harmonic maps between discrete surfaces. ACM Transactions on Graphics (TOG) 38, 2 (2019), 1–12.
11. Daniela Giorgi, Silvia Biasotti, and Laura Paraboschi. 2007. Shape retrieval contest 2007: Watertight models track. SHREC competition 8, 7 (2007), 7.
12. Eitan Grinspun, Anil N Hirani, Mathieu Desbrun, and Peter Schröder. 2003. Discrete shells. In Proceedings of the 2003 ACM SIGGRAPH/Eurographics symposium on Computer animation. Citeseer, 62–67.
13. Behrend Heeren, Martin Rumpf, Peter Schröder, Max Wardetzky, and Benedikt Wirth. 2014. Exploring the geometry of the space of shells. In Computer Graphics Forum, Vol. 33. 247–256.
14. Klaus Hildebrandt, Christian Schulz, Christoph von Tycowicz, and Konrad Polthier. 2011. Interactive surface modeling using modal analysis. ACM Transactions on Graphics (TOG) 30, 5 (2011), 1–11.
15. Klaus Hildebrandt, Christian Schulz, Christoph von Tycowicz, and Konrad Polthier. 2010. Eigenmodes of surface energies for shape analysis. In International Conference on Geometric Modeling and Processing. Springer, 296–314.
16. Klaus Hildebrandt, Christian Schulz, Christoph von Tycowicz, and Konrad Polthier. 2012. Modal shape analysis beyond Laplacian. Computer Aided Geometric Design 29, 5 (2012), 204–218.
17. Qi-Xing Huang, Martin Wicke, Bart Adams, and Leonidas Guibas. 2009. Shape decomposition using modal analysis. In Computer Graphics Forum, Vol. 28. Wiley Online Library, 407–416.
18. Vladimir G Kim, Yaron Lipman, and Thomas Funkhouser. 2011. Blended intrinsic maps. ACM transactions on graphics (TOG) 30, 4 (2011), 1–12.
19. Robin Magnet. 2022. pyFM: Python bindings for functional maps. https://github.com/RobinMagnet/pyFM.
20. Robin Magnet, Jing Ren, Olga Sorkine-Hornung, and Maks Ovsjanikov. 2022. Smooth Non-Rigid Shape Matching via Effective Dirichlet Energy Optimization. In International Conference on 3D Vision.
21. Riccardo Marin, Marie-Julie Rakotosaona, Simone Melzi, and Maks Ovsjanikov. 2020. Correspondence learning via linearly-invariant embedding. Advances in Neural Information Processing Systems 33 (2020), 1608–1620.
22. Simone Melzi, Riccardo Marin, Pietro Musoni, Filippo Bardon, Marco Tarini, and Umberto Castellani. 2020. Intrinsic/extrinsic embedding for functional remeshing of 3D shapes. Computers & Graphics 88 (2020), 1–12.
23. S Melzi, R Marin, P Musoni, U Castellani, M Tarini, 2019a. Visual assessments of functional maps. In Symposium on Geometry Processing 2019-Posters. The Eurographics Association, 5–6.
24. Simone Melzi, Jing Ren, Kaust Rodolà, Abhishek Sharma, Maks Ovsjanikov, and Peter Wonka. 2019b. ZoomOut: Spectral Upsampling for Efficient Shape Correspondence. ACM Transactions on Graphics (TOG) 38, 6 (2019), 1–14.
25. Maks Ovsjanikov, Mirela Ben-Chen, Justin Solomon, Adrian Butscher, and Leonidas Guibas. 2012. Functional maps: a flexible representation of maps between shapes. ACM Transactions on Graphics (TOG) 31, 4 (2012), 1–11.
26. Maks Ovsjanikov, Etienne Corman, Michael Bronstein, Emanuele Rodolà, Mirela Ben-Chen, Leonidas Guibas, Frederic Chazal, and Alex Bronstein. 2016. Computing and processing correspondences with functional maps. In SIGGRAPH ASIA 2016 Courses. 1–60.
27. Gautam Pai, Jing Ren, Simone Melzi, Peter Wonka, and Maks Ovsjanikov. 2021. Fast Sinkhorn filters: Using matrix scaling for non-rigid shape correspondence with functional maps. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 384–393.
28. Mikhail Panine, Maxime Kirgo, and Maks Ovsjanikov. 2022. Non-Isometric Shape Matching via Functional Maps on Landmark-Adapted Bases. In Computer Graphics Forum. Wiley Online Library.
29. Jing Ren, Simone Melzi, Peter Wonka, and Maks Ovsjanikov. 2021. Discrete optimization for shape matching. In Computer Graphics Forum, Vol. 40. Wiley, 81–96.
30. Jing Ren, Adrien Poulenard, Peter Wonka, and Maks Ovsjanikov. 2018. Continuous and orientation-preserving correspondences via functional maps. ACM Transactions on Graphics (TOG) 37, 6 (2018), 1–16.
31. Raif M Rustamov, Maks Ovsjanikov, Omri Azencot, Mirela Ben-Chen, Frédéric Chazal, and Leonidas Guibas. 2013. Map-based exploration of intrinsic shape differences and variability. ACM Transactions on Graphics (TOG) 32, 4 (2013), 1–12.
32. Yusuf Sahillioglu. 2020. Recent advances in shape correspondence. The Visual Computer 36, 8 (2020), 1705–1721.
33. Matan Sela, Yonathan Aflalo, and Ron Kimmel. 2015. Computational Caricaturization of Surfaces. Comput. Vis. Image Underst. 141, C (dec 2015), 1–17. https://doi.org/10.1016/j.cviu.2015.05.013
34. Yu Wang, Mirela Ben-Chen, Iosif Polterovich, and Justin Solomon. 2018. Steklov spectral geometry for extrinsic shape analysis. ACM Transactions on Graphics (TOG) 38, 1 (2018), 1–21.
35. Benedikt Wirth, Leah Bar, Martin Rumpf, and Guillermo Sapiro. 2011. A continuum mechanical approach to geodesics in shape space. International Journal of Computer Vision 93, 3 (2011), 293–318.
36. Dong-Ming Yan, Guanbo Bao, Xiaopeng Zhang, and Peter Wonka. 2014. Low-Resolution Remeshing Using the Localized Restricted Voronoi Diagram. IEEE Transactions on Visualization and Computer Graphics 20, 10 (2014), 1418–1427. https://doi.org/10.1109/TVCG.2014.2330574