“An efficient computation of handle and tunnel loops via Reeb graphs” by Dey, Fan and Wang
Conference:
Type(s):
Title:
- An efficient computation of handle and tunnel loops via Reeb graphs
Session/Category Title: Geometry & Topology
Presenter(s)/Author(s):
Moderator(s):
Abstract:
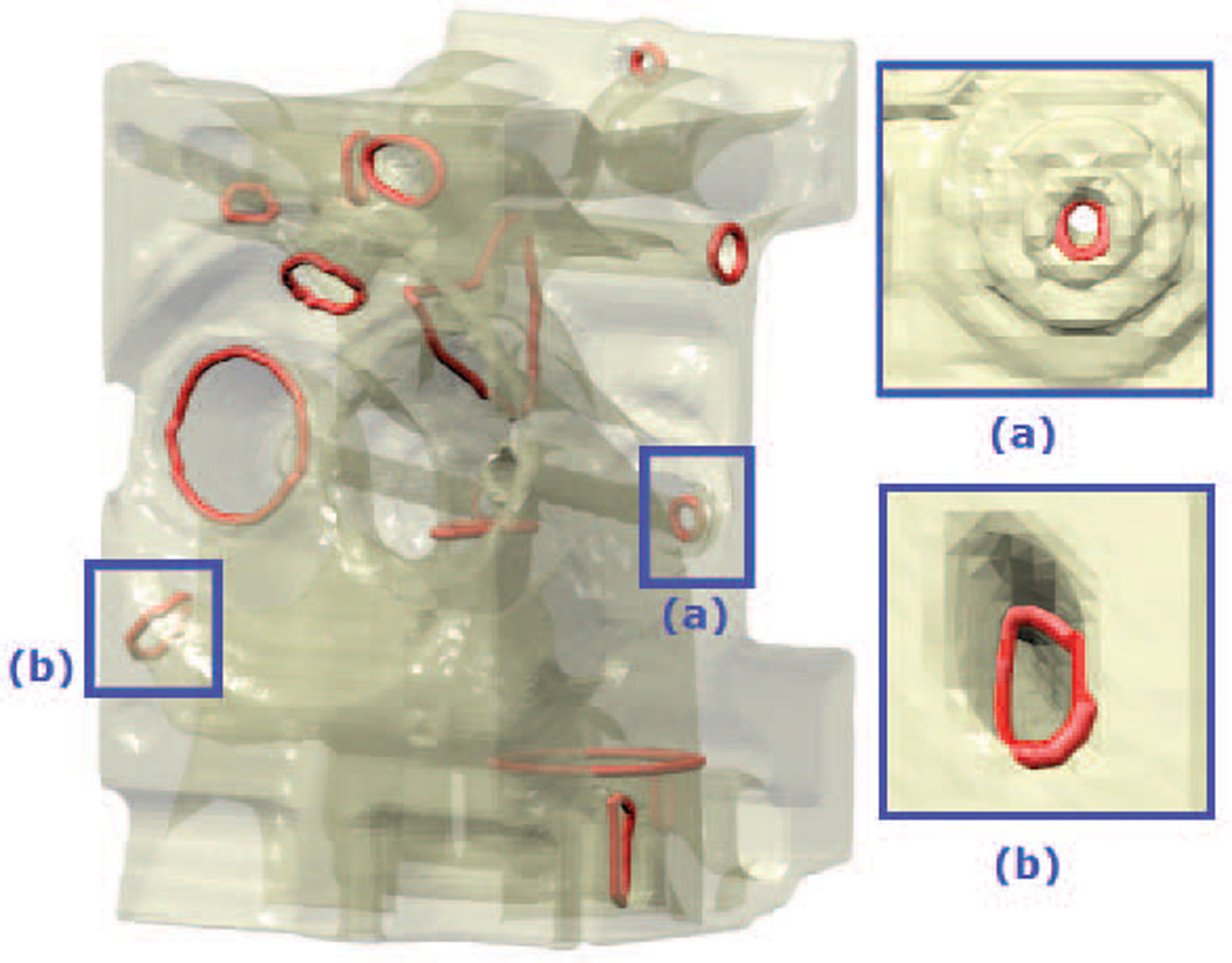
A special family of non-trivial loops on a surface called handle and tunnel loops associates closely to geometric features of “handles” and “tunnels” respectively in a 3D model. The identification of these handle and tunnel loops can benefit a broad range of applications from topology simplification/repair, and surface parameterization, to feature and shape recognition. Many of the existing efficient algorithms for computing non-trivial loops cannot be used to compute these special type of loops. The two algorithms known for computing handle and tunnel loops provably have a serious drawback that they both require a tessellation of the interior and exterior spaces bounded by the surface. Computing such a tessellation of three dimensional space around the surface is a non-trivial task and can be quite expensive. Furthermore, such a tessellation may need to refine the surface mesh, thus causing the undesirable side-effect of outputting the loops on an altered surface mesh.In this paper, we present an efficient algorithm to compute a basis for handle and tunnel loops without requiring any 3D tessellation. This saves time considerably for large meshes making the algorithm scalable while computing the loops on the original input mesh and not on some refined version of it. We use the concept of the Reeb graph which together with several key theoretical insights on linking number provide an initial set of loops that provably constitute a handle and a tunnel basis. We further develop a novel strategy to tighten these handle and tunnel basis loops to make them geometrically relevant. We demonstrate the efficiency and effectiveness of our algorithm as well as show its robustness against noise, and other anomalies in the input.
References:
1. Alliez, P., Cohen-Steiner, D., Yvinec, M., and Desbrun, M. 2005. Variational tetrahedral meshing. In Proc. SIGGRAPH 2005, 617–625. Google ScholarDigital Library
2. Ben-Chen, M., Gotsman, C., and Bunin, G. 2008. Conformal flattening by curvature prescription and metric scaling. Computer Graphics Forum (Proc. Eurographics) 27.Google Scholar
3. Biasotti, S., Giorgi, D., Spagnuolo, M., and Falcidieno, B. 2008. Reeb graphs for shape analysis and applications. Theor. Comput. Sci. 392, 1–3, 5–22. Google ScholarDigital Library
4. Bischoff, S., and Kobbelt, L. 2005. Structure preserving CAD model repair. Comput. Graphics Forum 24, 527–536.Google ScholarCross Ref
5. Busaryev, O., Cabello, S., Chen, C., Dey, T. K., and Wang, Y. 2012. Annotating simplicies with a homology basis and its applications. In SWAT, 189–200. Google ScholarDigital Library
6. Cabello, S., Colin de Verdière, É., and Lazarus, F. 2011. Finding cycles with topological properties in embedded graphs. SIAM J. Discret. Math. 25, 4, 1600–1614. Google ScholarDigital Library
7. Chambers, E. W., Erickson, J., and Nayyeri, A. 2009. Minimum cuts and shortest homologous cycles. In Proc. ACM Sympos. Comput. Geom., 377–385. Google ScholarDigital Library
8. Cheng, S.-W., Dey, T. K., and Shewchuk, J. R. 2012. Delaunay Mesh Generation. CRC Press, Boca Raton, Florida. Google ScholarDigital Library
9. Cole-McLaughlin, K., Edelsbrunner, H., Harer, J., Natarajan, V., and Pascucci, V. 2004. Loops in reeb graphs of 2-manifolds. Discrete Comput. Geom. 32, 231–244. Google ScholarDigital Library
10. Colin de Verdière, É., and Erickson, J. 2006. Tightening non-simple paths and cycles on surfaces. In Proc. ACM-SIAM Sympos. Discrete Algorithms, 192–201. Google ScholarDigital Library
11. Dey, T. K., Li, K., and Sun, J. 2007. On computing handle and tunnel loops. In Proceedings of the 2007 International Conference on Cyberworlds, CW ’07, 357–366. Google ScholarDigital Library
12. Dey, T. K., Li, K., Sun, J., and Cohen-Steiner, D. 2008. Computing geometry-aware handle and tunnel loops in 3d models. In ACM SIGGRAPH’08, 45:1–45:9. Google ScholarDigital Library
13. Dey, T. K., Sun, J., and Wang, Y. 2011. Approximating cycles in a shortest basis of the first homology group from point data. Inverse Problems 27.Google Scholar
14. Doraiswamy, H., and Natarajan, V. 2009. Efficient algorithms for computing Reeb graphs. Computational Geometry: Theory and Applications 42, 606–616. Google ScholarDigital Library
15. El-Sana, J., and Varshney, A. 1997. Controlled simplification of genus for polygonal models. In Proc. IEEE Visualization, 403–412. Google ScholarDigital Library
16. Erickson, J., and Nayyeri, A. 2011. Minimum cuts and shortest non-separating cycles via homology covers. In Proceedings of the Twenty-Second Annual ACM-SIAM Symposium on Discrete Algorithms, SODA ’11, 1166–1176. Google ScholarDigital Library
17. Erickson, J., and Whittlesey, K. 2005. Greedy optimal homotopy and homology generators. In Proceedings of the 16th Annual ACM-SIAM Symposium on Discrete Algorithms (SODA), 1038–1046. Google ScholarDigital Library
18. Gu, X., Gortler, S., and Hoppe, H. 2002. Geometry images. In Proc. SIGGRAPH 2002, 355–361. Google ScholarDigital Library
19. Guillemin, V., and Pollack, A. 2010. Differential Topology. American Mathematical Society.Google Scholar
20. Guskov, I., and Wood, Z. 2001. Topological noise removal. In Proc. Graphics Interface 2001, 19–26. Google ScholarDigital Library
21. Harvey, W., Wang, Y., and Wenger, R. 2010. A randomized O(m logm) time algorithm for computing reeb graph of arbitrary simplicial complexes. In Proc. 26th. Annu. Sympos. Comput. Geom., 267–276. Google ScholarDigital Library
22. Kutz, M. 2006. Computing shortest non-trivial cycles on orientable surfaces of bounded genus in almost linear time. In Proc. 22nd Annu. Sympos. Comput. Geom., 430–438. Google ScholarDigital Library
23. Munkres, J. R. 1996. Elements of Algebraic Topology. Westview Press.Google Scholar
24. Parsa, S. 2012. A deterministic O(mlogm) time algorithm for the Reeb graph. In ACM Sympos. Comput. Geom. (SoCG), 269–276. Google ScholarDigital Library
25. Pascucci, V., Scorzelli, G., Bremer, P.-T., and Mascarenhas, A. 2007. Robust on-line computation of Reeb graphs: simplicity and speed. ACM Trans. Graph. 26, 3, 58. Google ScholarDigital Library
26. Rolfsen, D. 1976. Knots and Links. Publish or Perish.Google Scholar
27. Shattuck, D. W., and Leahy, R. M. 2001. Automated graph-based analysis and correction of cortical volume topology. IEEE Trans. Med. Imaging 20, 1167–1177.Google ScholarCross Ref
28. Sheffer, A., and Hart, J. 2002. Seamster: inconspicuous low-distortion texture seam layout. In Proc. IEEE Visualization, 291–298. Google ScholarDigital Library
29. Tierny, J., Gyulassy, A., Simon, E., and Pascucci, V. 2009. Loop surgery for volumetric meshes: Reeb graphs reduced to contour trees. IEEE Trans. Vis. Comput. Graph. 15, 6, 1177–1184. Google ScholarDigital Library
30. van Kaick, O., Zhang, H., Hamarneh, G., and Cohen-Or, D. 2010. A survey on shape correspondence. In Proc. of Eurographics State-of-the-art Report, 1–22.Google Scholar
31. Wood, Z., Hoppe, H., Desbrun, M., and Schröder, P. 2004. Removing excess topology from isosurfaces. ACM Trans. Graphics 23, 511–533. Google ScholarDigital Library
32. Zhou, Q.-Y., Ju, T., and Hu, S.-M. 2007. Topology repair of solid models using skeletons. IEEE Trans. Vis. Comput. Graph. 13, 675–685. Google ScholarDigital Library