“An asymptotic numerical method for inverse elastic shape design” by Chen, Zheng, Xu and Zhou
Conference:
Type(s):
Title:
- An asymptotic numerical method for inverse elastic shape design
Session/Category Title: Fabrication
Presenter(s)/Author(s):
Moderator(s):
Abstract:
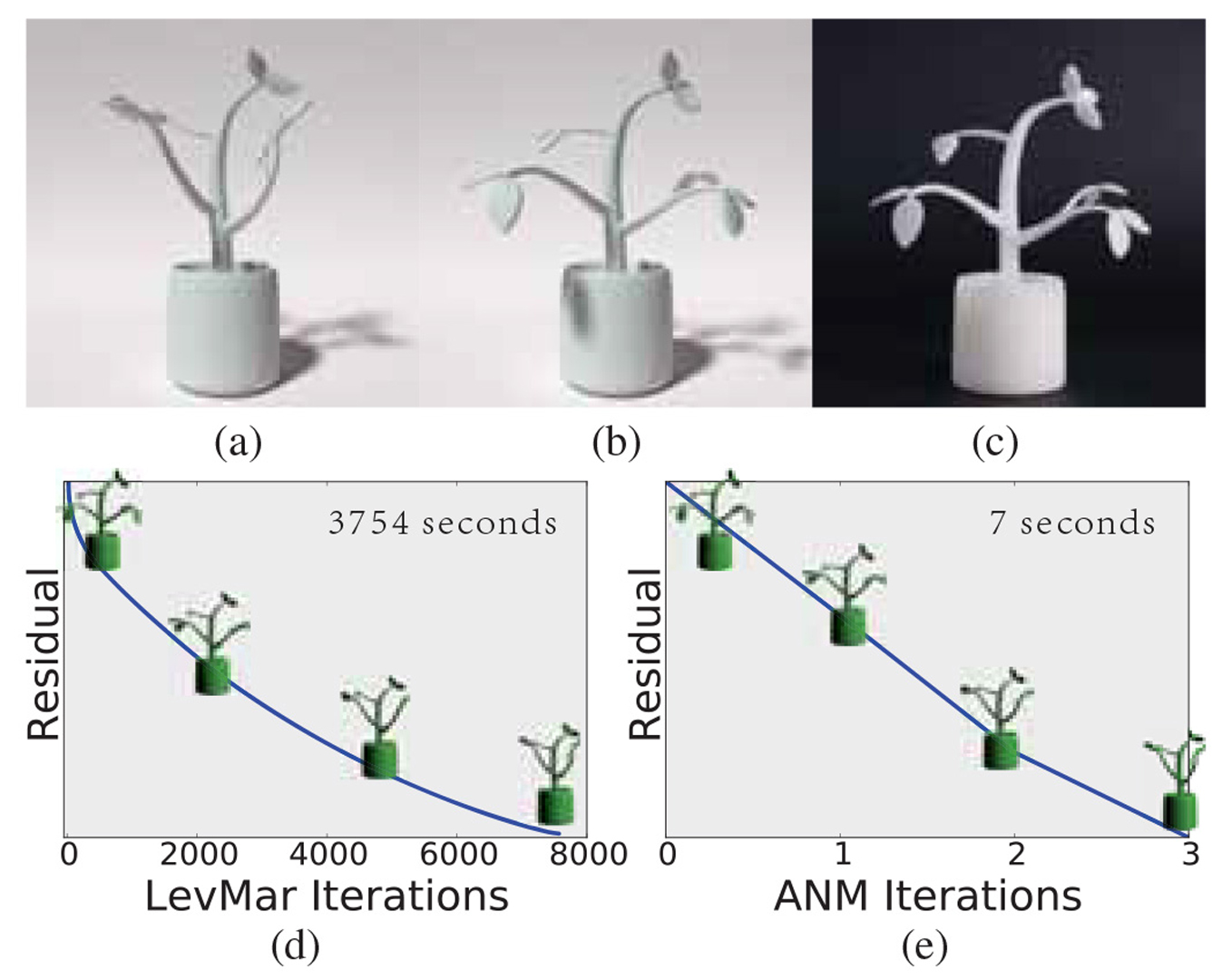
Inverse shape design for elastic objects greatly eases the design efforts by letting users focus on desired target shapes without thinking about elastic deformations. Solving this problem using classic iterative methods (e.g., Newton-Raphson methods), however, often suffers from slow convergence toward a desired solution. In this paper, we propose an asymptotic numerical method that exploits the underlying mathematical structure of specific nonlinear material models, and thus runs orders of magnitude faster than traditional Newton-type methods. We apply this method to compute rest shapes for elastic fabrication, where the rest shape of an elastic object is computed such that after physical fabrication the real object deforms into a desired shape. We illustrate the performance and robustness of our method through a series of elastic fabrication experiments.
References:
1. Allgower, E. L., and Georg, K. 1990. Numerical continuation methods, vol. 13. Springer-Verlag Berlin. Google ScholarDigital Library
2. Bächer, M., Bickel, B., James, D. L., and Pfister, H. 2012. Fabricating articulated characters from skinned meshes. ACM Trans. Graph. 31, 4, 47. Google ScholarDigital Library
3. Barbič, J., da Silva, M., and Popović, J. 2009. Deformable object animation using reduced optimal control. ACM Trans. Graph. 28, 3, 53. Google ScholarDigital Library
4. Barbič, J., Sin, F. S., and Schroeder, D., 2012. Vega FEM Library. http://www.jernejbarbic.com/vega.Google Scholar
5. Barbič, J., Sin, F., and Grinspun, E. 2012. Interactive Editing of Deformable Simulations. ACM Trans. Graph. 31, 4, 70. Google ScholarDigital Library
6. Bickel, B., Bächer, M., Otaduy, M. A., Lee, H. R., Pfister, H., Gross, M., and Matusik, W. 2010. Design and fabrication of materials with desired deformation behavior. ACM Trans. Graph. 29, 4, 63. Google ScholarDigital Library
7. Bickel, B., Kaufmann, P., Skouras, M., Thomaszewski, B., Bradley, D., Beeler, T., Jackson, P., Marschner, S., Matusik, W., and Gross, M. 2012. Physical face cloning. ACM Trans. Graph. 31, 4, 118. Google ScholarDigital Library
8. Bonet, J., and Wood, R. D. 1997. Nonlinear Continuum Mechanics for Finite Element Analysis. Cambridge University.Google Scholar
9. Brent, R. P. 2013. Algorithms for minimization without derivatives. Courier Dover Publications.Google Scholar
10. Calì, J., Calian, D. A., Amati, C., Kleinberger, R., Steed, A., Kautz, J., and Weyrich, T. 2012. 3d-printing of non-assembly, articulated models. ACM Trans. Graph. 31, 6, 130. Google ScholarDigital Library
11. Ceylan, D., Li, W., Mitra, N. J., Agrawala, M., and Pauly, M. 2013. Designing and fabricating mechanical automata from mocap sequences. ACM Trans. Graph. 32, 6, 186. Google ScholarDigital Library
12. Chen, D., Levin, D. I. W., Didyk, P., Sitthi-Amorn, P., and Matusik, W. 2013. Spec2fab: A reducer-tuner model for translating specifications to 3d prints. ACM Trans. Graph. 32, 4. Google ScholarDigital Library
13. Cochelin, B. 1994. A path-following technique via an asymptotic-numerical method. Computers & structures 53, 5, 1181–1192.Google Scholar
14. Coros, S., Martin, S., Thomaszewski, B., Schumacher, C., Sumner, R., and Gross, M. 2012. Deformable objects alive! ACM Trans. Graph. 31, 4, 69. Google ScholarDigital Library
15. Coros, S., Thomaszewski, B., Noris, G., Sueda, S., Forberg, M., Sumner, R. W., Matusik, W., and Bickel, B. 2013. Computational design of mechanical characters. ACM Trans. Graph. 32, 4, 83. Google ScholarDigital Library
16. Damil, N., and Potier-Ferry, M. 1990. A new method to compute perturbed bifurcations: Application to the buckling of imperfect elastic structures. International Journal of Engineering Science 28, 9, 943–957.Google ScholarCross Ref
17. Derouet-Jourdan, A., Bertails-Descoubes, F., and Thollot, J. 2010. Stable inverse dynamic curves. ACM Trans. Graph. 29, 6, 137. Google ScholarDigital Library
18. Derouet-Jourdan, A., Bertails-Descoubes, F., Daviet, G., and Thollot, J. 2013. Inverse dynamic hair modeling with frictional contact. ACM Trans. Graph. 32, 6, 159. Google ScholarDigital Library
19. Hadap, S. 2006. Oriented strands: dynamics of stiff multi-body system. In Proceedings of SCA, 91–100. Google ScholarDigital Library
20. Hildebrandt, K., Schulz, C., von Tycowicz, C., and Polthier, K. 2012. Interactive spacetime control of deformable objects. ACM Trans. Graph. 31, 4, 71. Google ScholarDigital Library
21. Lazarus, A., Miller, J., and Reis, P. 2013. Continuation of equilibria and stability of slender elastic rods using an asymptotic numerical method. J. Mech. Phys. Solids 61, 8, 1712–1736.Google ScholarCross Ref
22. Levenberg, K. 1944. A method for the solution of certain nonlinear problems in least squares. Quart. J. Appl. Maths. II, 2.Google Scholar
23. Lourakis, M. I. A., Jul. 2004. levmar: Levenberg-marquardt nonlinear least squares algorithms in C/C++. {web page} http://www.ics.forth.gr/~lourakis/levmar.Google Scholar
24. Martin, S., Thomaszewski, B., Grinspun, E., and Gross, M. 2011. Example-based elastic materials. ACM Trans. Graph. 30, 4, 72. Google ScholarDigital Library
25. Miguel, E., Bradley, D., Thomaszewski, B., Bickel, B., Matusik, W., Otaduy, M. A., and Marschner, S. 2012. Data-driven estimation of cloth simulation models. Computer Graphics Forum 31, 2, 519–528. Google ScholarDigital Library
26. Nealen, A., Müller, M., Keiser, R., Boxerman, E., and Carlson, M. 2006. Physically based deformable models in computer graphics. Computer Graphics Forum 25, 4, 809–836.Google ScholarCross Ref
27. Ogden, R. W. 1997. Non-linear elastic deformations. Courier Dover Publications.Google Scholar
28. Prévost, R., Whiting, E., Lefebvre, S., and Sorkine-Hornung, O. 2013. Make it stand: balancing shapes for 3d fabrication. ACM Trans. Graph. 32, 4, 81. Google ScholarDigital Library
29. Skouras, M., Thomaszewski, B., Bickel, B., and Gross, M. 2012. Computational design of rubber balloons. Computer Graphics Forum 31, 2, 835–844. Google ScholarDigital Library
30. Skouras, M., Thomaszewski, B., Coros, S., Bickel, B., and Gross, M. 2013. Computational design of actuated deformable characters. ACM Trans. Graph. 32, 4, 82. Google ScholarDigital Library
31. Stava, O., Vanek, J., Benes, B., Carr, N., and Měch, R. 2012. Stress relief: Improving structural strength of 3d printable objects. ACM Trans. Graph. 31, 4, 48. Google ScholarDigital Library
32. SunPe, P. Professional Rapid Prototyping & Manufacturing. http://www.sunpe.com/types-34.html, SunPe PROTOTYPE.Google Scholar
33. Twigg, C. D., and Kačić-Alesić, Z. 2011. Optimization for sag-free simulations. In Proceedings of SCA, 225–236. Google ScholarDigital Library
34. Umetani, N., Kaufman, D. M., Igarashi, T., and Grinspun, E. 2011. Sensitive couture for interactive garment modeling and editing. ACM Trans. Graph. 30, 4, 90. Google ScholarDigital Library
35. Zahrouni, H., Cochelin, B., and Potier-Ferry, M. 1999. Computing finite rotations of shells by an asymptotic-numerical method. Comput. Methods Appl. Mech. Eng. 175, 1, 71–85.Google ScholarCross Ref