“An advection-reflection solver for detail-preserving fluid simulation” by Zehnder, Narain and Thomaszewski
Conference:
Type(s):
Entry Number: 85
Title:
- An advection-reflection solver for detail-preserving fluid simulation
Session/Category Title: Fluids 1: Raiders of the Lost Volume
Presenter(s)/Author(s):
Moderator(s):
Abstract:
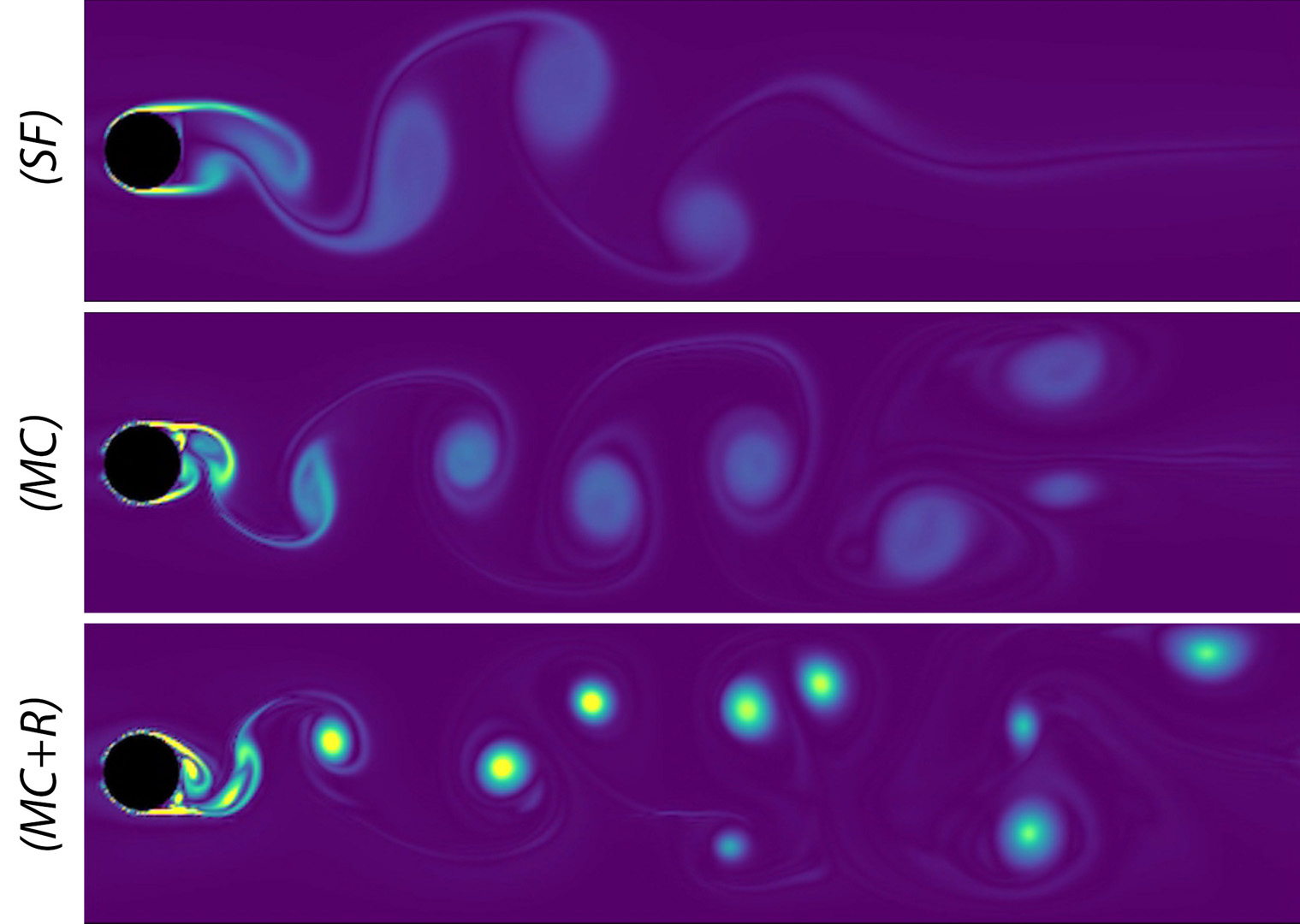
Advection-projection methods for fluid animation are widely appreciated for their stability and efficiency. However, the projection step dissipates energy from the system, leading to artificial viscosity and suppression of small-scale details. We propose an alternative approach for detail-preserving fluid animation that is surprisingly simple and effective. We replace the energy-dissipating projection operator applied at the end of a simulation step by an energy-preserving reflection operator applied at mid-step. We show that doing so leads to two orders of magnitude reduction in energy loss, which in turn yields vastly improved detail-preservation. We evaluate our reflection solver on a set of 2D and 3D numerical experiments and show that it compares favorably to state-of-the-art methods. Finally, our method integrates seamlessly with existing projection-advection solvers and requires very little additional implementation.
References:
1. Alexis Angelidis and Fabrice Neyret. 2005. Simulation of Smoke Based on Vortex Filament Primitives. In Proceedings of the 2005 ACM SIGGRAPH/Eurographics Symposium on Computer Animation (SCA ’05). 87–96. Google ScholarDigital Library
2. Christopher Batty, Florence Bertails, and Robert Bridson. 2007. A Fast Variational Framework for Accurate Solid-fluid Coupling. ACM Trans. Graph. 26, 3 (July 2007). Google ScholarDigital Library
3. Albert Chern, Felix Knöppel, Ulrich Pinkall, Peter Schröder, and Steffen Weißmann. 2016. Schrödinger’s Smoke. ACM Trans. Graph. 35, 4 (July 2016), 77:1–77:13.Google ScholarDigital Library
4. Alexandre Joel Chorin. 1968. Numerical solution of the Navier-Stokes equations. Math. Comp. 22 (1968), 745–762.Google ScholarCross Ref
5. Sharif Elcott, Yiying Tong, Eva Kanso, Peter Schröder, and Mathieu Desbrun. 2007. Stable, Circulation-preserving, Simplicial Fluids. ACM Trans. Graph. 26, 1 (Jan. 2007). Google ScholarDigital Library
6. Ronald Fedkiw, Jos Stam, and Henrik Wann Jensen. 2001. Visual Simulation of Smoke. In Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques (SIGGRAPH ’01). 15–22. Google ScholarDigital Library
7. Nick Foster and Dimitri Metaxas. 1996. Realistic Animation of Liquids. Graphical Models and Image Processing 58, 5 (Sept. 1996), 471 — 483. Google ScholarDigital Library
8. Rony Goldenthal, David Harmon, Raanan Fattal, Michel Bercovier, and Eitan Grinspun. 2007. Efficient Simulation of Inextensible Cloth. ACM Trans. Graph. 26, 3 (July 2007). Google ScholarDigital Library
9. Ernst Hairer, Christian Lubich, and Gerhard Wanner. 2006. Geometric Numerical Integration: Structure-Preserving Algorithms for Ordinary Differential Equations; 2nd ed. Springer, Dordrecht. https://cds.cern.ch/record/1250576Google Scholar
10. Francis H. Harlow and J. Eddie Welch. 1965. Numerical Calculation of Time-Dependent Viscous Incompressible Flow of Fluid with Free Surface. The Physics of Fluids 8, 12 (1965), 2182–2189.Google ScholarCross Ref
11. Markus Ihmsen, Jens Orthmann, Barbara Solenthaler, Andreas Kolb, and Matthias Teschner. 2014. SPH Fluids in Computer Graphics. In Eurographics 2014 – State of the Art Reports.Google Scholar
12. Geoffrey Irving, Craig Schroeder, and Ronald Fedkiw. 2007. Volume Conserving Finite Element Simulations of Deformable Models. ACM Trans. Graph. 26, 3 (July 2007). Google ScholarDigital Library
13. Chenfanfu Jiang, Craig Schroeder, Andrew Selle, Joseph Teran, and Alexey Stomakhin. 2015. The affine particle-in-cell method. ACM Transactions on Graphics (TOG) 34, 4 (July 2015), 51:1–51:10. Google ScholarDigital Library
14. ByungMoon Kim, Yingjie Liu, Ignacio Llamas, and Jarek Rossignac. 2005. FlowFixer: Using BFECC for Fluid Simulation. In Proceedings of the First Eurographics Conference on Natural Phenomena (NPH’05). 51–56. Google ScholarDigital Library
15. ByungMoon Kim, Yingjie Liu, Ignacio Llamas, and Jarek Rossignac. 2007. Advections with Significantly Reduced Dissipation and Diffusion. IEEE Transactions on Visualization and Computer Graphics 13, 1 (Jan. 2007), 135–144. Google ScholarDigital Library
16. Doyub Kim, Oh-young Song, and Hyeong-Seok Ko. 2008a. A Semi-Lagrangian CIP Fluid Solver without Dimensional Splitting. Computer Graphics Forum 27, 2 (April 2008), 467–475.Google ScholarCross Ref
17. Theodore Kim, Nils Thürey, Doug James, and Markus Gross. 2008b. Wavelet Turbulence for Fluid Simulation. ACM Trans. Graph. 27, 3 (Aug. 2008), 50:1–50:6. Google ScholarDigital Library
18. B.P. Leonard. 1979. A stable and accurate convective modelling procedure based on quadratic upstream interpolation. Computer Methods in Applied Mechanics and Engineering 19, 1 (1979), 59 — 98. Google ScholarDigital Library
19. Jeroen Molemaker, Jonathan M. Cohen, Sanjit Patel, and Junyong Noh. 2008. Low Viscosity Flow Simulations for Animation. In SCA ’08: Proceedings of the 2007 ACM SIGGRAPH/Eurographics Symposium on Computer Animation. 9–18. Google ScholarDigital Library
20. Patrick Mullen, Keenan Crane, Dmitry Pavlov, Yiying Tong, and Mathieu Desbrun. 2009. Energy-preserving Integrators for Fluid Animation. ACM Trans. Graph. 28, 3 (July 2009), 38:1–38:8. Google ScholarDigital Library
21. Sang Il Park and Myoung Jun Kim. 2005. Vortex Fluid for Gaseous Phenomena. In Proceedings of the 2005 ACM SIGGRAPH/Eurographics Symposium on Computer Animation (SCA ’05). 261–270. Google ScholarDigital Library
22. André Robert. 1981. A stable numerical integration scheme for the primitive meteorological equations. Atmosphere-Ocean 19, 1 (1981), 35–46.Google ScholarCross Ref
23. Andrew Selle, Ronald Fedkiw, Byungmoon Kim, Yingjie Liu, and Jarek Rossignac. 2008. An Unconditionally Stable MacCormack Method. J. Sci. Comput. 35, 2-3 (June 2008), 350–371. Google ScholarDigital Library
24. Andrew Selle, Nick Rasmussen, and Ronald Fedkiw. 2005. A vortex particle method for smoke, water and explosions. ACM Transactions on Graphics (TOG) 24, 3 (July 2005), 910–914. Google ScholarDigital Library
25. Jos Stam. 1999. Stable fluids. In Proceedings of the 26th annual conference on Computer graphics and interactive techniques. 121–128. Google ScholarDigital Library
26. Nils Thuerey, Theodore Kim, and Tobias Pfaff. 2013. Turbulent fluids. In ACM SIGGRAPH 2013 Courses. ACM, 6. Google ScholarDigital Library
27. Nils Thuerey and Tobias Pfaff. 2016. Mantaflow. http://mantaflow.com. (2016).Google Scholar
28. Steffen Weißmann and Ulrich Pinkall. 2010. Filament-based Smoke with Vortex Shedding and Variational Reconnection. ACM Trans. Graph. 29, 4 (July 2010), 115:1–115:12. Google ScholarDigital Library
29. Xinxin Zhang, Robert Bridson, and Chen Greif. 2015. Restoring the Missing Vorticity in Advection-projection Fluid Solvers. ACM Trans. Graph. 34, 4 (July 2015), 52:1–52:8. Google ScholarDigital Library
30. Yongning Zhu and Robert Bridson. 2005. Animating Sand as a Fluid. 24 (July 2005), 965–972. Google ScholarDigital Library