“All’s well that ends well: guaranteed resolution of simultaneous rigid body impact” by Montanari, Petrinic and Barbieri
Conference:
Type(s):
Title:
- All's well that ends well: guaranteed resolution of simultaneous rigid body impact
Session/Category Title: Let's Get in Contact
Presenter(s)/Author(s):
Moderator(s):
Abstract:
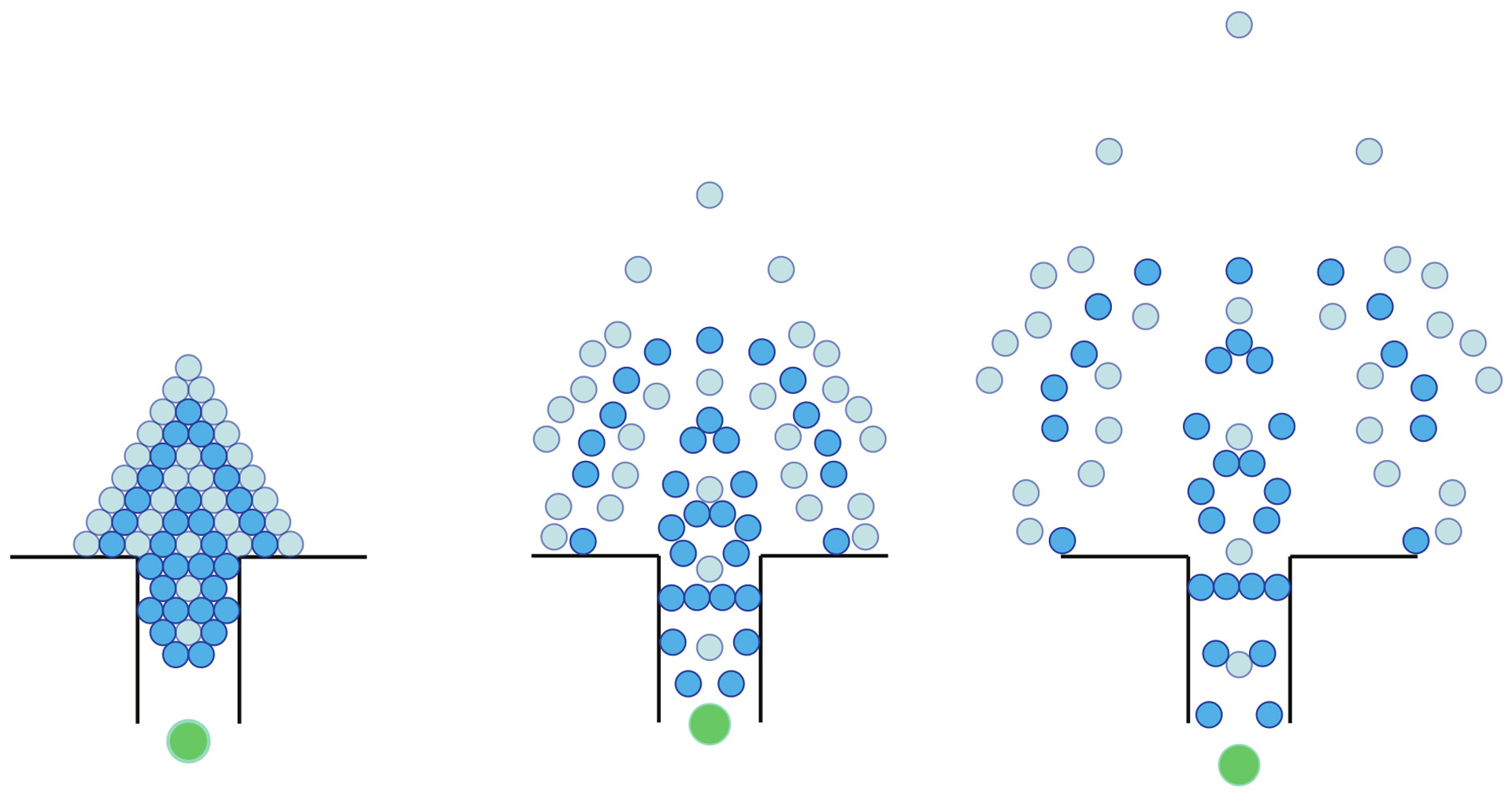
Iterative algorithms are frequently used to resolve simultaneous impacts between rigid bodies in physical simulations. However, these algorithms lack formal guarantees of termination, which is sometimes viewed as potentially dangerous, so failsafes are used in practical codes to prevent infinite loops. We show such steps are unnecessary. In particular, we study the broad class of such algorithms that are conservative and satisfy a minimal set of physical correctness properties, and which encompasses recent methods like Generalized Reflections as well as pairwise schemes. We fully characterize finite termination of these algorithms. The only possible failure cases can be detected, and we describe a procedure for modifying the algorithms to provably ensure termination. We also describe modifications necessary to guarantee termination in the presence of numerical error due to the use of floating-point arithmetic. Finally, we discuss the challenges dissipation introduce for finite termination, and describe how dissipation models can be incorporated while retaining the termination guarantee.
References:
1. Mihai Anitescu and Florian R. Potra. 1997. Formulating Dynamic Multi-Rigid-Body Contact Problems with Friction as Solvable Linear Complementarity Problems. Nonlinear Dynamics 14, 3 (1997), 231–247. Google ScholarCross Ref
2. David Baraff. 1989. Analytical Methods for Dynamic Simulation of Non-penetrating Rigid Bodies. In Proceedings of the 16th Annual Conference on Computer Graphics and Interactive Techniques (SIGGRAPH ’89). ACM, New York, NY, USA, 223–232. Google ScholarDigital Library
3. Jan Bender, Kenny Erleben, and Jeff Trinkle. 2014. Interactive Simulation of Rigid Body Dynamics in Computer Graphics. Computer Graphics Forum 33 (2014), 246–270. Issue 1.Google ScholarDigital Library
4. B. Bernu and R. Mazighi. 1990. One-Dimensional Bounce of Inelastically Colliding Marbles on a Wall. Journal of Physics A: Mathematical and General 23, 24 (1990), 5745–5754. Google ScholarCross Ref
5. Bernard Brogliato. 1999. Nonsmooth Mechanics: models, dynamics, and control (2nd ed.). Springer-Verlag. Google ScholarCross Ref
6. Mario E. Caire, Francisco J. López, and David H. Williams. 2008. Distributed identification of the lineality space of a cone. The Journal of Supercomputing 48, 2 (2008), 163–182. Google ScholarDigital Library
7. A. Chatterjee and A. L. Ruina. 1998. A New Algebraic Rigid-Body Collision Law Based on Impulse Space Considerations. Journal of Applied Mechanics 65, 4 (1998), 939–951. Google ScholarCross Ref
8. Richard W. Cottle, Jong Shi Pang, and Richard E. Stone. 1992. The Linear Complementarity Problem. Academic Press, New York.Google Scholar
9. J. Crassous, D. Beladjine, and A.Valance. 2007. Impact of a Projectile on a Granular Medium Described by a Collision Model. Physical Review Letters 99 (2007), 248001. Google ScholarCross Ref
10. J. d’Alembert. 1743. Traité de Dynamique. Paris.Google Scholar
11. J. R. de Felicio and D. M. Redondo. 1981. Linear collisions revisited. Am. J. Phys 49, 147 (1981). Google ScholarCross Ref
12. A. Donev, I. Cisse, D. Sachs, E.A. Variano, F.H. Stillinger, R. Connelly, S. Torquato, and P.M. Chaikin. 2004. Improving the density of jammed disordered packings using ellipsoids. Science 303 (2004), 990–993. Google ScholarCross Ref
13. E. Drumwright and D. Shell. 2011. Modeling contact friction and joint friction in dynamic robotic simulation using the principle of maximum dissipation. Springer Berlin Heidelberg, 249–266.Google Scholar
14. Jeff Erickson and Scott Kim. 2003. Arbitrarily Large Neighborly Families of Congruent Symmetric Convex 3-Polytopes. CRC Press.Google Scholar
15. Kenny Erleben. 2007. Velocity-based Shock Propagation for Multibody Dynamics Animation. ACM Trans. Graph. 26, 2, Article 12 (June 2007), 12:1–12:20 pages. Google ScholarDigital Library
16. G. Gilardi and I. Sharf. 2002. Literature survey of contact dynamics modelling. Mechanism and Machine Theory 37 (2002), 1213–1239. Issue 10.Google ScholarCross Ref
17. Christof Glocker. 2004. Concepts for Modeling Impacts without Friction. Acta Mechanica 168 (2004), 1–19. Google ScholarCross Ref
18. Suresh Goyal, Andy Ruina, and Jim Papadopoulos. 1991. Planar sliding with dry friction, Part 1. Limit surface and moment function. Wear 143 (1991), 307–330. Google ScholarCross Ref
19. I. Han and B. J. Gilmore. 1993. Multi-Body Impact Motion with Friction—Analysis, Simulation, and Experimental Validation. J. Mech. Des 115, 3 (1993), 412–422. Google ScholarCross Ref
20. A. P. Ivanov. 1995. On multiple impact. Journal of Applied Mathematics and Mechanics 59, 6 (1995), 887–902. Google ScholarCross Ref
21. Y.-B. Jia, M. Mason, and M. Erdmann. 2013. Multiple Impacts: A State Transition Diagram Approach. International Journal of Robotics Research 32, 1 (2013), 84–114. Google ScholarDigital Library
22. W. Johnson. 1976. Simple Linear Impact. International Journal of Mechanical Engineering Education 4, 2 (1976), 167–181.Google Scholar
23. Danny M. Kaufman, Timothy Edmunds, and Dinesh K. Pai. 2005. Fast frictional dynamics for rigid bodies. ACM TOG (SIGGRAPH 05) 24, 3 (2005), 946–956.Google Scholar
24. Y. A Khulief. 2012. Modeling of Impact in Multibody Systems: An Overview. J. Comput. Nonlinear Dynam. 8, 2 (2012), 021012. Google ScholarCross Ref
25. Caishan Liu, Zhen Zhao, and Bernard Brogliato. 2008. Frictionless Multiple Impacts in Multibody Systems. I. Theoretical Framework. Proceedings of the Royal Society A 464 (2008), 3193–3211. Google ScholarCross Ref
26. Francisco López. 2011. An Algorithm to Find the Lineality Space of the Positive Hull of a Set of Vectors. Journal of Mathematical Modelling and Algorithms 10 (2011), 1–30. Issue 1. Google ScholarDigital Library
27. Colin MacLaurin. 1742. A Treatise on Fluxions. T. W. and T. Ruddimans, Edinburgh.Google Scholar
28. Sean McNamara and W. R. Young. 1994. Inelastic collapse in two dimensions. Phys. Rev. E 50, 1 (Jul 1994), R28–R31. Google ScholarCross Ref
29. J. J. Moreau. 1985. Standard Inelastic Shocks and the Dynamics of Unilateral Constraints. In Unilateral Problems in Structural Analysis: Proceedings of the Second Meeting on Unilateral Problems in Structural Analysis, Ravello, September 22–24, 1983, Gianpietro Del Piero and Franco Maceri (Eds.). Springer Vienna, Vienna, 173–221. Google ScholarCross Ref
30. Pieter J. Mosterman. 2001. On the Normal Component of Centralized Frictionless Collision Sequences. J. Appl. Mech. 74, 5 (2001), 908–915. Google ScholarCross Ref
31. N. Nguyen and B. Brogliato. 2014. Multiple Impacts in Dissipative Granular Chains. Springer Heidelberg. Google ScholarCross Ref
32. X. Provot. 1997. Collision and Self-collision Handling in Cloth Model Dedicated to Design. In Computer Animation and Simulation ’97. 177–190. Google ScholarCross Ref
33. Breannan Smith, Danny M. Kaufman, Etienne Vouga, Rasmus Tamstorf, and Eitan Grinspun. 2012. Reflections on Simultaneous Impact. ACM Trans. Graph. 31, 4, Article 106 (July 2012), 12 pages. Google ScholarDigital Library
34. David E. Stewart. 2000. Rigid-Body Dynamics with Friction and Impact. SIAM Rev. 42, 1 (2000), 3–39. Google ScholarDigital Library
35. David E Stewart. 2011. Dynamics with Inequalities: Impacts and Hard Constraints. Society for Industrial and Applied Mathematics.Google Scholar
36. Dan Stoianovici and Yildirim Hurmuzlu. 1996. A critical study of the applicability of rigid-body collision theory. Journal of Applied Mechanics 63, 2 (1996), 307–316. Google ScholarCross Ref
37. Jan Telgen. 1983. Identifying Redundant Constraints and Implicit Equalities in Systems of Linear Constraints. Management Science 29, 10 (1983), 1209–1222. Google ScholarDigital Library
38. Albert Anton ten Dam. 1997. Unilaterally constrained dynamical systems. Ph.D. Dissertation. Rijksuniversiteit Groningen. http://hdl.handle.net/11370/0c2036b1-cab4-49e1-a602-13e417923985Google Scholar
39. T. Uchida, M. Sherman, and S. Delp. 2015. Making a meaningful impact: modelling simultaneous frictional collisions in spatial multibody systems. Proc. Math. Phys. Eng. Sci. 471, 2177 (2015), 20140859. Google ScholarCross Ref
40. Roger J.-B. Wets and Christoph Witzgall. 1967. Algorithms for Frames and Lineality Spaces of Cones. Journal of Research of the National Bureau of Standards, B Mathematics and Mathematical Physics 71B, 1 (January-March 1967), 1–7. Google ScholarCross Ref
41. A. Wouterse, S. Luding, and A. P. Philipse. 2009. On contact numbers in random rod packings. Granular Matter 11 (2009), 169–177. Google ScholarCross Ref
42. Tianxiang Zhang, Sheng Li, Guoping Wang, Dinesh Manocha, and Hanqiu Sun. 2015. Quadratic Contact Energy Model for Multi-impact Simulation. Computer Graphics Forum 34 (2015), 133–144. Issue 7.Google ScholarDigital Library