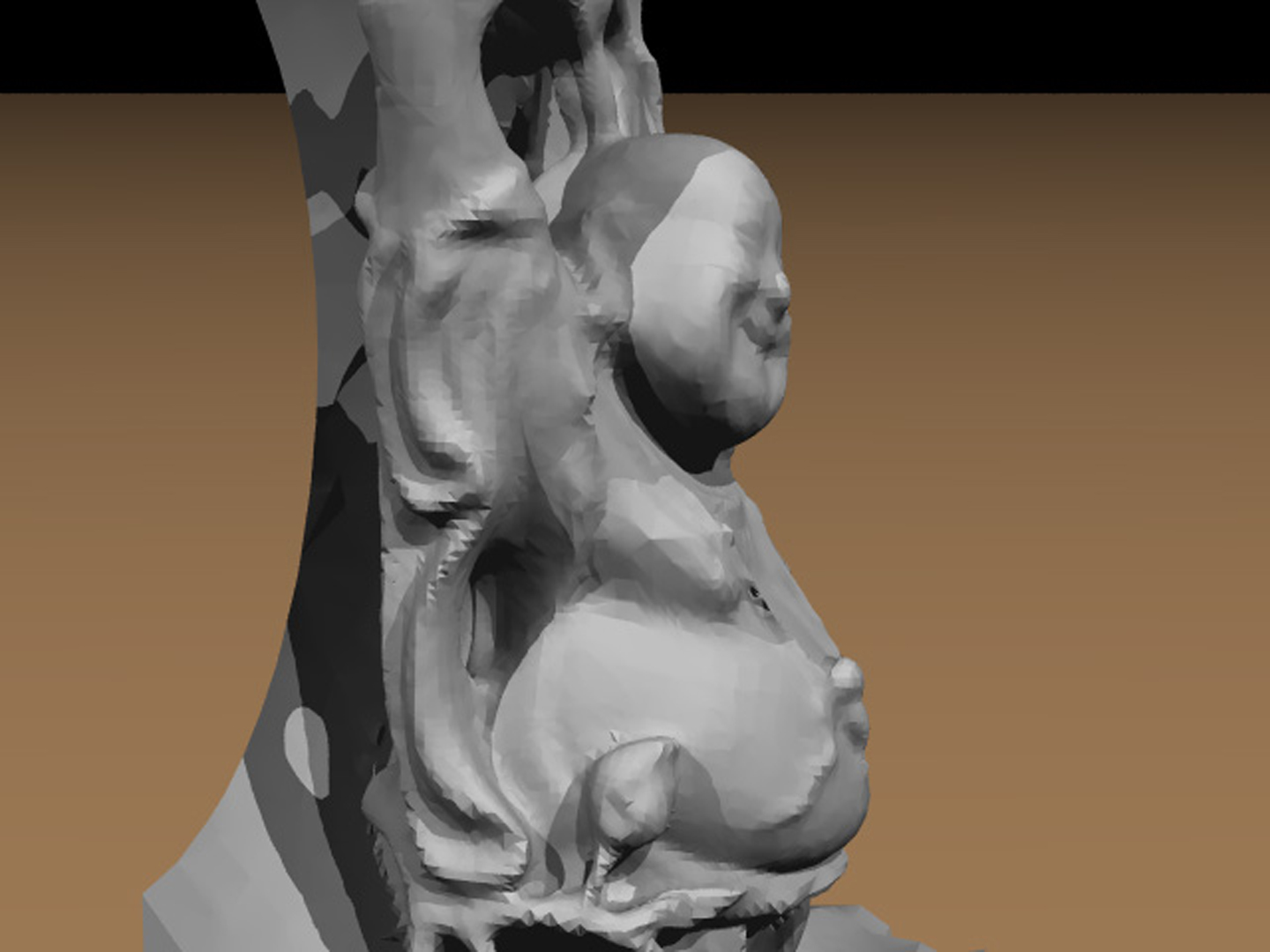
“A virtual node algorithm for changing mesh topology during simulation” by Molino, Bao and Fedkiw

We propose a virtual node algorithm that allows material to separate along arbitrary (possibly branched) piecewise linear paths through a mesh. The material within an element is fragmented by creating several replicas of the element and assigning a portion of real material to each replica. This results in elements that contain both real material and empty regions. The missing material is contained in another copy (or copies) of this element. Our new virtual node algorithm automatically determines the number of replicas and the assignment of material to each. Moreover, it provides the degrees of freedom required to simulate the partially or fully fragmented material in a fashion consistent with the embedded geometry. This approach enables efficient simulation of complex geometry with a simple mesh, i.e. the geometry need not align itself with element boundaries. It also alleviates many shortcomings of traditional Lagrangian simulation techniques for meshes with changing topology. For example, slivers do not require small CFL time step restrictions since they are embedded in well shaped larger elements. To enable robust simulation of embedded geometry, we propose new algorithms for handling rigid body and self collisions. In addition, we present several mechanisms for influencing and controlling fracture with grain boundaries, prescoring, etc. We illustrate our method for both volumetric and thin-shell simulations.

1. AIVAZIS, M., GODDARD, W., MEIRON, D., ORTIZ, M., POOL, J., AND SHEPHERD, J. 2000. A virtual test facility for simulating the dynamic response of materials. Comput. in Sci. and Eng. 2, 42–53. Google ScholarDigital Library
2. ARMERO, F., AND LOVE, E. 2003. An arbitrary lagrangian-eulerian finite element method for finite strain plasticity. Int. J. Num. Meth. Eng. 57, 471–508.Google ScholarCross Ref
3. BARAFF, D., AND WITKIN, A. 1998. Large steps in cloth simulation. In Proc. SIGGRAPH 98, 1–12. Google ScholarDigital Library
4. BARAFF, D., WITKIN, A., AND KASS, M. 2003. Untangling cloth. ACM Trans. Graph. (SIGGRAPH Proc.) 22, 862–870. Google ScholarDigital Library
5. BELYTSCHKO, T., CHEN, H., XU, J., AND ZI, G. 2003. Dynamic crack propagation based on loss of hyperbolicity and a new discontinuous enrichment. Int. J. Num. Meth. Eng. 58, 1873–1905.Google ScholarCross Ref
6. BESSETTE, G., BECKER, E., TAYLOR, L., AND LITTLEFIELD, D. 2003. Modeling of impact problems using an h-adaptive, explicit lagrangian finite element method in three dimensions. Comput. Meth. in Appl. Mech. and Eng. 192, 1649–1679.Google ScholarCross Ref
7. BIELSER, D., AND GROSS, M. 2000. Interactive simulation of surgical cuts. In Pacific Graph., 116–125. Google ScholarDigital Library
8. BIELSER, D., GLARDON, P., TESCHNER, M., AND GROSS, M. 2003. A state machine for real-time cutting of tetrahedral meshes. In Pacific Graph., 377–386. Google ScholarDigital Library
9. BOUCHARD, P., BAY, F., AND CHASTEL, Y. 2003. Numerical modelling of crack propagation: automatic remeshing and comparison of different criteria. Comput. Meth. in Appl. Mech. and Eng. 192, 3887–3908.Google ScholarCross Ref
10. BRIDSON, R., FEDKIW, R., AND ANDERSON, J. 2002. Robust treatment of collisions, contact and friction for cloth animation. ACM Trans. Graph. (SIGGRAPH Proc.) 21, 594–603. Google ScholarDigital Library
11. BRIDSON, R., MARINO, S., AND FEDKIW, R. 2003. Simulation of clothing with folds and wrinkles. In Proc. of the 2003 ACM SIGGRAPH/Eurographics Symp. on Comput. Anim., 28–36. Google ScholarDigital Library
12. CAMACHO, G., AND ORTIZ, M. 1997. Adaptive Lagrangian modelling of ballistic penetration of metallic targets. Comput. Meth. in Appl. Mech. and Eng. 142, 269–301.Google ScholarCross Ref
13. CAPELL, S., GREEN, S., CURLESS, B., DUCHAMP, T., AND POPOVIĆ, Z. 2002. Interactive skeleton-driven dynamic deformations. ACM Trans. Graph. (SIGGRAPH Proc.) 21, 586–593. Google ScholarDigital Library
14. CAPELL, S., GREEN, S., CURLESS, B., DUCHAMP, T., AND POPOVIĆ, Z. 2002. A multiresolution framework for dynamic deformations. In ACM SIGGRAPH Symp. on Comput. Anim., ACM Press, 41–48. Google ScholarDigital Library
15. CHEN, D., AND ZELTZER, D. 1992. Pump it up: Computer animation of a biomechanically based model of muscle using the finite element method. Comput. Graph. (SIGGRAPH Proc.), 89–98. Google ScholarDigital Library
16. CHOI, K.-J., AND KO, H.-S. 2002. Stable but responsive cloth. ACM Trans. Graph. (SIGGRAPH Proc.) 21, 604–611. Google ScholarDigital Library
17. CUTLER, B., DORSEY, J., MCMILLAN, L., MULLER, M., AND JAGNOW, R. 2002. A procedural approach to authoring solid models. ACM Trans. Graph. (SIGGRAPH Proc.) 21, 3, 302–311. Google ScholarDigital Library
18. DEBUNNE, G., DESBRUN, M., CANI, M., AND BARR, A. 2001. Dynamic real-time deformations using space & time adaptive sampling. In Proc. SIGGRAPH 2001, vol. 20, 31–36. Google ScholarDigital Library
19. ETZMUSS, O., KECKEISEN, M., AND STRASSER, W. 2003. A fast finite element solution for cloth modelling. In Pacific Graph., 244–251. Google ScholarDigital Library
20. FALOUTSOS, P., VANDE PANNE, M., AND TERZOPOULOS, D. 1997. Dynamic free-form deformations for animation synthesis. IEEE Trans. on Vis. and Comput. Graphics 3, 3, 201–214. Google ScholarDigital Library
21. FEDKIW, R., ASLAM, T., MERRIMAN, B., AND OSHER, S. 1999. A non-oscillatory Eulerian approach to interfaces in multimaterial flows (the ghost fluid method). J. Comput. Phys. 152, 457–492. Google ScholarDigital Library
22. FOREST, C., DELINGETTE, H., AND AYACHE, N. 2002. Removing tetrahedra from a manifold mesh. In Computer Animation, 225–229. Google ScholarDigital Library
23. GOURRET, J.-P., MAGNENAT-THALMANN, N., AND THALMANN, D. 1989. Simulation of object and human skin deformations in a grasping task. Comput. Graph. (SIGGRAPH Proc.), 21–30. Google ScholarDigital Library
24. GRINSPUN, E., KRYSL, P., AND SCHRODER, P. 2002. CHARMS: A simple framework for adaptive simulation. ACM Trans. Graph. (SIGGRAPH Proc.) 21, 281–290. Google ScholarDigital Library
25. GRINSPUN, E., HIRANI, A., DESBRUN, M., AND SCHRODER, P. 2003. Discrete shells. In Proc. of the 2003 ACM SIGGRAPH/Eurographics Symp. on Comput. Anim., 62–67. Google ScholarDigital Library
26. HIROTA, K., TANOUE, Y., AND KANEKO, T. 1998. Generation of crack patterns with a physical model. The Vis. Comput. 14, 126–187.Google ScholarCross Ref
27. HIRT, C., AMSDEN, A., AND COOK, J. 1974. An arbitrary Lagrangian-Eulerian computing method for all flow speeds. J. Comput. Phys. 135, 227–253. Google ScholarDigital Library
28. IRVING, G., TERAN, J., AND FEDKIW, R. 2004. Invertible finite elements for robust simulation of large deformation. Submitted to the Symposium on Computer Animation (SCA). Google ScholarDigital Library
29. JAMES, D., AND FATAHALIAN, K. 2003. Precomputing interactive dynamic deformable scenes. ACM Trans. Graph. (SIGGRAPH Proc.) 22, 879–887. Google ScholarDigital Library
30. JAMES, D., AND PAI, D. 2002. DyRT: Dynamic response textures for real time deformation simulation with graphics hardware. ACM Trans. Graph. (SIGGRAPH Proc.) 21, 582–585. Google ScholarDigital Library
31. JIRASEK, M., AND ZIMMERMANN, T. 2001. Embedded crack model: II. combination with smeared cracks. Int. J. Num. Meth. Eng. 50, 1291–1305.Google ScholarCross Ref
32. MAZARAK, O., MARTINS, C., AND AMANATIDES, J. 1999. Animating exploding objects. In Proc. of Graph. Interface 1999, 211–218. Google ScholarDigital Library
33. MOLINO, N., BRIDSON, R., TERAN, J., AND FEDKIW, R. 2003. A crystalline, red green strategy for meshing highly deformable objects with tetrahedra. In 12th Int. Meshing Roundtable, 103–114.Google Scholar
34. MOR, A., AND KANADE, T. 2000. Modifying soft tissue models: progressive cutting with minimal new element creation. In MICCAI, 598–607. Google ScholarDigital Library
35. MULLER, M., AND GROSS, M. 2004. Interactive virtual materials. In Grap. Interface. Google ScholarDigital Library
36. MULLER, M., MCMILLAN, L., DORSEY, J., AND JAGNOW, R. 2001. Real-time simulation of deformation and fracture of stiff materials. In Comput. Anim. and Sim. ’01, Proc. Eurographics Workshop, Eurographics Assoc., 99–111. Google ScholarDigital Library
37. MULLER, M., DORSEY, J., MCMILLAN, L., JAGNOW, R., AND CUTLER, B. 2002. Stable real-time deformations. In ACM SIGGRAPH Symp. on Comput. Anim., 49–54. Google ScholarDigital Library
38. MULLER, M., TESCHNER, M., AND GROSS, M. 2004. Physically-based simulation of objects represented by surface meshes. In Proc. Comput. Graph. Int., 156–165. Google ScholarDigital Library
39. MUSETH, K., BREEN, D., WHITAKER, R., AND BARR, A. 2002. Level set surface editing operators. ACM Trans. Graph. (SIGGRAPH Proc.) 21, 3, 330–338. Google ScholarDigital Library
40. NEFF, M., AND FIUME, E. 1999. A visual model for blast waves and fracture. In Proc. of Graph. Interface 1999, 193–202. Google ScholarDigital Library
41. NORTON, A., TURK, G., BACON, B., GERTH, J., AND SWEENEY, P. 1991. Animation of fracture by physical modeling. Vis. Comput. 7, 4, 210–219. Google ScholarDigital Library
42. O’BRIEN, J., AND HODGINS, J. 1999. Graphical modeling and animation of brittle fracture. In Proc. SIGGRAPH 99, vol. 18, 137–146. Google ScholarDigital Library
43. O’BRIEN, J., BARGTEIL, A., AND HODGINS, J. 2002. Graphical modeling of ductile fracture. ACM Trans. Graph. (SIGGRAPH Proc.) 21, 291–294. Google ScholarDigital Library
44. ORTIZ, M., AND PANDOLFI, A. 1999. Finite-deformation irreversible cohesive elements for three-dimensional crack-propagation analysis. Int. J. Num. Meth. Eng. 44, 1267–1282.Google ScholarCross Ref
45. PERRY, R., AND FRISKEN, S. 2001. Kizamu: a system for sculpting digital characters. In Proc. SIGGRAPH 2001, vol. 20, 47–56. Google ScholarDigital Library
46. RANKINE, W. 1872. Applied mechanics. Charles Griffen and Company, London.Google Scholar
47. SEDERBERG, T., AND PARRY, S. 1986. Free-form deformations of solid geometric models. Comput. Graph. (SIGGRAPH Proc.), 151–160. Google ScholarDigital Library
48. SMITH, J., WITKIN, A., AND BARAFF, D. 2001. Fast and controllable simulation of the shattering of brittle objects. In Comput. Graphics Forum, D. Duke and R. Scopigno, Eds., vol. 20(2). Blackwell Publishing, 81–91.Google Scholar
49. TABIEI, A., AND WU, J. 2003. Development of the DYNA3D simulation code with automated fracture procedure for brick elements. Int. J. Num. Meth. Eng. 57, 1979–2006.Google ScholarCross Ref
50. TERAN, J., SALINAS-BLEMKER, S., NG, V., AND FEDKIW, R. 2003. Finite volume methods for the simulation of skeletal muscle. In Proc. of the 2003 ACM SIGGRAPH/Eurographics Symp. on Comput. Anim., 68–74. Google ScholarDigital Library
51. TERZOPOULOS, D., AND FLEISCHER, K. 1988. Deformable models. The Visual Computer, 4, 306–331.Google ScholarCross Ref
52. TERZOPOULOS, D., AND FLEISCHER, K. 1988. Modeling inelastic deformation: viscoelasticity, plasticity, fracture. Comput. Graph. (SIGGRAPH Proc.), 269–278. Google ScholarDigital Library
53. TERZOPOULOS, D., PLATT, J., BARR, A., AND FLEISCHER, K. 1987. Elastically deformable models. Comput. Graph. (Proc. SIGGRAPH 87) 21, 4, 205–214. Google ScholarDigital Library
54. TREUILLE, A., MCNAMARA, A., POPOVIC, Z., AND STAM, J. 2003. Keyframe control of smoke simulations. ACM Trans. Graph. (SIGGRAPH Proc.) 22, 716–723. Google ScholarDigital Library
55. VENTURA, G., BUDYN, E., AND BELYTSCHKO, T. 2003. Vector level sets for description of propagating cracks in finite elements. Int. J. Num. Meth. Eng. 58, 1571–1592.Google ScholarCross Ref
56. WELLS, G., AND SLUYS, L. 2001. A new method for modelling cohesive cracks using finite elements. Int. J. Num. Meth. Eng. 50, 2667–2682.Google ScholarCross Ref
57. YNGVE, G., O’BRIEN, J., AND HODGINS, J. 2000. Animating explosions. In Proc. SIGGRAPH 2000, vol. 19, 29–36. Google ScholarDigital Library