“A signal processing approach to fair surface design” by Taubin

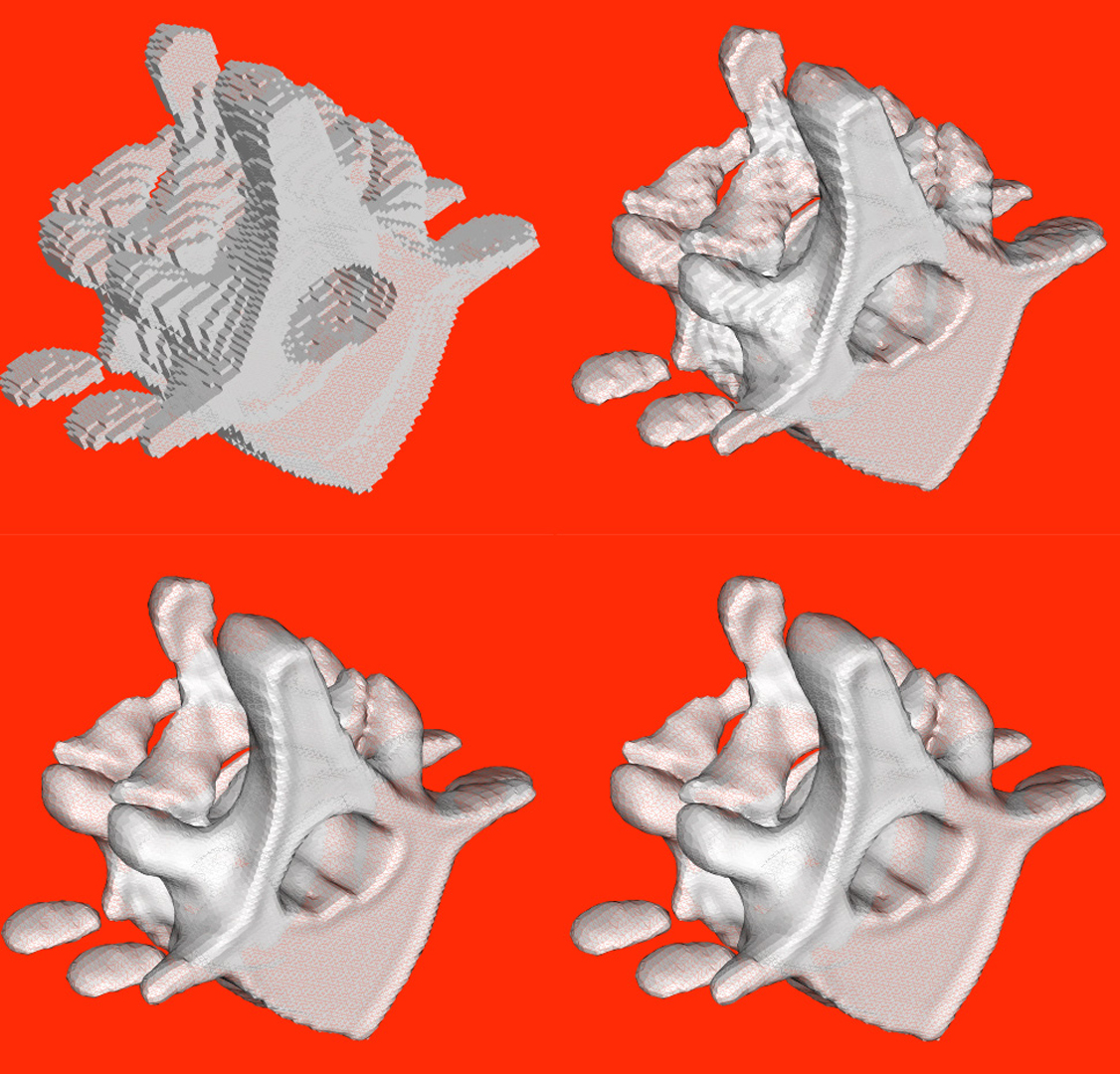
In this paper we describe a new tool for interactive free-form fair surface design. By generalizing classical discrete Fourier analysis to two-dimensional discrete surface signals – functions defined on polyhedral surfaces of arbitrary topology –, we reduce the problem of surface smoothing, or fairing, to low-pass filtering. We describe a very simple surface signal low-pass filter algorithm that applies to surfaces of arbitrary topology. As opposed to other existing optimization-based fairing methods, which are computationally more expensive, this is a linear time and space complexity algorithm. With this algorithm, fairing very large surfaces, such as those obtained from volumetric medical data, becomes affordable. By combining this algorithm with surface subdivision methods we obtain a very effective fair surface design technique. We then extend the analysis, and modify the algorithm accordingly, to accommodate different types of constraints. Some constraints can be imposed without any modification of the algorithm, while others require the solution of a small associated linear system of equations. In particular, vertex location constraints, vertex normal constraints, and surface normal discontinuities across curves embedded in the surface, can be imposed with this technique.

1. C.L. Bajaj and Ibm. Smoothing polyhedra using implicit algebraic splines. Computer Graphics, pages 79-88, July 1992. (Proceedings SIGGRAPH’92).
2. H. Baker. Building surfaces of evolution: The weaving wall. International Journal of Computer Vision, 3:51-71,1989.
3. E Borrel. Simple constrained deformations for geometric modeling and interactive design. ACM Transactions on Graphics, 13(2):137- 155, April 1994.
4. E. Catmull and J. Clark. Recursively generated B-spline surfaces on arbitrary topological meshes. Computer Aided Design, 10:350-355, 1978.
5. G. Celniker and D. Gossard. Deformable curve and surface finiteelements for free-form shape design. Computer Graphics, pages 257- 266, July 1991. (Proceedings SIGGRAPH’91).
6. T.D. DeRose, M. Lounsbery, and J. Warren. Multiresolution analysis for surfaces of arbitrary topological type. Technical Report 93-10- 05, Department of Computer Science and Enginnering, University of Washington, Seattle, 1993.
7. M. Do Carmo. Differential Geometry of Curves and Surfaces. Prentice Hall, 1976.
8. D. Doo and M. Sabin. Behaviour of recursive division surfaces near extraordinary points. Computer Aided Design, 10:356-360, 1978.
9. G. Golub and C.E Van Loan. Matrix Computations. John Hopkins University Press, 2nd. edition, 1989.
10. G. Greiner and H.E Seidel. Modeling with triangular b-splines. IEEE Computer Graphics and Applications, 14(2):56-60, March 1994.
11. A. Gu6ziec and R. Hummel. The wrapper algorithm: Surface extraction and simplification. In IEEE Workshop on Biomedical Image Analysis, pages 204-213, Seattle, WA, June 24-25 1994.
12. M. Halstead, M. Kass, and T. DeRose. Efficient, fair interpolation using catmull-clark surface. Computer Graphics,pages 35-44,August 1993. (Proceedings SIGGRAPH’93).
13. H. Hoppe, T. DeRose, T. Duchamp, J. McDonald, and W. Stuetzle. Mesh optimization. Computer Graphics, pages 19-26, August 1993. (Proceedings SIGGRAPH’93).
14. W.M. Hsu, J.E Hughes, and H. Kaufman. Direct manipulation of freeform deformations. Computer Graphics, pages 177-184, July 1992. (Proceedings SIGGRAPH’92).
15. A.D. Kalvin. Segmentation and Surface-Based Modeling of Objects in Three-Dimensional Biomedical Images. PhD thesis, New York University, New York, March 1991.
16. M. Kass, A. Witkin, and D. Terzopoulos. Snakes: active contour models. International Journal of Computer Vision, 1(4):321-331, 1988.
17. T. Lindeberg. Scale-space for discrete signals. IEEE Transactions on Pattern Analysis and Machine Intelligence, 12(3):234-254, March 1990.
18. C. Loop. Smooth subdivision surfaces based on triangles. Master’s thesis, Dept. of Mathematics, University of Utah, August 1987.
19. C. Loop. A G1 triangular spline surface of arbitrary topological type. Computer Aided Geometric Design, 11:303-330, 1994.
20. C. Loop. Smooth spline surfaces over irregular meshes. Computer Graphics, pages 303-310, July 1994. (Proceedings SIGGRAPH’94).
21. W. Lorenson and H. Cline. Marching cubes: A high resolution 3d surface construction algorithm. Computer Graphics, pages 163-169, July 1987. (Proceedings SIGGRAPH).
22. M. Lounsbery, S. Mann, and T. DeRose. Parametric surface interpolation. IEEE Computer Graphics and Applications, 12(5):45-52, September 1992.
23. J. Menon. Constructive shell representations for freeform surfaces and solids. IEEE Computer Graphics and Applications, 14(2):24-36, March 1994.
24. H.E Moreton and C.H. S6quin. Functional optimization for fair surface design. Computer Graphics, pages 167-176, July 1992. (Proceedings SIGGRAPH’92).
25. J. Oliensis. Local reproducible smoothing without shrinkage. IEEE Transactions on Pattern Analysis and Machine Intelligence, 15(3):307-312, March 1993.
26. A. Pentland and S. Sclaroff. Closed-form solutions for physically based shape modeling and recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, 13(7):715-729, July 1991.
27. E. Seneta. Non-Negative Matrices, An Introduction to Theory and Applications. John Wiley & Sons, New York, 1973.
28. L.A. Shirman and C.H. S6quin. Local surface interpolation with bezier patches. Computer Aided Geometric Design, 4:279-295, 1987.
29. W.J. Shroeder, A. Zarge, and W.E. Lorensen. Decimation of triangle meshes. Computer Graphics, pages 65-70, 1992. (Proceedings SIGGRAPH’92).
30. R.S. Szeliski, D. Tonnesen, and D. Terzopoulos. Modeling surfaces of arbitrary topology with dynamic particles. In Proceedings, IEEE Conference on Computer Vision and Pattern Recognition, pages 82- 87, New York, NY, June 15-17 1993.
31. G. Taubin. Curve and surface smoothing without shrinkage. Technical Report RC-19536, IBM Research, April 1994. (also in Proceedings ICCV’95).
32. G. Taubin. Estimating the tensor of curvature of a surface from a polyhedral approximation. Technical Report RC-19860, IBM Research, December 1994. (also in Proceedings ICCV’95).
33. G. Taubin, T. Zhang, and G. Golub. Optimal polyhedral surface smoothing as filter design. (in preparation).
34. D. Terzopoulos and K. Fleischer. Deformable models. The Visual Computer, 4:306-311,1988.
35. G. Turk. Re-filing polygonal surfaces. Computer Graphics, pages 55-64, July 1992. (Proceedings SIGGRAPH’92).
36. G. Turk and M. Levoy. Zippered polygon meshes from range data. Computer Graphics, pages 311-318, July 1994. (Proceedings SIG- GRAPH’94).
37. W. Welch and A. Witkin. Variational surface modeling. Computer Graphics, pages 157-166, July 1992. (Proceedings SIGGRAPH’92).
38. W. Welch and A. Witkin. Free-form shape design using triangulated surfaces. Computer Graphics, pages 247-256, July 1994. (Proceedings SIGGRAPH’94).
39. A.E Witkin. Scale-space filtering. In Proceedings, 8th. International Joint Conference on Artificial Intelligence (IJCAI), pages 1019-1022, Karlsruhe, Germany, August 1983.
40. C.T. Zahn and R.Z. Roskies. Fourier descriptors for plane closed curves. IEEE Transactions on Computers, 21(3):269-281, March 1972.