“A Fast and Robust Solution for Cubic and Higher-order Polynomials” by Yuksel
Conference:
Type(s):
Entry Number: 28
Title:
- A Fast and Robust Solution for Cubic and Higher-order Polynomials
Presenter(s)/Author(s):
Abstract:
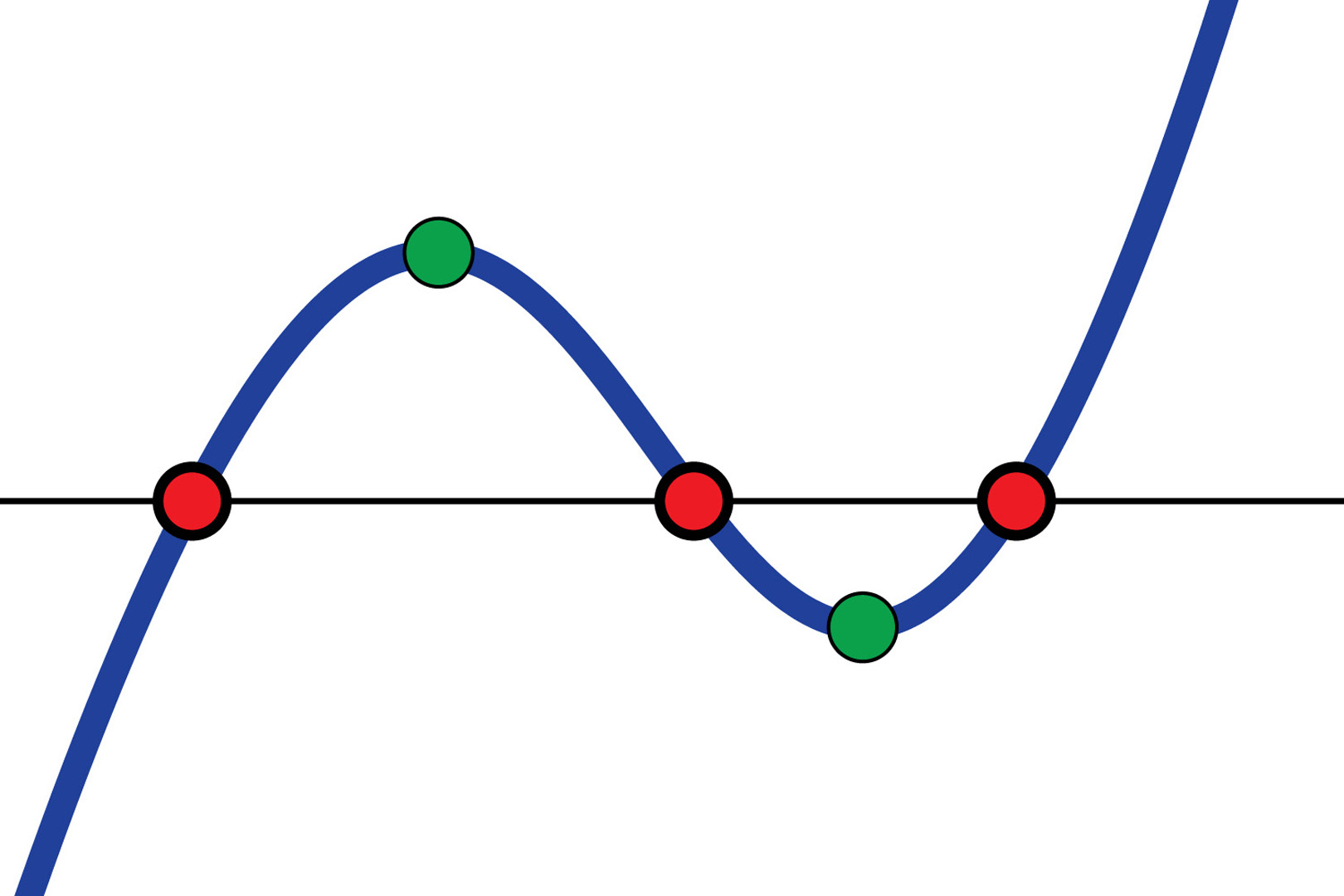
We present a computationally-efficient and numerically-robust method for finding real roots of cubic and higher-order polynomials. It begins with determining the intervals where a given polynomial is monotonic. Then, the existence of a real root within each interval can be quickly identified. If one exists, we find the root using a stable variant of Newton iterations, providing fast and guaranteed convergence and satisfying the given error bound.
References:
Gaël Guennebaud, Benoît Jacob, 2010. Eigen v3. http://eigen.tuxfamily.org.Google Scholar
M. A. Jenkins and J. F. Traub. 1970. A Three-Stage Algorithm for Real Polynomials Using Quadratic Iteration. SIAM J. Numer. Anal. 7, 4 (1970), 545–566.Google ScholarDigital Library
Cem Yuksel. 2022. Polynomial Roots. http://www.cemyuksel.com/?x=polynomials.Google Scholar