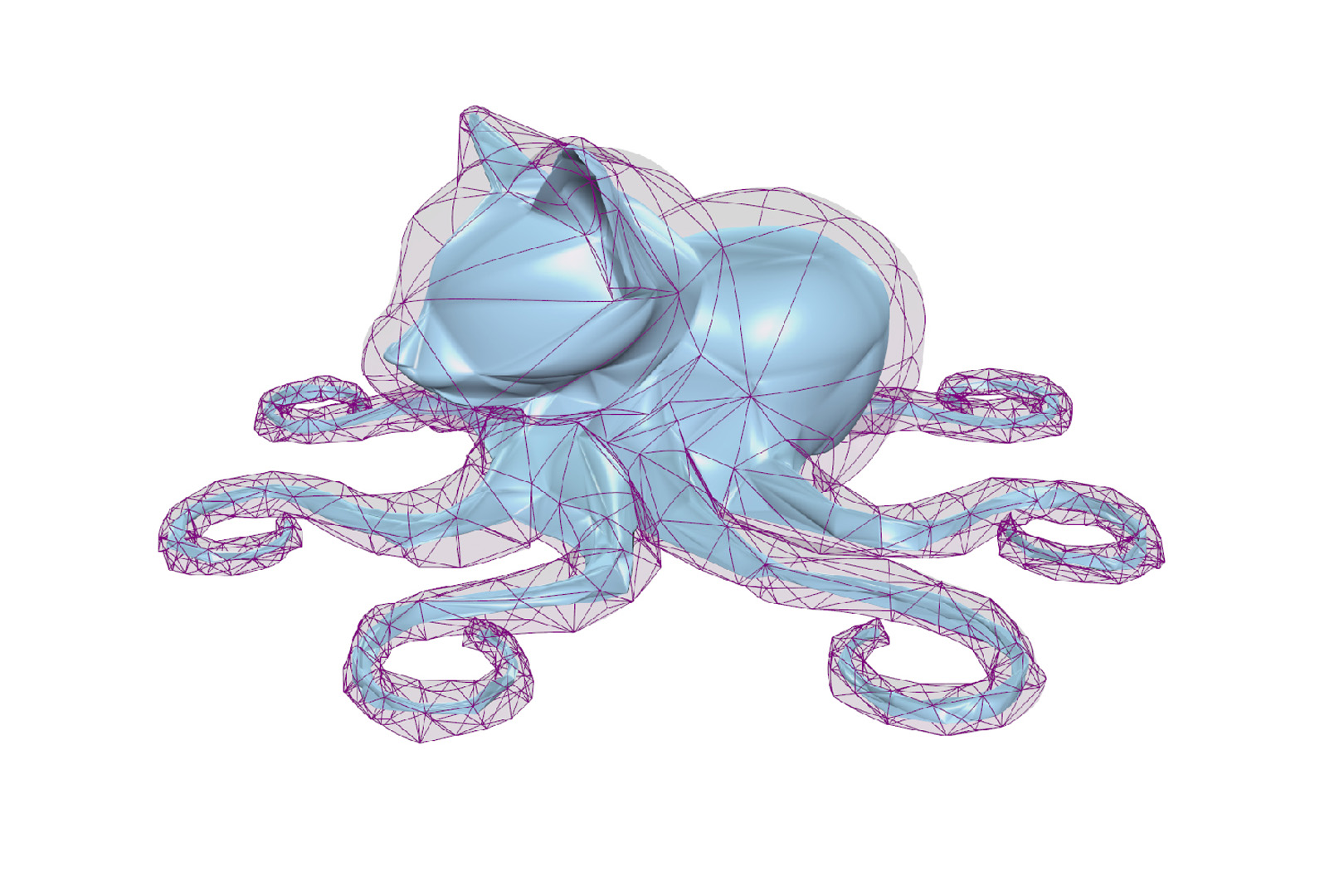
“Smooth Bijective Projection in a High-order Shell”
Conference:
Type(s):
Title:
- Smooth Bijective Projection in a High-order Shell
Presenter(s)/Author(s):
Abstract:
We propose a new high-order shell structure for the smooth attribute transfer between meshes inside the shell, along with a robust construction algorithm. The high-order shell is enveloped by three B\'{e}zier triangles and three side surfaces, with a smooth bijective projection inside.
References:
[1]
Noam Aigerman, Shahar Z Kovalsky, and Yaron Lipman. 2017. Spherical orbifold tu e embeddings. ACM Trans. Graph. 36, 4 (2017), 90.
[2]
R Aubry, S Dey, EL Mestreau, and BK Karamete. 2017. Boundary layer mesh generation on arbitrary geometries. Internat. J. Numer. Methods Engrg. 112, 2 (2017), 157–173.
[3]
St?phane Calderon and Tamy Boubekeur. 2017. Bounding proxies for shape approximation. ACM Trans. Graph. 36, 4 (2017), 57–1.
[4]
Yanyun Chen, Xin Tong, Jiaping Wang, Stephen Lin, Baining Guo, and Heung-Yeung Shum. 2004. Shell texture functions. ACM Trans. Graph. 23, 3 (2004), 343–353.
[5]
Xiao-Xiang Cheng, Xiao-Ming Fu, Chi Zhang, and Shuangming Chai. 2019. Practical error-bounded remeshing by adaptive refinement. Computers & Graphics 82 (2019), 163–173.
[6]
Philippe G. Ciarlet. 1991. Basic error estimates for elliptic problems. Handbook of Numerical Analysis 2 (1991), 17–351.
[7]
Jonathan Cohen, Dinesh Manocha, and Marc Olano. 1997. Simplifying polygonal models using successive mappings. In Proceedings. Visualization’97 (Cat. No. 97CB36155). IEEE, 395–402.
[8]
Keenan Crane, Clarisse Weischedel, and Max Wardetzky. 2012. Geodesics in heat: A new approach to computing distance based on heat flow. ArXiv abs/1204.6216 (2012).
[9]
Swagatam Das and Ponnuthurai Nagaratnam Suganthan. 2011. Differential Evolution: A Survey of the State-of-the-Art. IEEE Transactions on Evolutionary Computation 15, 1 (2011), 4–31.
[10]
Saikat Dey, Robert M. O’Bara, and Mark S. Shephard. 1999. Curvilinear mesh generation in 3D. In Proceedings of the 8th International Meshing Roundtable. 407–417.
[11]
Danielle Ezuz, Justin Solomon, and Mirela Ben-Chen. 2019. Reversible harmonic maps between discrete surfaces. ACM Trans. Graph. 38, 2 (2019), 1–12.
[12]
Gerald Farin. 1986. Triangular Bernstein-B?zier patches. Comput. Aided Geom. Des. 3, 2 (1986), 83–127.
[13]
Zachary Ferguson, Pranav Jain, Denis Zorin, Teseo Schneider, and Daniele Panozzo. 2023. High-Order Incremental Potential Contact for Elastodynamic Simulation on Curved Meshes. ACM SIGGRAPH 2023 Conference Proceedings (2023).
[14]
Michael S Floater. 1997. Parametrization and smooth approximation of surface triangulations. Computer aided geometric design 14, 3 (1997), 231–250.
[15]
Rao V Garimella and Mark S Shephard. 2000. Boundary layer mesh generation for viscous flow simulations. Internat. J. Numer. Methods Engrg. 49, 1–2 (2000), 193–218.
[16]
Michael Garland and Paul S Heckbert. 1997. Surface simplification using quadric error metrics. In Proceedings of the 24th annual conference on Computer graphics and interactive techniques. 209–216.
[17]
Kai Hormann, Bruno L?vy, and Alla Sheffer. 2007. Mesh parameterization: Theory and practice. (2007).
[18]
Kai Hormann and N Sukumar. 2017. Generalized barycentric coordinates in computer graphics and computational mechanics. CRC press.
[19]
Yixin Hu, Teseo Schneider, Xifeng Gao, Qingnan Zhou, Alec Jacobson, Denis Zorin, and Daniele Panozzo. 2019. TriWild: robust triangulation with curve constraints. ACM Trans. Graph. 38, 4 (2019).
[20]
Yixin Hu, Teseo Schneider, Bolun Wang, Denis Zorin, and Daniele Panozzo. 2020. Fast tetrahedral meshing in the wild. ACM Trans. Graph. 39, 4 (2020), 117–1.
[21]
Zhongshi Jiang, Scott Schaefer, and Daniele Panozzo. 2017. Simplicial complex augmentation framework for bijective maps. ACM Trans. Graph. 36, 6 (2017).
[22]
Zhongshi Jiang, Teseo Schneider, Denis Zorin, and Daniele Panozzo. 2020. Bijective projection in a shell. ACM Trans. Graph. 39 (2020), 1–18.
[23]
Zhongshi Jiang, Ziyi Zhang, Yixin Hu, Teseo Schneider, Denis Zorin, and Daniele Panozzo. 2021. Bijective and coarse high-order tetrahedral meshes. ACM Trans. Graph. (2021).
[24]
Xiangmin Jiao and Michael T. Heath. 2004. Overlaying Surface Meshes, Part I: Algorithms. International Journal of Computational Geometry and Applications 14, 379–402.
[25]
Miao Jin, Junho Kim, Feng Luo, and Xianfeng Gu. 2008. Discrete surface Ricci flow. IEEE Transactions on Visualization and Computer Graphics 14, 5 (2008), 1030–1043.
[26]
Yao Jin, Dan Song, Tongtong Wang, Jin Huang, Ying Song, and Lili He. 2019. A shell space constrained approach for curve design on surface meshes. Computer-Aided Design 113 (2019), 24–34.
[27]
Payam Khanteimouri and Marcel Campen. 2023. 3D B?zier Guarding: Boundary-Conforming Curved Tetrahedral Meshing. ACM Trans. Graph. 42, 6 (2023).
[28]
Liliya Kharevych, Boris Springborn, and Peter Schr?der. 2006. Discrete conformal mappings via circle patterns. ACM Trans. Graph. 25, 2 (2006), 412–438.
[29]
Peter Knabner and Gerhard Summ. 2001. The invertibility of the isoparametric mapping for pyramidal and prismatic finite elements. Numer. Math. 88 (2001), 661–681.
[30]
Felix Kn?ppel, Keenan Crane, Ulrich Pinkall, and Peter Schr?der. 2013. Globally optimal direction fields. ACM Trans. Graph. 32, 4 (2013).
[31]
Leif Kobbelt, Swen Campagna, Jens Vorsatz, and Hans-Peter Seidel. 1998. Interactive multi-resolution modeling on arbitrary meshes. Proceedings of the 25th annual conference on Computer graphics and interactive techniques (1998).
[32]
Sebastian Koch, Albert Matveev, Zhongshi Jiang, Francis Williams, Alexey Artemov, Evgeny Burnaev, Marc Alexa, Denis Zorin, and Daniele Panozzo. 2018. ABC: A Big CAD Model Dataset for Geometric Deep Learning. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (2018), 9593–9603.
[33]
Vladislav Kraevoy and Alla Sheffer. 2004. Cross-parameterization and compatible remeshing of 3D models. ACM Trans. Graph. (2004), 861–869.
[34]
Aaron Lee, Henry Moreton, and Hugues Hoppe. 2000. Displaced subdivision surfaces. In Proceedings of the 27th annual conference on Computer graphics and interactive techniques. 85–94.
[35]
Aaron W. F. Lee, Wim Sweldens, Peter Schr?der, Lawrence C. Cowsar, and David P. Dobkin. 1998. MAPS: multiresolution adaptive parameterization of surfaces. Proceedings of the 25th annual conference on Computer graphics and interactive techniques (1998).
[36]
Jerome Lengyel, Emil Praun, Adam Finkelstein, and Hugues Hoppe. 2001. Real-time fur over arbitrary surfaces. In Proceedings of the 2001 symposium on Interactive 3D graphics. 227–232.
[37]
Hsueh-Ti Derek Liu, Mark Gillespie, Benjamin Chislett, Nicholas Sharp, Alec Jacobson, and Keenan Crane. 2023. Surface Simplification using Intrinsic Error Metrics. ACM Trans. Graph. 42 (2023), 1–17.
[38]
Hsueh-Ti Derek Liu, Vladimir G. Kim, Siddhartha Chaudhuri, Noam Aigerman, and Alec Jacobson. 2020. Neural subdivision. ACM Trans. Graph. 39 (2020), 124:1–124:16.
[39]
Hsueh-Ti Derek Liu, Jiayi Eris Zhang, Mirela Ben-Chen, and Alec Jacobson. 2021b. Surface multigrid via intrinsic prolongation. ACM Trans. Graph. 40 (2021), 1–13.
[40]
Zhong-Yuan Liu, Jian-Ping Su, Hao Liu, Chunyang Ye, Ligang Liu, and Xiao-Ming Fu. 2021a. Error-bounded Edge-based Remeshing of High-order Tetrahedral Meshes. Comput. Aided Des. 139 (2021), 103080.
[41]
Andrea Maggiordomo, Yury Uralsky, Henry P. Moreton, and Marco Tarini. 2023. The inverse barycentric displacement problem. The Visual Computer (2023).
[42]
Manish Mandad and Marcel Campen. 2020. B?zier guarding: precise higher-order meshing of curved 2D domains. ACM Trans. Graph. 39, 4 (2020), 103:1–103:15.
[43]
Joseph SB Mitchell, David M Mount, and Christos H Papadimitriou. 1987. The discrete geodesic problem. SIAM J. Comput. 16, 4 (1987), 647–668.
[44]
Ferrante Neri and Ville Tirronen. 2010. Recent advances in differential evolution: a survey and experimental analysis. Artif. Intell. Rev. 33 (2010), 61–106.
[45]
Maks Ovsjanikov, Mirela Ben-Chen, Justin Solomon, Adrian Butscher, and Leonidas Guibas. 2012. Functional maps: a flexible representation of maps between shapes. ACM Trans. Graph. (2012), 1–11.
[46]
Daniele Panozzo, Ilya Baran, Olga Diamanti, and Olga Sorkine-Hornung. 2013. Weighted averages on surfaces. ACM Trans. Graph. 32, 4 (2013), 1–12.
[47]
Jianbo Peng, Daniel Kristjansson, and Denis Zorin. 2004. Interactive modeling of topologically complex geometric detail. In ACM SIGGRAPH 2004 Papers. 635–643.
[48]
Nico Pietroni, Marco Tarini, and Paolo Cignoni. 2009. Almost isometric mesh parameterization through abstract domains. IEEE Transactions on Visualization and Computer Graphics 16, 4 (2009), 621–635.
[49]
Serban D Porumbescu, Brian Budge, Louis Feng, and Kenneth I Joy. 2005. Shell maps. ACM Trans. Graph. 24, 3 (2005), 626–633.
[50]
Emil Praun, Wim Sweldens, and Peter Schr?der. 2001. Consistent mesh parameterizations. In Proceedings of the 28th annual conference on Computer graphics and interactive techniques. 179–184.
[51]
Eloi Ruiz-Giron?s, Josep Sarrate, and Xevi Roca. 2021. Measuring and improving the geometric accuracy of piece-wise polynomial boundary meshes. J. Comput. Phys. (oct 2021), 22 pages.
[52]
Johnathan Richard Shewchuk. 1996. Robust Adaptive Floating-Point Geometric Predicates. Association for Computing Machinery, 141–150.
[53]
Jonathan Richard Shewchuk. 1997. Adaptive Precision Floating-Point Arithmetic and Fast Robust Geometric Predicates. Discrete & Computational Geometry 18, 3 (1997), 305–363.
[54]
Meged Shoham, Amir Vaxman, and Mirela Ben-Chen. 2019. Hierarchical functional maps between subdivision surfaces. In Computer Graphics Forum, Vol. 38. Wiley Online Library, 55–73.
[55]
Vitaly Surazhsky and Craig Gotsman. 2001. Morphing stick figures using optimized compatible triangulations. In Proceedings Ninth Pacific Conference on Computer Graphics and Applications. Pacific Graphics 2001. IEEE, 40–49.
[56]
Jean-Marc Thiery, Julien Tierny, and Tamy Boubekeur. 2012. CageR: cage-based reverse engineering of animated 3D shapes. In Computer Graphics Forum, Vol. 31. Wiley Online Library, 2303–2316.
[57]
William Thomas Tutte. 1963. How to draw a graph. Proceedings of the London Mathematical Society 3, 1 (1963), 743–767.
[58]
Lifeng Wang, Xi Wang, Xin Tong, Stephen Lin, Shimin Hu, Baining Guo, and Heung-Yeung Shum. 2003. View-dependent displacement mapping. ACM Trans. Graph. 22, 3 (2003), 334–339.
[59]
Xi Wang, Xin Tong, Stephen Lin, Shimin Hu, Baining Guo, and Heung-Yeung Shum. 2004. Generalized displacement maps. In Eurographics Symposium on Rendering (EGSR). 227–233.
[60]
Jing Xu and Andrey N. Chernikov. 2014. Automatic curvilinear quality mesh generation driven by smooth boundary and guaranteed fidelity. Procedia Engineering 82 (2014), 200–212.
[61]
Wen-Xiang Zhang, Qi Wang, Jianzhi Guo, Shuangming Chai, Ligang Liu, and Xiao-Ming Fu. 2022. Constrained Remeshing Using Evolutionary Vertex Optimization. Comput. Graph. Forum 41 (2022).
[62]
Qingnan Zhou and Alec Jacobson. 2016. Thingi10K: A Dataset of 10,000 3D-Printing Models. ArXiv abs/1605.04797 (2016).