“GPU-efficient recursive filtering and summed-area tables”
Conference:
Type(s):
Title:
- GPU-efficient recursive filtering and summed-area tables
Session/Category Title:
- Image Processing
Presenter(s)/Author(s):
Abstract:
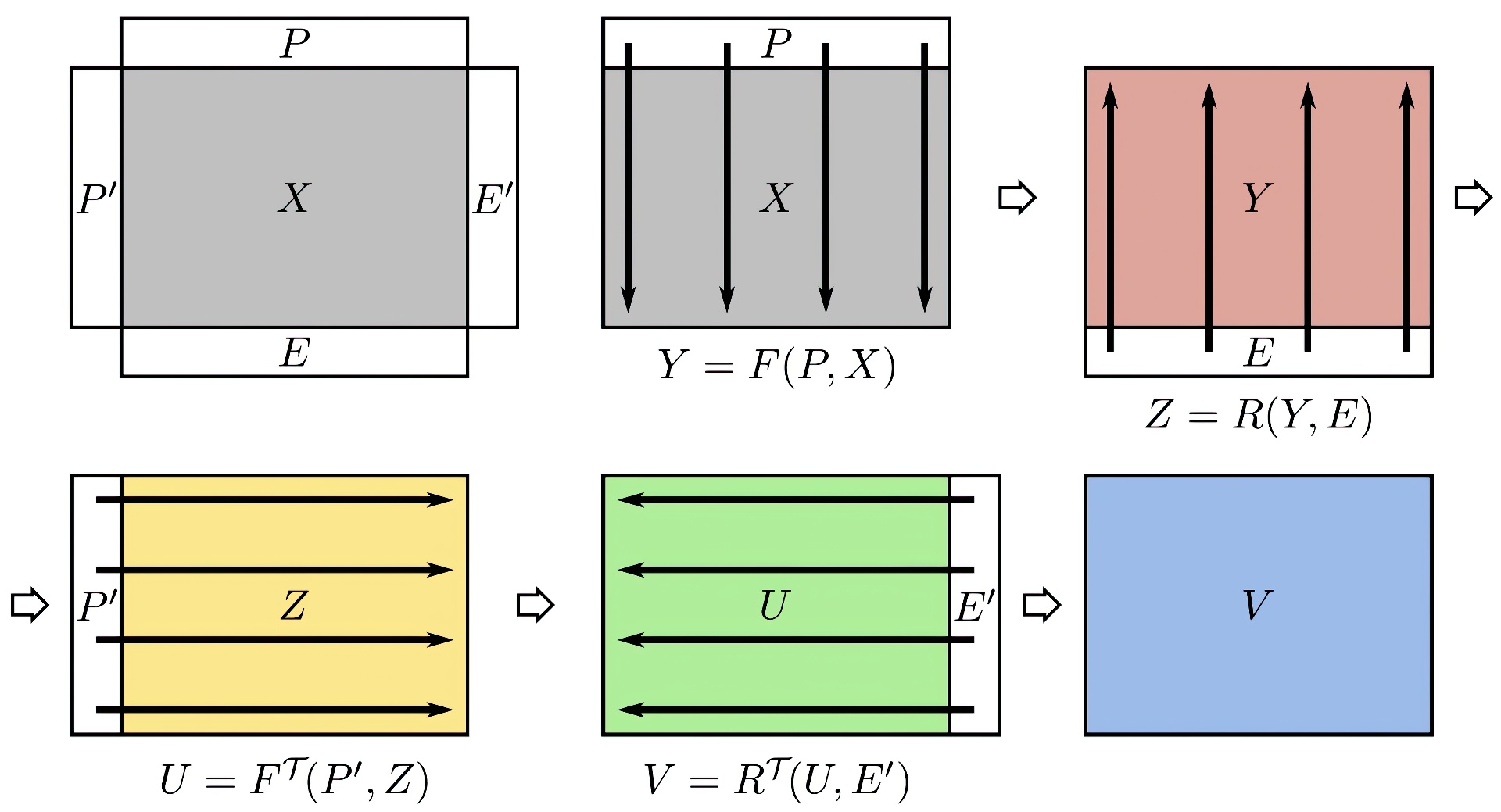
Image processing operations like blurring, inverse convolution, and summed-area tables are often computed efficiently as a sequence of 1D recursive filters. While much research has explored parallel recursive filtering, prior techniques do not optimize across the entire filter sequence. Typically, a separate filter (or often a causal-anticausal filter pair) is required in each dimension. Computing these filter passes independently results in significant traffic to global memory, creating a bottleneck in GPU systems. We present a new algorithmic framework for parallel evaluation. It partitions the image into 2D blocks, with a small band of additional data buffered along each block perimeter. We show that these perimeter bands are sufficient to accumulate the effects of the successive filters. A remarkable result is that the image data is read only twice and written just once, independent of image size, and thus total memory bandwidth is reduced even compared to the traditional serial algorithm. We demonstrate significant speedups in GPU computation.
References:
1. Blelloch, G. E. 1989. Scans as primitive parallel operations. IEEE Transactions on Computers, 38(11). Google ScholarDigital Library
2. Blelloch, G. E. 1990. Prefix sums and their applications. Technical Report CMU-CS-90-190, Carnegie Mellon University.Google Scholar
3. Blu, T., Thénavaz, P., and Unser, M. 1999. Generalized interpolation: Higher quality at no additional cost. In IEEE International Conference on Image Processing, volume 3, 667–671.Google Scholar
4. Blu, T., Thévenaz, P., and Unser, M. 2001. MOMS: Maximalorder interpolation of minimal support. IEEE Transactions on Image Processing, 10(7):1069–1080. Google ScholarDigital Library
5. Crow, F. 1984. Summed-area tables for texture mapping. In Computer Graphics (Proceedings of ACM SIGGRAPH 90), volume 18, ACM, 207–212. Google ScholarDigital Library
6. CUDPP library. 2011. URL http://code.google.com/p/cudpp/.Google Scholar
7. CUFFT library. 2007. URL http://developer.nvidia.com/cuda-toolkit. NVIDIA Corporation.Google Scholar
8. Deriche, R. 1992. Recursively implementing the Gaussian and its derivatives. In Proceedings of the 2
nd Conference on Image Processing, 263–267.Google Scholar
9. Dotsenko, Y., Govindaraju, N. K., Sloan, P.-P., Boyd, C., and Manferdelli, J. 2008. Fast scan algorithms on graphics processors. In Proceedings of the 22
nd Annual International Conference on Supercomputing, 205–213. Google ScholarDigital Library
10. Göddeke, D. and Strzodka, R. 2011. Cyclic reduction tridiagonal solvers on GPUs applied to mixed-precision multigrid. IEEE Transactions on Parallel and Distributed Systems, 22(1):22–32. Google ScholarDigital Library
11. Harris, M., Sengupta, S., and Owens, J. D. 2008. Parallel prefix sum (scan) with CUDA. In GPU Gems 3, chapter 39.Google Scholar
12. Hensley, J. 2010. Advanced rendering technique with DirectX 11: High-quality depth of field. Gamefest 2010 talk.Google Scholar
13. Hensley, J., Scheuermann, T., Coombe, G., Singh, M., and Lastra, A. 2005. Fast summed-area table generation and its applications. Computer Graphics Forum, 24(3):547–555.Google ScholarCross Ref
14. Hockney, R. W. and Jesshope, C. R. 1981. Parallel Computers: Architecture, Programming and Algorithms. Adam Hilger. Google ScholarDigital Library
15. Iverson, K. E. 1962. A Programming Language. Wiley. Google ScholarDigital Library
16. Kass, M., Lefohn, A., and Owens, J. D. 2006. Interactive depth of field using simulated diffusion on a GPU. Technical Report #06-01, Pixar Animation Studios.Google Scholar
17. Kirk, D. B. and Hwu, W. W. 2010. Programming Massively Parallel Processors. Morgan Kaufmann. Google ScholarDigital Library
18. Kooge, P. M. and Stone, H. S. 1973. A parallel algorithm for the efficient solution of a general class of recurrence equations. IEEE Transactions on Computers, C-22(8):786–793. Google ScholarDigital Library
19. Lamas-Rodrígues, J., Heras, D. B., Bóo, M., and Argüello, F. 2011. Tridiagonal solvers internal report. Technical report, University of Santiago de Compostela.Google Scholar
20. Merrill, D. and Grimshaw, A. 2009. Parallel scan for stream architectures. Technical Report CS2009-14, University of Virginia.Google Scholar
21. Oppenheim, A. V. and Schafer, R. W. 2010. Discrete-Time Signal Processing. Prentice Hall, 3rd edition. Google ScholarDigital Library
22. Parhi, K. and Messerschmitt, D. 1989. Pipeline interleaving and parallelism in recursive digital filters–Part II: Pipelined incremental block filtering. IEEE Transactions on Acoustics, Speech and Signal Processing, 37(7):1099–1117.Google ScholarCross Ref
23. Podlozhnyuk, V. 2007. Image convolution with CUDA. NVIDIA whitepaper.Google Scholar
24. Ruijters, D. and Thévenaz, P. 2010. GPU prefilter for accurate cubic B-spline interpolation. The Computer Journal. Google ScholarDigital Library
25. Sengupta, S., Harris, M., Zhang, Y., and Owens, J. D. 2007. Scan primitives for GPU computing. In Proceedings of Graphics Hardware, 97–106. Google ScholarDigital Library
26. Stone, H. S. 1971. Parallel processing with the perfect shuffle. IEEE Transactions on Computers, C-20(2):153–161. Google ScholarDigital Library
27. Stone, H. S. 1973. An efficient parallel algorithm for the solution of a tridiagonal linear system of equations. Journal of the ACM, 20(1):27–38. Google ScholarDigital Library
28. Sung, W. and Mitra, S. 1986. Efficient multi-processor implementation of recursive digital filters. In IEEE International Conference on Acoustics, Speech and Signal Processing, 257–260.Google Scholar
29. Sung, W. and Mitra, S. 1992. Multiprocessor implementation of digital filtering algorithms using a parallel block processing method. IEEE Transactions on Parallel and Distributed Systems, 3(1):110–120. Google ScholarDigital Library
30. van Vliet, L. J., Young, I. T., and Verbeek, P. W. 1998. Recursive Gaussian derivative filters. In Proceedings of the 14
th International Conference on Pattern Recognition, 509–514 (v. 1). Google ScholarDigital Library
31. Zhang, Y., Cohen, J., and Owens, J. D. 2010. Fast tridiagonal solvers on the GPU. In Proceedings of the 15
th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming. Google ScholarDigital Library